Описание экспериментальной установки

Прибор для изучения зависимости момента инерции от массы и от распределения ее относительно оси вращения состоит из кронштейна, в подшипниках которого установлена ось испытуемого тела. На нее насажен блок цилиндрической формы с четырьмя взаимно-перпендикулярными стержнями. По стержням можно перемещать шары, благодаря чему можно изменять момент инерции испытуемого тела. На блок наматывается нить. Под действием груза, прикрепленного к концу нити, маховик приводится в равноускоренное вращение. Трение оси в подшипниках незначительно.

При вращении маховика на него действуют момент М силы натяже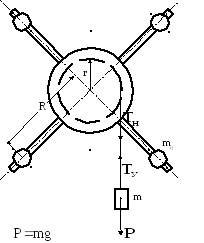ния нити и моментсилы трения, тормозящий вращение. Уравнение движения маховика записывается в виде:

(7)

где – угловое ускорение маховика, J – его момент инерции. Полный момент сил, действующих на маховик, можно считать постоянным, поэтому вращение маховика будет равноускоренным.

Момент силы натяжения нити, приложенный к блоку маховика , где r – радиус блока. Сила натяжения F нити находится из формулы второго закона Ньютона для опускающегося груза. Под действием силы тяжести Р и силы натяжения F, направленной вертикально вверх, груз опускается равноускоренно, так что, где m – масса груза, а –его ускорение. Отсюда сила натяжения нити равна, а момент силы

, (8)

где g – ускорение свободного падения.

Момент силы трения можно найти исходя из следующих соображений. Как только опускающийся на нити груз коснется опоры, нить с грузом соскальзывает с блока маховика, и дальнейшее вращение маховика происходит при действии только тормозящего момента силы трения, и уравнение движения маховика (7) теперь запишется так:

(9)

или

, (10)

где – максимальная угловая скорость маховика,– угловое ускорение маховика,– время вращения маховика после прекращения действия момента силы натяжения нити.

Угловую скорость выразим через касательное ускорение точек на ободе вала:

(11)

где t – время движения опускающегося груза. Касательное ускорение равно ускорению опускающегося груза а, т.е. , следовательно,

(12)

где h- высота, с которой опускается груз. Согласно уравнениям (11) и (12) угловую скорость можно выразить следующим образом:

. (13)

Угловое ускорение маховика при действии момента сил равно

. (14)

Подставив (13) в (10), найдем момент силы трения

. (15)

Подставив (13) в (8), получим выражение для момента силы натяжения нити:

. (16)

Уравнение движения маховика (7) с учетом (12), (15), (16) принимает вид:

, (17)

откуда момент инерции

. (18)

Формула (18) является расчетной для определения момента инерции маховика в данной работе.

Момент инерции маховика относительно оси вращения равен сумме моментов инерции блока и стержней и моментов инерции шаров на стержнях:

, (19)

где – момент инерции блока и стержней, когда грузы сняты со стержней,– момент инерции одного из грузов относительно оси вращения (все шары имеют одинаковые массы и располагаются симметрично на стержнях).

По теореме Штейнера момент инерции можно представить в виде:

, (20)

где – момент инерции шара относительно оси, параллельной оси вращения и проходящей через центр тяжести шара,– масса шара, R – расстояние от центра тяжести шара до оси вращения. Так как, то величинойможно пренебречь, и момент инерции маховика с шарами относительно оси вращения запишется так:

(21)

или

, (22)

откуда

. (23)

Из (23) следует, что момент инерции шаров определяется разностью нагруженного и ненагруженного маховика относительно оси вращения. Моменты инерции J и определяются из опыта.