Lections_V

Уравнение 2t3 + t(1− 2y) − x = 0 есть уравнение нормали к параболе y = x2 − b в точке (t, t2). Если заменить b и а на y и x, то перейдем к уравнению (6.20).

Мы приходим к тривиальному выводу, что центр тяжести (а, b) в положении равновесия должен располагаться непосредственно над точкой касания. Пересечем по- верхность (6.20) рис.6.10 плоскостью b = b0. Получим кубическую кривую:

2t3 − t(1− 2b0 ) − a = 0 .

Если рассматривать а как функцию t, то эта функция имеет максимум и минимум – точку перегиба при b0 = ½. То есть поверхность имеет складку.

Уравнение (6.20) может иметь 1,2 и 3 решения. Число решений зависит от координат (а, b). Каждое решение отвечает положению равновесия качалки. Наша поверхность

Р и с . 6 . 10 . С б о р к а У и тн и в п р о с тр а н с тв е и в п р о е к ц и и н а п ло с ко с ть .

катастроф делит пространство (t, a, b) на две области: в области выше поверхности, мы имеем U(t) > 0, в другой U(t) < 0. Минимум потенциальной энергии достигается при тех значениях t, где функция U(t) меняет знак с минуса на плюс.

Когда U(t) = 0 имеем одно решение – это минимум; когда решений три – одно из них максимум, а два других минимума. Два решения соответствуют: в одной из точек по- верхности (6.20) имеет вертикальную касательную плоскость. Это решение ни макси- мум ни минимум, т.е. V`(t) не меняет знака, а второе решение – минимум. Внутренняя часть складки дает только максимум. Найдем условие, при котором U(t) = 0 имеет кратный корень. Это условие состоит в том, что U(t) =U`(t) = 0, т.е.:

2t3 + t(1− 2b) + a = 0

Отметим, что значения а = 0, b = ½ играют особую роль. Они дают трехкратный ко- рень. В этом случае U(t) = t3 и t = 0 – корень кратности 3. Кривая (6.23) – полукубиче- ская парабола на (a, b) – плоскости, т.е. в пространстве управления, а множество точек

этой кривой называется бифуркационным множеством функции V. Эта кривая отделя- ет точки, дающие одно решение уравнения U(t) = 0 от точек, дающих три решения. Если смотреть на поверхность (6.20) сверху (проекция поверхности на плоскость аb), то видимый контур, вдоль которого перегибается поверхность даст прямую, аналогич-

ную (2.23) рис.6.10.

Посмотрим на это с другой точки зрения.

Мы уже говорили, что (7.22 а) есть уравнение нормали к параболе b = a2 в точке (t, t2). Когда t меняется, а а и b – фиксированы, получаем семейство нормалей. Огибающая этого семейства – эволюта, находится из уравнения (6.22). Т.е. уравнение эволюты есть (6.23).Для заданного положения центра тяжести (а, b) мы имеем уравнение (6.23), определяющее число положений устойчивого равновесия. Будем изменять координаты центра масс, и будем интересоваться не динамикой качалки, а состоянием устойчивого равновесия рис.6.11. В точке 1 – только одно положение устойчивого равновесия. В точке 2 и 3 имеется два положения равновесия. Пока положение равновесия медленно меняет положение параболы. Однако в точке 4 уже не возможно непрерывное измене- ние положения параболы. Малый сдвиг точки вызывает сильное изменение положений равновесия. Происходит катастрофа.

Р и с .6 .1 1 .

Вопрос №61

Геометрическая каустика точечного источника, помещенного в прозрачную среду. Понятие структурной устойчивости каустик.

ченный вращением клюва вокруг оси z. Посмотрим, так ли это? Забегая вперёд, скажу, что это предположение ошибочное!

Пусть теперь уравнение луча, приходящего в точку Р зависит от третьей коорди- наты y, и пусть направление распространения луча определяется ещё и азимутальным углом β в дополнении к полярному углу i.

Тогда вместо уравнения (6.16) получаем:

Можно доказать, что в общем случае условие для огибающей поверхности есть требо-

Второй множитель в уравнении (6.27) задает уравнение поверхности вращения клюва,

а первый множитель x2 + y2 = 0 при х = у

= 0 и z < 0 – линию.

То есть каустика получает вторую ветвь, содержащую фокальную линию, прости-

рающуюся с вершины клюва к поверхности воды рис. 6.15. На этой линии не определе- но множество пересечений лучей. Напри- мер, внутри клюва в двухмерном случае пе- ресекалось три луча. Вне клюва – два. Эта неопределённость связана с неопределён-

ностью азимутальной координаты β на этой линии. Поэтому на линии пересекается не- определённо много лучей с любой величиной β. Отсюда точка фокуса в трёхмерном случае оказывается более неустойчивой, чем в 2 двухмерном случае.

соотношения:

)

При наличии на поверхности раздела поверхностного заряда с нормальная компонента вектора электри-

)

ческой индукции испытывает скачёк равный 4рс .

Найдём граничные условия для тангенциальных компонент.

)r

Заменим поверхность раздела переходным слоем прямоугольной площади, где b – единичный вектор к плоскости прямоугольника P1Q1P2Q2. Рассмотрим одно из уравнений Максвелла:

где точка над буквой означает дифференцирование по времени. Пусть P1Q1 = dS1, а P2Q2 = dS2 очень малы. Тогда на этих длинах E1 и E2 не меняются. Пусть ∂h стремится к нулю, тогда S → 0, и:

тангенциальная компонента напряжённости электрического поля непрерывна на границе раздела диэлек- триков.

Аналогично доказывается, что:

Нормальная компонента магнитного поля при отсутствии токов на границе раздела непрерывна.

Пусть волновой вектор падающей волны лежит в плоскости см. рис. 8.1, тогда kiy = 0 . Это

условие выполняется, если пренебречь потоком через боковые поверхности (оптический эффект Маг- нуса), тогда:

Постулируется, что луч падающий, отражённый и преломлённый лежат в одной плоскости с нормалью в плоскости падения (рис. 8.1, б). Это условие выполняется только приблизительно на пло- ских границах раздела двух сред и вообще не выполняется на кривых границах!

Разложим волновой вектор на составляющие:

где v1 и v2 – скорости волны в средах с абсолютным показателем преломления n1 и n2. Тогда из (8.5) и (8.7) следует:

Выражение (8.9) характеризует два закона Снеллиуса: закон отражения (угол падения равен углу от- ражения)

ϕ = ϕ′, (8.10)

и закон преломления:

Соотношения между амплитудами падающей, отражённой и прошедшей волн. Формулы Френеля.

Отобразим компоненты электрического вектора для падающей, отраженной и преломленной волн на рис. 8.2. Разложим вектор напряжённости поля на две компоненты: параллельную и перпендикуляр-

В соответствии с (8.13) и (8.14 а) получим систему уравнений:

Согласно уравнению: μ H = ε ( k × E) с учетом того, что для прозрачной среды μ = 1, представим вектор магнитного поля через компоненты электрического поля:

Для падающей волны вектор магнитного поля можно представить в виде:

Разложим вектор Нi по компонентам поля:

Hxi = −ε1Eyi cosφ, Hiy = ε1 (Exi cosφ − Ezi sinφ), Hiz = ε1Eiy sinφ .(8.19 а)

Соответственно, для отраженной волны вектор магнитного поля:

Разложим по компонентам магнитного поля:

Hxr =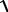ε1Eyr cosφ, Hry =ε1(−Exr cosφ −Ezr sinφ), Hrz =ε1Eyr sinφ. (8.19 б)

И для преломленной волны:

Подставим компоненты поля (8.19) в уравнения (8.14 б) для компонент x поля, получим:

− ε1 Eyi cosφ + ε1 Eyr cosφ = −ε2 Eyt cosψ .

Исходя из (8.13), приведем вышестоящее выражение к виду:

Аналогично поступим для y компонент поля:

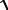
ε1 (Exi cosφ − Ezi sinφ) + ε1 (−Exr cosφ − Ezr sinφ) = 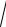ε2 (Ext cosψ − Ezt sinψ ) .

Преобразуем это выражение, используя (8.13):

ε1 (Eip cos2 φ + Eip sin2 φ) + ε1 (Epr cos2 φ + Epr sin2 φ) = ε2 (Etp cos2ψ + Etp sin2ψ )

Упростим вышестоящее выражение:

Подставим значение ESt в уравнение (8.20 а), получим: