Lections_V

r

Для действительных E и H в плоской волне вектор Пойтинга примет вид:

c

)

r

S =

EH × s

. Воспользуемся уравнением (2.15), тогда:

4π

c 2π

c

c

r

c

r

r r

r r

2

2

E × H =

E × k × E =

[k E

− E (kE )]=

k E

=

Es

=

Es ,

ωμ

ωμ

ωμ

ωμ λ

r

c

2

r

ε E

откуда для μ = 1 следует: S

=

× s

(3.19)

4

π

1

T

c

E 2 =

c

E 02 ,

ε

ε

I = S

=

(3.20)

T

ò0 4π

8π

где Т – период световых колебаний,

- величина потока энергии излучаемого усреднен-

S

ного по времени. Если v =

c

, то (3.20) можно представить в виде: I =

v × w

, (3.21)

4 π

ε

где

w =

E 02

ε

- объемная плотность энергии.

r

2

Или

w × v

,

(3.22)

r

r

S =

4π

где v

= v × s .

r

1 c

r r *

S

=

Re(E ´ H

) . Уравнение (3.12) представим как:

2 4π

r

æ

1

öæ

c ö

r r

r

r

S

= ç

֍

÷{E ´ H + E ´ H}

(3.23)

4

è

øè

4π ø

Вопрос № 56

Вариационный интеграл . Принцип Ферма. Примеры применения

Пьер Ферма (1601-1675) выдвинул принцип,

ds

согласно которому свет при распространении из

одной точки в другую выбирает путь, которому

S

соответствует наименьшее время распространения

n(x,y,z)

dl=n(x,y,z)dS

А

В

l =

òn(x, y, z)dS – интеграл действия.

Рис. 5.1 Распространение луча

AB

δ òn(x, y, z)dS = 0

(5.1)

в неоднородной среде.

AB

Принцип Ферма не доказывается, а постулируется!

Вопрос № 57

Идеальные оптические инструменты.

Задача 1. Найти форму поверхности, разде-

ляющей две среды с показателями прелом-

Y

B

ления n и n`, которая собирает параллельный

пучок лучей в одну точку. Это задача о без-

абберационных линзах. Сферическая линза

n

n `

X

не может собрать все лучи в одну точку.

B`

Будем исходить из принципа Ферма. Лучи,

P`

распространяющиеся по пути AB − BP′

и по

пути OP′ , собираются в одной точке P′ . Сле-

довательно, они затрачивают на прохожде-

Рис. 5.2

Прелом ление лу чей на

ние разных геометрических путей одинако-

сф ер ической поверхно сти.

вое время. Поскольку обе среды однородны,

то оптический путь вдоль обеих траекторий будет одинаков:

n

×

AB

+

n

′×

BP

=

′

′

.

n OP

Точка В имеет координаты (x, y) а точка P ′

– точка фокуса (x = f, y = 0).

′

2

′

2

′

′

2

или BP

′

=

( f − x)

2

+ y

2

,

AB = x , следовательно:

(BP )

= (BB )

+ (B P )

nx + n′

( f − x)2 + y2

= n′ f

(5.2)

Уравнение (5.2) и есть уравнение искомой поверхности:

′2

− n

2

)x

2

′2

y

2

′

′

− n) fx = 0

(5.3)

(n

+ n

− 2n (n

Будем считать, что n′2

− n2

> 0 , тогда:

′2

− n

2

)x

2

′

′

− n) fx = (n

¢ -

ì

¢ +

n)x

2 -

¢

+ n¢2 f 2

-

n¢2 f 2 ü

=

(n

− 2n (n

n)í(n

2n fx

(n¢ + n)

(n¢

ý

î

+ n)þ

ì

é

n¢f

ù

2

n¢

2

f

2 ü

é

n¢f

ù

2

2 n¢ - n

¢

¢

¢

¢2

= (n

ï

-

ï

;

-

2

f

- n)í

êx -

(n¢ + n)

ú

ý

(n - n)êx

ú

+ n y

= n

n¢ + n

ïë

û

(n¢ + n) ï

ë

(n¢ + n)û

î

þ

(x − x )2

+

y2

=1

b

2

= f

2 n′ + n

a

2

=

n′2 f 2

a

2

0

b

2

(5.4)

n¢ - n

n′ + n

n(r) =

n0

1+

r2

(5.8)

a2

(ds)

2

= (dx)2

+ (dz)2

(5.9)

n1 sin φ1

и законом Снелля:

n1 sinφ1 = n sin φ , запишем:

sin φ =

dz

,

но sin φ =

dz

n1 sin φ1

n

ds

n

Следовательно:

=

или ds =

dz .

(5.10)

ds

n

n1 sin φ1

Тогда из (5.9) с учетом (5.10) находим:

æ dx

ö

2

n2

dx d 2 x

1

dn2

ç

÷

=

-1 или 2

2

=

.

n

2

sin

2

φ

dz dz

n

2

sin

2

φ dz

è dz

ø

1

1

1

1

Или окончательно получаем уравнение эйконала:

d 2 x

=

1

dn2

(5.11)

dz2

2n2 sin2

φ

dx

1

1

n

2

2

~

2

.

(x) = n0 − nx

Тогда из уравнения (5.11) находим:

d 2 x

1

=

x(z)

(5.12)

dz2

n2 sin2

φ

0

0

Частное решение (5.12) имеет вид:

æ

~

ö

h1/ 2 z

ç

÷

(5.13)

x(z) = Asinç n sinφ

0

+ Φ0 ÷

è

0

ø

Период траектории при Φ0 = 0, ϕ0 = π/2:

~1 / 2

2π

h

zт = 2π

или

zт =

(5.14)

n0

n0

~

h

Если полный радиус внешней окружности: R = 1+1/ 2 = 3/ 2, то кончик острия распола-

гается на половине радиуса внешней окружности R=1/2. Причем внешнюю окруж-

ность мы можем отождествить с вогнутым цилиндрическим зеркалом радиуса R. На

это зеркало падает параллельный пучок лучей. Если строго подойти к построению

этих лучей, то они никогда не соберутся в одной точке – фокусе. Такая возможность

при строгом построении предоставляется только очень малой части приосевых лучей

(параксиальных лучей), которые составляют после отражения очень малые углы с оп-

тической осью. Если точка О – оптический центр зеркала, то параксиальные лучи со-

берутся в точке, расположенной на половине радиуса R/2.

Тем не менее, для широкой апертуры зеркала, когда захвачены все лучи, наибо-

лее яркой точкой является точка возврата каустики. Именно в этой точке располагает-

ся геометрический фокус вогнутого зеркала. Если теперь постараться представить всю

каустическую поверхность, то необхо-

димо просто транслировать плоскость xy

Z

вдоль прямых образующих цилиндриче-

ские стенки стакана (рис. 6.5).

Y

На эксперименте (рис. 6.2) мы на-

блюдаем только ту часть каустики, кото-

X

рая рассеивается на шероховатой по-

верхности экрана, на котором стоит ста-

кан. Очевидно, для того чтобы наблю-

дать эту каустику необходимо спроеци-

ровать её с помощью оптической систе-

Рис. 6.5. Проекция каустической

мы на второй экран. Без первого рассеи-

поверхности на плоскость X Y.

вающего экрана увидеть каустику не-

возможно. Каустика – эволюта волнового фронта. Волновой фронт – эвольвента кау-

стики.

В общем случае от цилиндрической поверхности отражается пространственный (а не

плоский) пучок лучей. Эти лучи

z

падают под углом к плоскости

нормалей к цилиндру. Это су-

щественно изменяет ситуацию.

В самом деле, в отличие от рис.

α

6.3 теперь имеется два управ-

ляющих параметра: угол υ -

азимутальный угол и угол α -

полярный угол, который со-

а)

б)

ставляют лучи, падающие на

цилиндрическую поверхность с

Рис. 6.6.

а) Возни кновение второго управляю щего

плоскостью нормалей. Все лучи

параметра α. б) Образование точек возврата

при α = const лежат в одной

(ка тастрофа) на волновом фронте.

плоскости, которая сечет ци-

линдр под углом к оси. Эта плоскость – эллипс (рис. 6.6 а). На самом деле, мы имеем

дело с отражениями не от круглого зеркала, а от эллиптического. Рассмотрим самый

простой случай: Пусть каждая точка эллипса излучает свет (рис. 6.6 б). Восстановим

нормали к эллипсу. Линия, перпендикулярная к нормалям образует два листа волново-

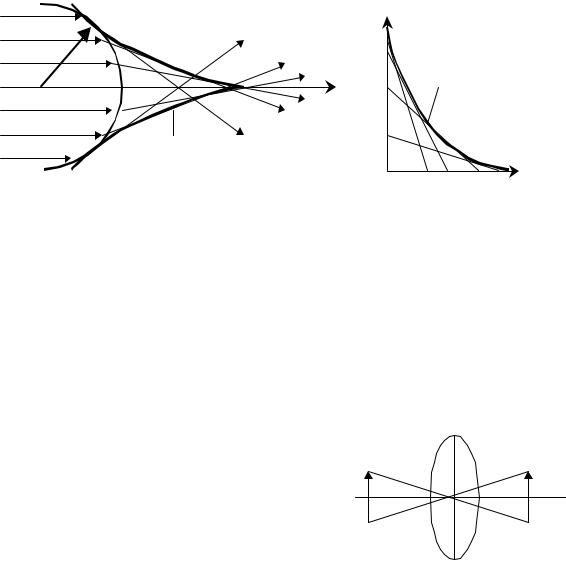
го фронта. Это значит, что единой волновой поверхности уже нет. На волновом фронте

образуются точки возврата, что приводит к катастрофе. Оказывается, что поверхность

каустики уже нельзя восстановить простой параллельной трансляцией нефроиды. Не-

обходимо учитывать еще один управляющий параметр α.

Второй тип каустик, возникает при прохождении лучей через стакан.

Каустика, возникающая после цилиндрической линзы – циклоида, уравнение которой

имеет вид:

υ

ì

3

ï x = l cos

, где l – оптический путь лучей. Этот путь одинаков для всех лучей. После

í

3

υ

ï

î y = l sin

линзы эти лучи сходятся не в одной точке (рис. 6.7), а огибающая лучей образует цик-

Y

R

Z

циклоида

циклоида

X

а

б

Рис. 6.7.Каустика, возникающая после цилиндрическойлинзы (а). Геометрическое построение циклоиды

какогибающейсемейства отрезков, опирающихся на взаимно перпендикулярные прямые (б).

лоиду.

Заметим важную особенность построения лучей (рис. 6.3):

1) Внутри клюва пересекаются три отражённых луча.

2) За каустикой пересекаются только два луча.

Это связано с тем что, при отражении луча от каустики меняется его фаза. В нашем

случае вблизи клюва каустики фаза изменяется на π - аномальная фаза Гуи при прохо-

ждении света через фокус (рис. 6.8).

δ → δ−π

В случае простых каустик, например, ра-