5_Zakony zberezhennia

204

імпульсу системи P , який є сумою векторів імпульсів частинок, до їх зіткнення P p1 p2 ,

P . Так само в одній площині з

і ці імпульси p1 та

p2 лежать в одній площині з вектором

вектором P лежать

вектори

p1

та

p2 . Ці площини

відповідно

до рівняння

(5.152)

перетинаються по лінії P p1

p2 .

Надалі ми будемо зображати лише діаграму імпульсів

ABC , всі вектори якої лежать в одній площині.

Обмежимось випадком абсолютно пружних зіткнень. При цьому точка C так само як і

точка D , не може бути віддалена як завгодно далеко від точок A і B ,

оскільки максимальна

p2

p2

p 2

p 2

E

1

2

1

2

E .

2m1

2m2

2m1

2m2

~

~

,

~

~

,

(5.170)

V

,

2

V

2

V

,

V

1

C

1

C

1

C

1

2

C

2

яке відповідає

аналогічному

співвідношенню для

радіус-векторів частинок (див.

Рис. 5.11)

~

~

~

~

r1

RC

r1

, r2

RC

r2

, r1 RC

r1 ,

r2

RC

r2 ,

(5.171)

~

m

~

m

r

2

r

і r

2

r , де M m

m

, r

r

r .

1

M

2

M

1

2

1

2

~

m

~

m

Аналогічно, r

2

r

і r

1

r

.

1

M

2

M

~

m

~

m

~

m

~

m

2

,

2

,

2

,

2

,

(5.172)

2

1

M

M

1

M

2

M

частинок відносно лабораторної системи відліку, p1

p2 (вектор AB ).

Знайдемо точку

O ,

яка

ділить

цей

вектор

у

відношенні

m1 m2 .

Нехай

C

m

m

AO

1

( p1 p2 ) ,

а

OB

2

( p1

p2 ) .

M

M

p

p

1

2

n0

Тоді

геометричне

місце

кінців

можливих

n0

A

O

1

векторів

p , що мають початок в точці O ,

є

B

коло описане кінцем вектора n0 , початок

якого

лежить

в

точці

O . На Рис. 5.30

показано одне з можливих положень вектора

,

кінець

якого

лежить в точці

C на

n0

Рис. 5.30. Діаграма імпульсів

згаданому

колі.

Тоді

вектор

p

p

2

AC

1

n

p

репрезентує імпульс частинки

m

в лабораторній системі відліку

M

0

1

1

p1

p2

після зіткнення. Аналогічно вектор CB

n

0

p

репрезентує імпульс частинки

M

2

m2 в лабораторній системі відліку після зіткнення. З викладеного вище зрозуміло,

що радіус

та початки векторів

залежить від повної механічної

кола, на якому лежать кінці векторів p

p

1

2

енергії системи частинок,

~

Ця величина і є кількісною мірою обмеження, яке

2 E .

накладає закон збереження енергії на величини імпульсів частинок після зіткнення.

Ясно, що

при заданих m1 , m2 , 1

, 2

радіус кола і його положення відносно точок A і B залишаються

сталими,

а точка

C може займати будь-яке положення

на

цьому у колі. Цим,

власне, і

повний імпульс системи дорівнює імпульсу першої частинки,

p1

. Тоді вектор

m

m

OB

2 1

, оскільки у цьому випадку вектор відносної швидкості до зіткнення

M

1

1

співпадає з вектором швидкості першої частинки

1 . Це означає, що

OB

OC

і, таким

чином, точка B також лежить на колі з радіусом

і центром в точці O (Рис. 5.31а).

Частинка

tg 1

sin

.

(5.181)

cos

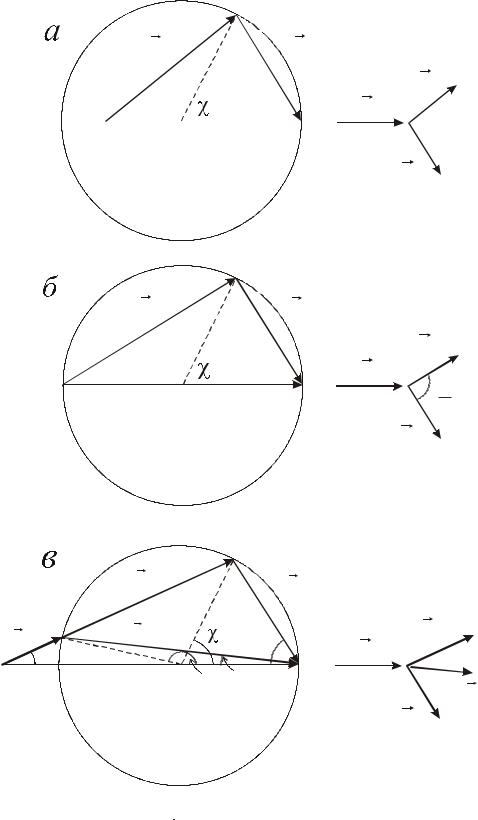
З діаграми розсіяння для частинок однакової маси

m2 m1 (Рис. 5.31б) безпосередньо

210

розсіяння 1 першої частинки в загальному випадку можуть відповідати два різних кута

розсіяння в СЦМ,

та відповідно різного положення точок C та C . Цим двом кутам

та відповідають

два різних кути розсіяння другої частинки

2

та в лабораторній системі

2

відліку, і, відповідно, два різні вектори імпульсу

p та

p . Максимальний кут розсіяння

2

2

1

частинки m1 досягається, коли відрізок AC направлений по дотичній до кола (точки C та C

збігаються). При цьому трикутник ACO стає прямокутним, оскільки сторона OC є радіусом

для максимального кута розсіяння 1 легко

кола перпендикулярним до дотичної AC . Тоді

дістати

sin

OC

m2

.

(5.182)

max

m1

AO

m

m1

M

1

E

( p )2

2

.

(5.183)

2

2m2

На підставі (5.181)

одержимо

( p )

2

m2

m2

p n

p n

2

1

0

1

0

M

M

m22

2

2

m2

p1

2

p1n0

M 2

M

m22

2

2 2

m2

p1

2

p1 cos( p1

n0 )

(5.184)

M 2

M

m2

m2 2

m2m2

2

2

m m m

2

m 2

cos

2

1

2

1

2

M 2

M 2

1

M

M

1

m2m2

2

(1 cos ) 4

m2m2

2 sin2

2

1

2

1

2

.

M 2

M 2

2

Отже

E 2

m2m

2 sin2

1

2

.

(5.185)

M 2

2

2

E

m 2

.