
5_Zakony zberezhennia
.pdfРозділ 5
ЗАКОНИ ЗБЕРЕЖЕННЯ
Три закони динаміки частинки – три закони Ньютона, розглянуті в попередньому розділі
дають можливість розв’язувати значну кількість практично важливих задач.
Однак для їх успішного застосування необхідно знати сили, прикладені до частинки в кожний момент часу, що не завжди можливо. На точність результату знаходження як швидкості частинки, так і її радіус-вектора також суттєво впливає точність, з якою відомі
початкові умови.
Ситуація принципово ускладнюється, якщо йдеться про опис механічного руху значної кількості частинок, які утворюють систему частинок, що взаємодіють між собою. Механічний стан системи частинок ми будемо вважати заданим, якщо відомі положення і швидкості всіх
частинок системи в деякий момент часу. |
Іншими словами механічний стан системи, що |
|||
складається |
з n частинок визначається у |
будь-який момент часу t |
сукупністю величин |
|
|
|
|
|
|
ri |
(t), i (t) , |
де індекс і змінюється від 1 до n. Якщо механічний стан системи відомий в деякий |
||
|
|
|
|
|
початковий момент часу (при t 0 ), тобто відомі початкові умови ri (0), i (0) , то величини |
||||
|
|
|
|
|
ri |
(t), i (t) можуть бути, в принципі, знайдені з n рівнянь руху, записаних |
для кожної частинки |
||
окремо:
|
|
|
|
|
|
|
|||
mai |
Fi , i 1, n . |
(5.1) |
||
Таким чином, у загальному випадку необхідно розв’язувати |
3n скалярних рівнянь при |
|||
6n початкових умовах.
У цьому випадку:
а) сила, що діє на кожну частинку системи в кожний момент часу, як правило, не відома;
б) неточність у початкових умовах окремої частинки може радикально змінити рух цієї частинки, а через це й інших частинок;
в) при дуже великій кількості частинок (наприклад, молекул газу в деякому макроскопічному об’ємі) розв’язання величезної кількості рівнянь стає нездоланою перешкодою навіть для сучасних комп’ютерів.
135
І, нарешті, останнє, можливо найбільш суттєве: якби навіть вдалося обчислити радіус-
вектори (координати) всіх частинок системи та їх швидкості в будь-який момент часу, то це була б сукупність характеристик поведінки окремих частинок, а не системи в цілому.
Розглянемо простий приклад. Нехай ми маємо дві системи частинок – молекул деякого газу,
взятого в кількості одного моля в двох різних посудинах, що мають, наприклад, різні об’єм або форму.
Якщо навіть уявити, що нам вдалося розрахувати траєкторії і швидкості всіх молекул (а їх кількість у
кожній посудині дорівнює числу Авогадро |
N |
A |
6,022 1023 |
), то зробити якесь порівняння |
механічного стану цих двох систем частинок на підставі цих колосальних масивів даних практично неможливо. Також цілком очевидно, що додавання однієї, десяти, чи навіть тисячі молекул до будь-якої з вищезгаданих систем частинок не спричинить суттєвої зміни її макроскопічної поведінки.
Отже, постає задача знайти такі величини, які б характеризували механічний стан системи в цілому через характеристики механічного стану її частинок і при цьому не залежали б у явному вигляді від механічного стану кожної окремої частинки.
Наш план буде такий.
Спочатку ми знайдемо величини, які є функціями механічного стану частинки, але залишаються незмінними (сталими) в процесі вільного руху частинки, тобто такого, коли відсутня її взаємодія з іншими матеріальними об’єктами. Про такі величини кажуть, що вони зберігаються.
На другому етапі ми з’ясуємо, внаслідок чого можуть змінюватися величини, які були незмінними для вільних частинок, і за яких умов ці величини можуть залишатися незмінними і для частинок, які вже не є вільними, а взаємодіють з іншими матеріальними об’єктами.
На третьому етапі ми розглянемо систему частинок, які не взаємодіють а ні між собою а ні з іншими матеріальними об’єктами. Таку систему можна розглядати як сукупність вільних частинок. Побудуємо суми знайдених на першому етапі величин, які залишаються незмінними
(сталими) в процесі вільного руху однієї частинки, для всіх частинок системи. Очевидно, що такі суми також будуть залишатися незмінними (сталими) в процесі руху вільних частинок частинок цієї сукупності. При цьому кожна з цих сум буде функцією величин, які характеризують механічний стан частинок системи, а саме їх радіус-векторів і векторів швидкості.
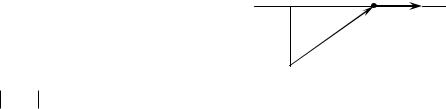
136
На четвертому етапі ми проаналізуємо умови зміни та збереження сум згаданих вище величин, побудованих на третьому етапі, які були незмінними для вільних частинок, а також з’ясуємо за яких умов ці суми можуть залишатися незмінними і для частинок, які вже не є вільними, тобто взаємодіють з іншими матеріальними об’єктами.
5.1. Імпульс, момент імпульсу, кінетична енергія частики
Розглянемо спочатку рух вільної частинки з масою m . Її механічний стан визначається її
|
|
|
радіус-вектором r |
r (t) |
та швидкістю const . Можна вказати деякі величини, які є |
функціями змінних, що визначають механічний стан частинки, але залишаються незмінними або, як прийнято говорити, зберігаються в процесі її руху. Легко бачити, що такими
|
|
2 |
|
2 |
, |
|
3 |
2 |
|
4 |
( |
2 |
) |
2 |
, ... |
величинами є сама швидкість |
та її степені ( ) |
|
|
|
( ) |
|
, |
( ) |
|
|
|
|
|
|
|
Ясно, що всі степені вище другого можуть бути подані через добутки вектора та скаляра |
|||
|
|
|
|
2 , тому ми надалі розглядатимемо лише вектор та скаляр 2 . Радіус-вектор r вільної |
|||
|
|
|
|
частинки на відміну від швидкості сам по собі не залишається незмінним r , але легко бачити, |
|||
що залишається незмінною його проекція rp |
на перпендикуляр, |
опущений з початку O на |
|
|
|
|
|
прямолінійну траєкторію частинки (Рис. 5.1), |
rp r sin(r |
) . |
Цілком зрозуміло, що буде |
зберігатися і добуток проекції rp на модуль швидкості ,
тобто величина r sin(r ) . Але ця величина є не що
інше як модуль векторного добутку векторів r та ,
тобто r sin(r ) [r ] . Звідси випливає, що
m
rp |
|
r |
O
Рис. 5.1. Рух вільної частинки.
векторний добуток |
|
оскільки |
|
[r ] const, |
при вільному русі частинки вектор r завжди |
||
лежить у площині, |
яка проходить через початок відліку O та пряму, вздовж якої рухається |
||
частинка. Таким чином, існує три |
суттєво |
різні величини, які залишаються сталими при |
|
|
|
|
|
вільному русі будь-якої частинки: , 2 та |
[r ] . Але, як ми бачили, динамічні властивості |
||
частинки визначаються величиною її маси m , яка також є сталою величиною, але може бути різною для різних частинок. Тому при вільному русі частинки також будуть зберігатися добутки знайдених вище трьох величин на масу m , а також на будь-які сталі числові
137
коефіцієнти. Із врахуванням сказаного можна побудувати три величини, які залишаються незмінними при русі вільної частинки, а саме:
|
|
|
|
|
|
|
|
|
|||
векторну величину p m |
, яку називають імпульсом частинки; |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||
векторну величину L |
[r p] m[r ] , яку називають моментом імпульсу частинки, і |
||||||||||
скалярну величина T |
m 2 |
, яка зветься кінетичною енергією частинки. |
|||||||||
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||
Таким чином, імпульс, момент імпульсу та кінетична енергія вільної частинки |
|||||||||||
завжди зберігаються. |
|
|
|
|
|
|
|
|
|
||
У той час, |
коли напрям |
|
|
вектора |
імпульсу |
|
|
|
|||
|
|
частинки p |
|||||||||
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
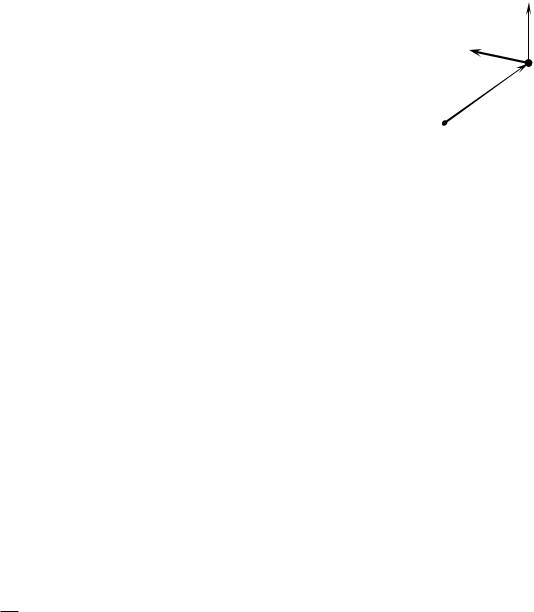
співпадає з напрямом її швидкості , напрям моменту імпульсу L є |
|||||||||||
перпендикулярний як до вектора швидкості частинки, |
так і до її |
m |
|||||||||
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
радіус-вектора, причому вектори |
|
|
|
утворюють |
r |
||||||
r , p (або ) та |
L |
O |
|||||||||
|
|
|
|
|
|
|
|
|
|
||
праву трійку векторів (Рис. 5.2). |
|
|
|
|
|
|
Рис. 5.2. Вектор моменту |
||||
|
|
|
|
|
|
|
|
|
|
||
Розмірності |
введених |
|
|
нами |
величин |
|
випливають |
|
|||
безпосередньо з їх формул: розмірність імпульсу є кг м с 1 , моменту імпульсу кг м2 с 1 ,
кінетичної енергії кг м2 с 2 .
З’ясуємо за яких умов і за рахунок чого можуть змінюватися з часом імпульс, момент імпульсу та кінетична енергія частинки, що не є вільною. Для цього обчислимо похідні за
часом від цих величин.
Умови зміни та збереження імпульсу частинки. Для знаходження умов зміни з часом
деякої величини та умов її збереження необхідно дослідити похідну за часом від цієї величини.
Похідна від імпульсу за часом є
|
|
|
|
|
|
|
dp |
m |
d |
, |
(5.2) |
|
dt |
dt |
|||
|
|
|
|
||
або, з врахуванням другого закону Ньютона, |
|
||||
|
|
|
, |
|
(5.3) |
|
dp F |
|
|||
|
|
|
|
|
|
dt

138
де F – сума сил, що прикладені до частинки. Отже, імпульс частинки змінюється під
дією прикладеної до неї сили, причому елементарний приріст імпульсу dp співпадає з
напрямом цієї сили, а його величина пропорційна величині сили та проміжку часу, протягом якого цей приріст імпульсу виникає:
|
|
(5.4) |
dp Fdt . |
||
|
|
|
|
|
Рівняння (5.4) дає можливість за відомою залежністю сили F від часу обчислювати зміну |
||||
|
|
|
|
|
імпульсу p за певний проміжок часу |
|
|||
|
t2 |
|
t2 |
|
p |
dp F (t)dt . |
(5.5) |
||
|
t1 |
|
t1 |
|
Із рівняння |
(5.3) випливає умова збереження імпульсу частинки: |
імпульс частинки |
||
зберігається, якщо сума всіх сил, що прикладені до частинки, дорівнює нулю.
Зауважимо, що імпульс вільної частинки зберігається безумовно (без будь-яких умов),
оскільки за означенням на вільну частинку не діють ніякі сили.
Умови зміни та збереження моменту імпульсу частинки. Похідна від імпульсу за
часом є |
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
dL |
|
dr |
dp |
|
|
||||
|
|
|
|
([r p]) [ |
|
p] [r |
|
] , |
(5.6) |
|
|
dt |
dt |
dt |
dt |
||||||
або, із врахуванням другого закону Ньютона у формі (5.3) та того, що векторний добуток
|
|
|
|
dr |
|
[ |
|
p] 0 внаслідок колінеарності співмножників, одержимо |
dt |
|
|
|
|
|
|
dL |
|
||
|
|
[r F ] . |
(5. 7) |
|
|
dt |
|||
Величину |
|
|||
|
|
|
|
(5.8) |
|
M |
[r F ] |
||
називають моментом сили F . Таким чином, момент імпульсу частинки змінюється під дією
моменту прикладеної до неї сили,
dL M , |
(5.9) |
dt
139
причому елементарний приріст вектора моменту імпульсу частинки dL співпадає за напрямом з напрямом вектора моменту сили, а його величина пропорційна величині моменту цієї сили та проміжку часу, протягом якого цей приріст моменту імпульсу виникає:
|
|
|
|
|
|
|
|
dL |
Mdt . |
|
|
|
(5.10) |
||
Рівняння (5.9) іноді називають рівнянням моментів. |
Зауважимо, що коли до частинки |
||||||
|
|
|
|
|
|
|
|
одночасно |
прикладемо декілька сил, то під |
M у |
правій |
частині рівняння моментів (5.9) |
|||
необхідно розуміти суму моментів всіх сил, |
що прикладені до частинки. Рівняння (5.9) дає |
||||||
|
|
|
|
|
|
|
|
можливість за відомою залежністю моменту сили |
M від часу обчислювати зміну моменту |
||||||
|
|
|
|
|
|
|
|
імпульсу L за певний проміжок часу |
|
|
|
||||
|
|
t2 |
|
t2 |
|
|
|
L |
dL |
M (t)dt . |
|
|
(5.11) |
||
|
|
t1 |
|
t1 |
|
|
|
З рівняння моментів (5.9) випливає умова збереження моменту імпульсу частинки:
момент імпульсу частинки зберігається, якщо сумарний момент усіх сил, прикладених до
частинки, дорівнює нулю.
Зауважимо, що момент імпульсу вільної частинки зберігається безумовно, оскільки за означенням на вільну частинку не діють ніякі сили, отже, сумарний момент сил завжди дорівнює нулю.
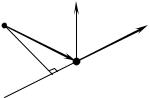
Вектор моменту сили F за означенням направлений перпендикулярно до цієї сили та до
|
|
|
радіус-вектора частинки. Його модуль M rF sin(r |
F ) . Іноді модуль вектора моменту сили |
|
|
|
|
записують у вигляді M Fl , де введено величину l r sin(r |
F ) , яку називають плечем сили |
|
F відносно точки O . Як видно з Рис. 5.3, |
плече сили l є |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
M |
|
найкоротша |
відстань |
від |
точки |
O , |
відносно |
якої |
O |
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
r |
F |
|
|
|
|
|
|
|
|
l |
||||
визначається |
момент |
сили |
F , |
до |
лінії дії сили |
F . |
m |
||||
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Зрозуміло, що коли |
лінія |
дії |
сили |
F проходить через |
|
|
|||||
|
|
|
|
|
|
|
|
0 , |
Рис. 5.3. Вектор моменту сили. |
||
|
|
|
|
|
|
||||||
точку O ( це означає, між іншим, що F |
|
r ), то M |
|
|
|||||||
незалежно від величини модуля сили F .

140
Умови зміни та збереження кінетичної енергії частинки. Похідна від кінетичної
енергії за часом є
|
dT |
|
d m 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
d m( ) |
|
m d ( ) |
|
m d |
d |
|
d |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
dt |
|
|
|
2 |
|
|
dt |
2 |
|
2 dt |
|
2 dt |
|
|
dt |
|
|
dt |
|
|||||||
|
|
dt |
|
|
|
|
|
|
|
|
|||||||||||||||||
або з урахуванням другого закону Ньютона |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
dT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
F . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рівняння (5.13) можна записати у вигляді
dTdt N ,
де введено скалярну величину
N F ,
(5.12)
(5.13)
(5.13а)
(5.14)
яку називають потужністю сили F . Таким чином, кінетична енергія частинки
змінюється, якщо сумарна потужність прикладених до неї сил відмінна від нуля.
З рівняння (5.13) випливає умова збереження кінетичної енергії частинки: кінетична
енергія частинки зберігається, якщо сумарна потужність усіх прикладених до частинки
сил дорівнює нулю.
Кінетична енергія вільної частинки зберігається безумовно, оскільки за означенням на вільну частинку не діють ніякі сили, а, отже, потужність у правій частині рівняння (5.13)
завжди дорівнює нулю. Тому говорять не про умову, а про закон збереження кінетичної енергії
вільної частинки: кінетична енергія вільної частинки зберігається.
Елементарний приріст кінетичної енергії dT частинки за проміжок часу dt є
dT Ndt . |
(5.15) |
Величину |
|
A Ndt |
(5.16) |
називають елементарною роботою. |
Ясно, що розмірність роботи збігається з розмірністю |
енергії. У системі СІ одиницею роботи є джоуль ( Дж ), 1 Дж кг м2 с 2 , а одиницею
потужності є ват ( Вт ), 1 Вт Дж с 1 .
|
|
141 |
|
|
|
Оскільки Ndt F dt |
Fdr , то можна записати |
|
|
|
(5.17) |
A Fdr . |
|
|
|
|
|
Елементарну роботу у вигляді (5.17) називають елементарною роботою сили F на |
||
|
|
елементарному переміщенні dr . |
|
Рівняння (5.15) можна переписати так |
|
dT A . |
(5.18) |
Отже, кінетична енергія частинки змінюється за рахунок сумарної роботи сил,
прикладених до частинки.
5.2. Робота та потенціальна енергія
Як видно з (5.17), елементарна робота є величина алгебраїчна, тобто вона може бути як
|
|
|
|
|
|
|
|
|
|
(або, що |
додатною, так і від’ємною, залежно від кута між напрямом вектора переміщення dr |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
теж саме, вектора швидкості ) та напрямом сили |
F і її можна подати як скалярний добуток |
|||||||||
сили на елементарне переміщення, записаний в декількох еквівалентних формах : |
|
|||||||||
|
|
|
|
dr Fdr , |
|
(5.19) |
||||
A Fdr |
Fdr cos(F |
dr ) F |
|
|||||||
|
|
|
|
|
|
|
dr |
F |
|
|
де F |
|
|
|
, |
|
|
|
– проекція |
|
|
|
|
|
||||||||
|
F |
|
F F cos(F |
dr ) |
сили F на напрям переміщення dr , |
|||||
|
|
|
|
|
dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
dr dr cos(F dr ) – проекція переміщення dr на напрям сили F . |
|
|||||||||
F |
|
|
|
|
|
|
||||
Робота A12 сили F на деякій ділянці траєкторії частинки при її переміщенні від точки 1 до
точки 2 є сума елементарних робіт при елементарних переміщеннях вздовж траєкторії, яка виражається визначеним інтегралом
2 |
|
2 |
2 |
|
|
A12 Fdr |
Fdr dr Fdr (s)ds , |
(5.20) |
|||
1 |
|
1 |
1 |
|
|
де |
Fdr (s) – |
проекція |
сили |
на |
|
переміщення |
в |
точці |
траєкторії |
s , а |
ds – |
елементарний шлях вздовж траєкторії. Такому інтегруванню може бути надано геометричну
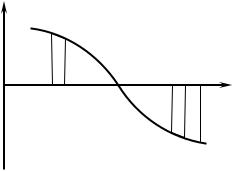
Fdr |
|
|
A 0 |
|
|
0 |
|
|
s2 |
||
|
|
||||
|
|
|
|||
s1 |
s s+ds |
s |
|||
|
|||||
A 0
Рис. 5.4. До обчислення роботи сили.
інтерпретацію подану на Рис. 5.4, де наведено графік Fdr (s) . Елементарна робота дорівнює

142
площі між кривою та віссю абсцис на ділянці від s до s ds взятій зі знаком «+», якщо крива
проходить у верхній напівплощині, і зі знаком «–», якщо крива проходить у нижній напівплощині.
З попереднього цілком зрозуміло, що у випадку, коли до частинки прикладемо декілька
|
|
|
|
|
n |
|
|
|
|
|
|
|
сил F1, F2 , F3 , ...Fn , |
результуюча яких є F |
Fi , |
i 1, n , то робота цієї результуючої сили |
|||||||||
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на деякому переміщенні дорівнює сумі робіт, здійснюваних кожною із сил F1 , F2 , F3 , ...Fn :
2 |
2 |
|
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
|
|
|
A Fdr |
(F1 |
F2 |
|
... Fn )dr |
F1dr |
F2dr |
... Fndr |
A1 A2 ... An |
|||||||||
1 |
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
або A Ai , |
i 1, n . |
|
|
|
|
|
|
|
|
|
|
|
(5.21) |
||||
i
Зрозуміло, що потужність, так само як і робота, може бути додатною, від’ємною або рівною нулю, і при наявності декількох сил обчислюється як сума потужностей:
n
N Ni , i 1, n .
i
Рівняння (5.15) дає можливість за відомою залежністю потужності від часу обчислювати зміну кінетичної енергії за певний проміжок часу
t2 |
t2 |
|
T dT N (t)dt . |
(5.22) |
|
t1 |
t1 |
|
Розглянемо приклади обчислення роботи.
Приклад 1. Обчислити мінімальну роботу по перетягуванню по горизонтальній підлозі блока живлення лазера з одного кутка лабораторного приміщення, що має форму квадрата зі стороною 10 м, у
протилежний куток. Маса блока m 100 кг , коефіцієнт сухого тертя k 0,2 .
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
Розв’язування. |
Роботу будемо шукати за формулою (5.20) |
A12 Fdrтерт ds . Оскільки сила тертя є |
|||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kN |
|
|
|
|
|
|
|
||||
F ковз |
|
, |
а |
|
dr |
, то її проекція |
F терт |
на dr |
завжди від’ємна, |
F терт kN , |
то |
|
|
|
|||||||||||
тертя |
|
|
|
|
dt |
dr |
|
|
dr |
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
2 |
2 |
|
|
|
|
|
||
A12 ( kN )ds kmgds kmg ds kmgs12 |
, причому було враховано, що N mg . Ми бачимо, |
що |
||||||||||
|
1 |
|
|
1 |
1 |
|
|
|
|
|
||
143
шукана робота завжди від’ємна за знаком, а за абсолютною величиною прямо пропорційна довжині пройденого тілом шляху. Перше означає, що для того, щоб переміщення тіла відбувалося зі сталою за
модулем швидкістю const , якій відповідає кінетична енергія T m 2  2 , яка також повинна бути
2 , яка також повинна бути
сталою, необхідно компенсувати втрату кінетичної енергії тіла T за рахунок від’ємної роботи сили тертя такою ж за величиною додатною роботою. Якщо, згаданий блок живлення перетягують люди, то це робота сил, що прикладені до блоку з боку людей, які тягнуть або штовхають цей блок. Для того, щоб мінімізувати цю роботу, треба мінімізувати шлях: тягти блок із кутка в куток по діагоналі квадрата. При
цьому необхідно |
виконати |
|
роботу A |
|
0,2 100 кг 9,81 м с 2 |
10 |
|
|
м |
= 2746 Дж. Якщо, |
|||||||||||||||||||||||||||||||
|
|
2 |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
наприклад, перетягування здійснити за 15 секунд, то середня потужність складе N =183 Вт. |
|||||||||||||||||||||||||||||||||||||||||
|
Приклад 2. Нехай частинка з масою |
|
m1 |
переміщується з точки 1 в точку 2 по деякій траєкторії |
|||||||||||||||||||||||||||||||||||||
неподалік від частинки з масою |
m2 , |
що знаходиться в точці O . Обчислити роботу гравітаційної сили |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
m1m2 r |
при такому переміщенні частинки m1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
r 2 |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Розв’язування. Використовуючи (5.20) запишемо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
2 |
rdr |
|
2 |
dr |
|
|
|
|
|
1 |
|
1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
rdr |
|
|
|
|
|
|
|
|||||||||||||||||||
|
A |
|
|
|
Fdr |
|
|
|
|
|
|
|
dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||
|
|
r 2 r |
|
|
r3 |
|
|
r3 |
r 2 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
r |
|
r |
|
r |
|
|
||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
2 |
|
1 |
|
1 |
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
або, остаточно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
A |
Gm m |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.23) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
12 |
|
|
|
|
1 |
2 r |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rdr .1 |
|||
|
При обчисленні інтеграла (5.13) було використано корисну рівність rdr |
|
|||||||||||||||||||||||||||||||||||||||
Необхідно відзначити, що обчислена нами у Прикладі 2 робота A12 залежить лише від
положення початкової та кінцевої точок траєкторії. Це означає, що вона зовсім не залежить від форми траєкторії. Цей факт пов’язано зі спеціальними властивостями сили гравітаційної взаємодії. Зауважимо, що не всі сили мають такі властивості. Обчислена нами робота може
бути як додатною, так і від’ємною: якщо r1 r2 , то A12 |
0 , а якщо r1 |
r2 , то A12 0 . |
|
|||||||||
У літературі можна зустріти вирази: «робота сил поля» (коли A12 0 ) або «робота проти сил |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
поля» (коли |
A12 0 ). Також використовують вирази: |
«робота сили F |
на деякому шляху», |
якщо |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 Цю рівність можна одержати виходячи з очевидної рівності r 2 |
|
|||||||||||
(r |
r ) Дійсно, можна записати d(r 2 ) d(r |
r ) , звідки |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
2rdr dr |
r |
r |
dr |
2rdr |
, тобто rdr rdr . |
|
|
|
|
|
||
