
5_Zakony zberezhennia
.pdf164
швидкість центру мас (системи як цілого) VC const . Зокрема, це має місце для замкненої
системи частинок: центр мас замкненої системи частинок рухається рівномірно і прямолінійно,
так само, як відбувається вільний рух частинки. Згадаємо, що вільний рух частинки це такий рух, при якому частинка не взаємодіє з іншими матеріальними об’єктами, а замкнена система частинок – це така, частинки якої не взаємодіють з матеріальними об’єктами, що лежать поза системою. З цієї точки зору рух системи частинок як цілого подібний до руху однієї частинки
змасою, що дорівнює масі системи, під дією зовнішніх щодо системи сил.
Узагальному випадку імпульс системи частинок змінюється при переході від однієї
системи відліку до іншої. Нехай в деякій системі відліку K імпульс системи частинок
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
mi i . |
При |
переході |
до |
системи |
відліку |
K , що рухається |
поступально |
відносно |
|||||
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
системи |
відліку |
K із швидкістю V , швидкість i -тої частинки в системі відліку |
K можна |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
подати як i i V , а імпульс системи частинок, визначений в системі відліку K , відповідно |
||||||||||||||
як |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
n |
|
|
|
|
|
|
P |
mi (i V ) |
mi i miV |
P MV . |
|
(5.76) |
||||||||
|
|
i 1 |
|
|
|
i 1 |
|
i 1 |
|
|
|
|
|
|
|
або з врахуванням (5.74) |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MVC |
P |
MV , |
|
|
|
|
|
|
|
(5.77) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
K . Таким чином, при |
|
|
де |
P |
– |
імпульс системи частинок визначений в системі відліку |
||||||||||
такому переході зміна імпульсу дорівнює добутку маси системи на відносну швидкість однієї
|
|
|
системи відліку відносно іншої. З останньої рівності (5.77) видно, що коли V |
VC , |
то P 0 , |
тобто імпульс системи частинок визначений у системі відліку, в якій центр мас системи
частинок знаходиться в спокої, завжди дорівнює нулю. Цей факт випливає й безпосередньо
з формули (5.74), де треба покласти VC рівним нулю. Таку систему відліку називають
системою центру мас (СЦМ). Зауважимо, що СЦМ для замкненої системи частинок завжди є інерціальною системою відліку, для незамкненої – в загальному випадку неінерціальною.
Система центру мас – це система відліку, в якій система частинок як ціле знаходиться в спокої.
165
Таку систему відліку називають також власною системою відліку системи частинок. Рух частинок відносно СЦМ називають внутрішнім рухом системи частинок. Рух системи частинок відносно довільної системи відліку завжди можна розглядати як суперпозицію
|
|
|
|
|
|
|
внутрішнього руху і руху системи як цілого, що відбувається зі швидкістю VC . |
||||||
Зокрема, імпульс |
системи |
частинок, |
визначений у деякій системі |
відліку K можна |
||
|
|
|
|
n |
|
|
|
~ |
MVC , |
~ |
|
~ |
|
подати у вигляді P P |
де P |
mi i (t) – імпульс системи частинок, пов’язаний з її |
||||
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
~ |
(t) – швидкості частинок системи в СЦМ, а MVC |
– імпульс системи |
|||
внутрішнім рухом, а i |
||||||
частинок, пов’язаний з її рухом як цілого.
Як уже було показано вище, внесок внутрішнього руху в імпульс системи частинок
|
n |
~ |
|
завжди дорівнює нулю, P |
|
|
i 1 |
~
mi i (t) 0 . З цього випливає, що імпульс системи не може
бути змінений за рахунок внутрішніх рухів частинок або, що теж саме, за рахунок внутрішніх сил.
Відповідно до принципу відносності механіки, якщо імпульс системи частинок зберігається в одній ІСВ, то він буде зберігатися і в усіх інших ІСВ. Це можна показати й
|
|
|
|
безпосередньо. |
Нехай в ІСВ K імпульс системи частинок зберігається, P const . Нехай ІСВ |
||
K рухається відносно системи |
|
const . Тоді з рівняння (5.73) випливає, |
|
K зі швидкістю V |
|||
|
|
|
|
що P const , |
оскільки P const і MV const . |
|
|
Зауважимо, що рівняння (5.66) та (5.75) можуть бути застосовані і в НеІСВ, але тоді прикладені до частинок сили інерції необхідно розглядати як зовнішні з огляду на те, що для сил інерції не можна вказати джерела всередині системи частинок. Це, в свою чергу, означає,
що в НеІСВ не існує замкнених систем частинок.
5.2.2 Рух тіла змінної маси
Існує багато випадків, коли маса тіла, що рухається, змінюється неперервним чином у процесі його руху. Маса більшості транспортних засобів зменшується під час руху за рахунок зменшення запасу палива, причому найбільш істотним таке зменшення є для літаків та ракет. У

166
деяких ситуаціях маса зменшується за рахунок висипання чи витікання якихось речовин з борту транспортного засобу: наприклад, розсипання добрива чи розпилення хімікатів при сільськогосподарських роботах або виливання води при гасінні лісових пожеж з літаків та гелікоптерів. Але маса так само може зростати, наприклад, при дозаправці літака під час польоту або при навантаженні платформи сипучим матеріалом під час її руху. У
найзагальнішому випадку одночасно мають місце процеси від’єднання деякої маси та приєднання деякої іншої за величиною маси до тіла, що рухається. При цьому відносні швидкості мас, які приєднуються і від’єднуються від тіла, що рухається, можуть бути самими різним як за величиною, так і за напрямом. Наприклад, при насипанні піску з бункера на платформу, що рухається, і одночасному висипанні його через дірку в платформі напрями руху маси, що приєднується, маси, що від’єднується, перпендикулярні до напрямку руху тіла
(платформи) (Рис. 5.12). При нульовій відносно тіла швидкості приєднання або від’єднання маси збільшується або зменшується маса тіла, але при цьому разом з цими масами тілу імпульс не передається і від нього не забирається. При польоті літака з повітряно-реактивним двигуном приєднання і від’єднання мас відбувається, як правило, в напрямку колінеарному з рухом літака і зі значними відносними (щодо літака) швидкостями, завдяки чому необхідно враховувати не лише збільшення або зменшення маси тіла (літака) при приєднанні й від’єднанні мас, але й набуття ним і втрату імпульсу, який переноситься масами, що приєднуються та від’єднуються.
Рівняння Мєщєрського. Ми розглянемо найбільш загальний випадок руху тіла змінної маси, коли має місце одночасне приєднання й від’єднання мас з різними ненульовими швидкостями відносно тіла змінної маси, схематично зображене на Рис. 5.12.
|
|
|
2 |
|
1 |
|
|
|
|
u 2 |
u1 |
m2 |
m |
m1 |
Рис. 5.12. До руху тіла змінної маси.

167
Рух тіла змінної маси можна розглядати як рух деякої системи частинок як цілого, що описується рівнянням (5.66)
dPdt F зовн .
Обчислимо приріст імпульсу тіла dP |
за елементарний проміжок часу dt . |
Нехай в |
||
|
|
|
|
m dm , а |
момент часу t імпульс тіла є P m(t) (t) . У момент часу t dt маса тіла стане |
||||
його швидкість відносно деякої |
ІСВ стане |
|
|
|
d . Окрім цього, треба врахувати зміну |
||||
імпульсу тіла за елементарний проміжок часу dt , пов’язану з набуттям і втратою імпульсу
внаслідок від’єднання та приєднання елементарних мас dm1 та dm2 , відповідно, що мають
|
|
|
|
|
|
|
|
|
|
швидкості 1 та 2 відносно вищезгаданої ІСВ: 1dm1 2 dm2 |
. Таким чином, імпульс тіла в |
||||||||
момент часу t dt буде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P(t dt) |
(m dm)( d ) 1dm1 2 dm2 . |
|
(5.78) |
|
|||||
Оскільки сума маси тіла |
|
m(t) , |
маси речовини, яка вже від’єдналася від тіла, |
m1 (t) та |
|||||
речовини, яка |
може приєднатися |
до тіла |
в майбутньому, |
m2 (t) зберігається, |
тобто |
||||
m(t) m1 (t) m2 (t) const , |
існує |
зв’язок |
між |
елементарними приростами |
цих |
мас |
|||
dm dm1 dm2 |
0 , звідки знаходимо |
|
|
|
|
|
|||
dm dm1 dm2 . |
|
|
|
|
|
|
(5.79) |
||
Після підстановки (5.79) до (5.78) і елементарних перетворень нехтуючи нескінченно
малою другого порядку dmd отримаємо
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P(t dt) (m dm1 dm2 )( d ) |
1dm1 |
2dm2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||
m md dm1 |
( 1 ) dm2 ( 2 ) |
|
|
|
|
|
|||||||||||||||
Отже, шуканий приріст імпульсу тіла є |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
dP P(t dt) P(t) |
m md dm1 |
( 1 ) |
dm2 ( 1 ) m |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
md dm1 ( 1 ) dm2 |
( 1 ). |
|
|
|
|
|
|
||||||||||||
Після підстановки знайденого приросту до (5.66) одержуємо |
|
||||||||||||||||||||
|
|
|
|
dm |
|
|
|
|
dm |
|
|
|
|
|
|
|
|
|
|
||
|
d |
|
|
|
2 |
зовн , |
|
|
|
|
|
||||||||||
m |
|
|
|
|
1 |
( ) |
|
|
|
( |
|
) F |
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||
|
|
dt |
|
dt |
|
1 |
|
|
dt |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(5.80)
(5.81)
(5.82)

|
|
|
|
|
|
|
|
|
|
|
168 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де |
( 1 ) |
та (2 |
) є ніщо інше як швидкості елементарних мас dm1 |
та dm2 , відносно |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
тіла, |
що рухається зі швидкістю , які ми |
позначимо, відповідно, як |
u1 (1 ) та |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
u2 |
(2 |
) . |
|
|
|
|
|
|
|
||
|
|
Наприклад, у випадку літака з повітряно-реактивним двигуном, показаного на Рис. 5.13, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
, |
1 |
, 2 – це, відповідно, швидкості літака, газів, які щойно від’єдналися від літака, і повітря, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
яке приєднається до літака, визначені відносно землі, u1 |
– швидкість витікання газів із сопла |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
реактивного |
двигуна |
літака, а u2 – швидкість, |
з якою |
повітря набігає на |
вхідний |
отвір |
|||||
реактивного двигуна.
Тоді (5.82) можна переписати так
|
|
|
|
dm |
|
|
dm |
|
|
|
|
|
d |
зовн |
|
|
|
||||||
m |
|
F |
1 |
u |
|
2 |
u |
|
. |
(5.83) |
|
|
|
|
2 |
||||||||
|
dt |
|
|
dt |
1 |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Це основне диференціальне рівняння поступального руху тіла змінної маси для випадку одночасного приєднання та від’єднання частинок називається рівнянням Мєщєрського.
Величину
|
dm |
|
dm |
2 |
|
|
|
|
|
|
1 |
u |
|
u |
|
|
|
(5.84) |
|
|
|
|
2 |
|
|
||||
|
dt |
1 |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
називають реактивною силою. |
|
||||||||
|
повітря |
|
|
|
|
|
|
|
|
|
|
m2 |
|
|
|
m |
|
гази |
m1 |
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
1 |
|
|||
Рис. 5.13. До руху реактивного літака
Хоча рівняння Мєщєрського (5.83) за і формою збігається з основним рівнянням динаміки частинки (добуток маси тіла, рух якого розглядається, на його прискорення дорівнює сумі всіх сил, що діють на нього з реактивною силою включно), необхідно пам’ятати, що його ліва частина в загальному випадку не може бути подана, як похідна за часом від добутку маси тіла

|
|
|
|
|
|
169 |
|
|
|
|
|
|
|
|
|
d |
|
d (m(t) ) |
|
|
m(t) |
на його швидкість (t) , оскільки |
m(t) |
|
|
, причому саме ця нерівність |
|
dt |
dt |
зумовлює наявність реактивної сили. Сама реактивна сила є по своїй суті силою реакції,
прикладеною до тіла з боку маси, що від’єднується від тіла або приєднується до нього з ненульовою швидкістю, звідки й походить назва сили.
За відсутності реактивної сили рівняння (5.83) набуває вигляду
d зовн
m(t) dt F .
Така ситуація виникає, наприклад, у випадку руху платформи(Рис. 5.14), з якої вільно (з
|
|
0 |
|
dm |
2 |
0 . |
нульовою початковою відносною швидкістю) висипається пісок, тобто |
u |
і |
|
|||
|
|
|||||
|
1 |
|
|
dt |
|
|
|
|
|
|
|
|
Якщо ж на платформу, що рухається в горизонтальному напрямку зі швидкістю , з
нерухомого бункера насипається пісок (Рис. 5.14), то оскільки горизонтальна складова його
|
|
швидкості відносно платформи u2 |
, то виникає |
реактивна сила, яка діє на платформу в горизонтальному
|
|
|
dm |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
напрямку, |
|
|
|
, |
напрямлена |
протилежно |
швидкості |
|||||||||
|
dt |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
dm |
2 |
0 . Так як |
|
dm , то |
||
платформи , |
оскільки |
|
|
dm |
||||||||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рівняння (5.83) набуває вигляду |
|
|
|
|
||||||||||||
|
|
|
|
|
dm |
або |
|
|
|
|||||||
m d |
F зовн |
d (m ) F зовн , |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dt |
|
|
|
гор |
|
dt |
|
|
|
|
dt |
гор |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
m2
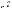
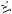



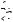
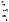






 m
m 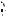
 m1
m1
Рис. 5.14. До руху тіла змінної маси
де Fгорзовн – горизонтальна складова зовнішніх сил, що діють на платформу.
Як і слід було чекати, внесення маси під знак похідної, яке привело рівняння руху платформи до вигляду повністю ідентичному основному рівнянню динаміки частинки,
призвело до зникнення з цього рівняння реактивної сили у явному вигляді внаслідок її
«заховування» до похідної d (m ) . dt
170
За допомогою рівняння Мєщєрського (5.83) можна розглянути широке коло практично важливих задач, серед яких рух літака з повітряно-реактивним двигуном та рух ракети у вільному просторі, які ми розглянемо нижче.
Рух реактивного літака. При всій різноманітності повітряно-реактивних двигунів, якими оснащено реактивні літаки, всі вони тим чи іншим чином приєднують (засмоктують)
атмосферне повітря і викидають (відокремлюють) продукти згоряння. (Рис. 5.13). При застосуванні рівняння Мєщєрського (5.83) до руху реактивного літака можна вважати, що маса літака залишається сталою, оскільки секундна витрата палива мала порівняно з повною масою
літака, тобто dm (dm1 |
dm2 ) 0 , звідки |
dm1 dm2 . Підкреслимо, що завжди |
dm1 0 , |
||||||||
оскільки маса викинутих газів може лише зростати. Тоді рівняння (5.83) набуває вигляду |
|||||||||||
|
|
|
dm |
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|||||
m |
|
F зовн |
1 |
|
(u |
u |
) , |
|
|
|
(5.85) |
|
|
|
|
|
|
||||||
|
dt |
|
dt |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Для літака, що перебуває в польоті, сума зовнішніх сил є F |
зовн mg |
R , де |
R – сила |
||||||||
реакції з боку повітря, яку можна подати як суму так званої сили лобового опору літака та
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
підйомної сили крила літака, |
R F під F лоб. оп. , які буде докладно розглянуто в Розділі 7. |
||||||||||||||||
|
|
|
|
|
|
dm |
|
|
|
|
|
|
|
|
|
||
Щодо реактивної |
сили |
|
|
|
1 |
(u |
u |
|
) , |
то її |
величина і |
напрямок визначаються темпом |
|||||
|
|
|
2 |
||||||||||||||
|
|
|
|
|
|
dt |
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
відділення маси |
|
1 |
та величиною та напрямками векторів |
u |
та u |
|
. У переважній кількості |
||||||||||
|
|
2 |
|||||||||||||||
|
|
dt |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
випадків обидва вектори |
u1 |
та |
u2 |
направлені |
протилежно до |
вектора швидкості літака |
|||||||||||
(Рис. 5.13), причому реактивна сила направлена в напрямку руху літака тоді, коли u1 u2 ,
тобто швидкість витікання продуктів згоряння більша за швидкість потоку повітря відносно реактивного двигуна.
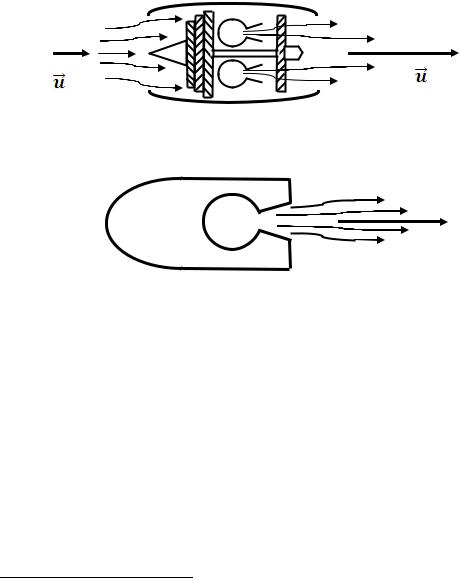
У найбільш розповсюдженому з повітряно-реактивних двигунів так званому турбореактивному двигуні (Рис. 5.15а) повітря надходить до двигуна через вхідний отвір 1 і його тиск підвищується компресором 2, вал якого обертається газовою турбіною 4, встановленою в потоці продуктів згоряння, які розширюються на виході камери згоряння 3 і викидаються з двигуна через сопло 5 зі швидкістю u2 , яка перевищує швидкість u1 .
171
Реактивну силу, що виникає при роботі реактивного або ракетного двигуна називають силою тяги і
вимірюють у ньютонах або ж у кілограмах сили, 1 кгс 9,81 Н , а для великих двигунів, відповідно, в
кілоньютонах або в тонах сили. Слід підкреслити, що сила тяги є більш адекватною характеристикою реактивних двигунів, ніж потужність, якою прийнято характеризувати поршневі двигуни внутрішнього згоряння, парові турбіни, електродвигуни тощо. Це пов’язано з тим, що реактивний двигун фактично поєднує в собі функцію власне двигуна (електродвигун, парова машина або турбіна, двигун внутрішнього згоряння тощо), який перетворює енергію різних видів (електричну, теплову, хімічну тощо) в механічну енергію (роботу) і рушія (рушійного пристрою, наприклад, ведучого колеса, гусениці, водяного ґвинта чи
а
|
|
4 |
|
m2 |
3 |
|
m1 |
|
5 |
||
1 |
|
|
|
|
|
|
|
2 |
3 |
|
1 |
2 |
|
|
|
|
|
|
б
m1
3 5
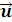 1
1
Рис. 5.15. Турбореактивний (а) та ракетний (б) двигуни.
повітряного пропелера3 тощо), який забезпечує перетворення механічної енергії двигуна в роботу по пересуванню транспортного засобу. Так звану статичну силу тяги реактивного двигуна вимірюють на спеціальних вимірювальних стендах, де сила тяги двигуна врівноважується іншою відомою силою
(наприклад, силою пружності динамометра). За таких умов двигун не рухається і його потужність дорівнює нулю, незалежно від величини його сили тяги.
Натомість у літаках з таким рушієм як повітряний ґвинт, двигун, що обертає цей ґвинт, завжди виконує роботу по обертанню згаданого ґвинта, незалежно від того рухається літак чи стоїть нерухомо на
3Термін propeller в англійській мові взагалі означає «рушій». Він застосовується до будь-яких рушіїв, а не лише, майже виключно, до повітряних ґвинтів, як , наприклад, в українській або російській мові.

172
гальмах або на випробувальному стенді. За рахунок цієї роботи здійснюється прискорення деякої маси повітря, яка проходить через уявну трубу з діаметром, що дорівнює діаметру ґвинта, тобто надання цій масі
|
|
імпульсу |
|
|
, внаслідок чого |
виникає сила тяги |
|
певної швидкості u |
відносно ґвинта, а отже й |
p mu |
|||||
|
|
|
потоку повітря за одиницю часу. |
Ця сила тягне (або |
|||
F |
dp dt , що визначається імпульсом наданим |
||||||
штовхає) літальний апарат у напрямку протилежному швидкості потоку повітря u . Таким чином, дія
рушійної установки, обладнаної повітряним ґвинтом (пропелером), який обертається поршневим або газотурбінним двигуном, з точки зору механіки нічим не відрізняється від дії реактивного рушія: в обох випадках сила тяги, що рухає літальний апарат, виникає за рахунок прискорення потоку газів відносно літального апарату і являє собою силу реакції, яка передбачається третім законом Ньютона.
Необхідно відзначити, що одна й та сама сила тяги може бути створена при передачі повітряному потоку деякого імпульсу за одиницю часу p mu , але при різних співвідношеннях маси m і швидкості u
повітряного потоку прискорюваного пропелером. Оскільки робота, яку виконує повітряний ґвинт за
одиницю часу, є енергія m 2 / 2 , яка передається ґвинтом повітряному потоку за одиницю часу, то ясно, що
витрати енергії для створення однієї й тієї ж сили тяги менші, коли більша маса повітря відкидається ґвинтом з меншою швидкістю. Розглянемо простий приклад. При відкиданні ґвинтом за одну секунду маси
повітря 10 кг зі швидкістю u 100 м / с повітряному потоку щосекунди передається імпульс
p 1000 кг м / с , що відповідає силі тяги 1000 Н . Така сама величина сили тяги може бути забезпечена при
відкиданні ґвинтом за одну секунду маси повітря 100 кг зі швидкістю |
u 10 м / с . Але робота, що |
виконується ґвинтом щосекунди, у першому випадку становить 1 2 10 1002 |
50 кДж , а у другому – лише |
1 2 100 102 5 кДж , тобто на порядок менше! Зрозуміло, що при одній і тій самій потужності двигуна його статична сила тяги буде тим більша, чим більша маса повітря, що відкидається ґвинтом. Тому несучий ґвинт гелікоптера, який має забезпечити силу тяги більшу за вагу гелікоптера, має великий діаметр і порівняно повільно обертається, а діаметри тягнучих ґвинтів літаків значно менші і обертаються вони зі значно більшої швидкістю.
2 100 102 5 кДж , тобто на порядок менше! Зрозуміло, що при одній і тій самій потужності двигуна його статична сила тяги буде тим більша, чим більша маса повітря, що відкидається ґвинтом. Тому несучий ґвинт гелікоптера, який має забезпечити силу тяги більшу за вагу гелікоптера, має великий діаметр і порівняно повільно обертається, а діаметри тягнучих ґвинтів літаків значно менші і обертаються вони зі значно більшої швидкістю.
Потужність, яку розвиває реактивний двигун залежить від його швидкості. Так, двигуни одного з найбільших у світі пасажирських літаків Боїнг-747-200 у горизонтальному польоті на висоті 12,2 км зі сталою швидкістю 265 м / c створюють силу тяги F 245 кН , що складає лише чверть від їх сумарної
статичної сили тяги. Їх сумарна потужність при цьому складає 65 тис. кВт або 87 тис. к. с. Цієї потужності достатньо, щоб компенсувати втрати енергії літака на подолання сили опору повітря. Але при наборі висоти
173
і при розгоні літака двигуни працюють з повною тягою, оскільки виконують додаткову роботу, яка йде на збільшення потенціальної енергії літака в полі тяжіння землі, а також на збільшення його кінетичної енергії.
Рух ракети. Розглянемо рух ракети у вільному просторі, тобто за відсутності зовнішніх сил зумовлених наявністю оточуючого середовища (наприклад, повітря) або силових полів. Оскільки рух ракети забезпечується викиданням у вільний простір робочого тіла (звичайно, газоподібних
продуктів горіння ракетного палива) з деякою відносною швидкістю u1 (відокремлення маси)
(Рис. 5.15б), а приєднання маси до ракети відсутнє, то в рівнянні Мєщєрського (5.83) треба
покласти dm2 |
0 |
і врахувати, що в цьому випадку dm1 dm . Тоді |
рівняння руху ракети |
|||
набирає вигляду |
|
|
||||
|
|
dm |
|
|||
|
d |
|
||||
m |
|
|
|
u |
, |
(5.86) |
dt |
dt |
|||||
де dm 0 , оскільки маса ракети зменшується внаслідок відділення від неї робочого тіла.
Вектор прискорення, якого набуває ракета, направлений протилежно вектору відносної швидкості
відділення робочого тіла u .
Рівняння руху ( 5.86) можна записати у вигляді
|
dm |
|
|
d |
|
u |
(5.87) |
m |
|||
|
|
|
|
|
|
|
|
|
|
|
m0 вважаючи, що швидкість |
і проінтегрувати при початкових умовах (0) |
0 , |
m(0) |
|||||||||
витікання газів відносно ракети стала, u const : |
|
|
|
||||||||
|
|
|
m dm |
|
|
|
|
||||
|
|
|
|
|
|
||||||
d |
u |
|
|
|
, |
|
|
(5.88) |
|||
m |
|
|
|||||||||
0 |
|
|
m |
|
|
|
|
||||
|
|
|
|
|
0 |
|
|
|
|
|
|
звідки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
||
u ln |
|
0 |
. |
|
|
|
(5.89) |
||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рівність (5.89) можна спроектувати на напрям швидкості |
, а потім переписати у формі |
||||||||||
|
m0 |
|
|
|
|
|
|
|
|
|
|
|
eu . |
|
|
|
|
|
|
(5.90) |
|||
|
m |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
