Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Киевский национальный университет им. Т. Шевченко

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

5_Zakony zberezhennia

.pdf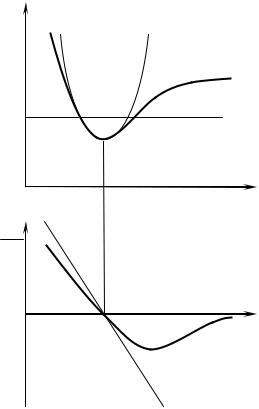

Скачиваний:

Добавлен:

19.03.2015

Размер:

1.39 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 87 8 > Следующая >>>

194

Перенесемо для зручності початок відліку в точку x0 мінімуму функції U (x) . Тоді в

точці мінімуму x0 0 і (142) можна переписати у вигляді

U (x)

1 d 2U

kx2

(5.143)

2 dx2

X 0

d 2U

де введено

позначення

dx2

X 0

покладено U (0) 0 , тобто потенціальна енергія

відраховується від її значення в мінімумі.

Таким чином, при малих зміщеннях від положення рівноваги (мінімуму потенціальної енергії) потенціальна енергія частинки залежить

від зміщення квадратично
U (x)	kx2	,	(5.144)
	2

а сила, що прикладена до частинки, є

U(x)

0x0

dUdx

F(x)

0 x0

F (x)	dU	kx ,	(5.145)	Рис. 5.20. До малих коливань частинки
	dx

тобто залежить від зміщення лінійно.

На Рис. 5.20 суцільними кривими подано графіки функції потенціальної енергії U (x) та

відповідної до неї сили F(x) , а штриховими лініями їх апроксимації в наближенні малих

коливань. Відповідно, при малих коливаннях для параболою для U (x) маємо параболу з

вершиною в точці мінімуму U (x) , а для сили F(x) пряму, що перетинає вісь абсцис в точці

мінімуму (в положенні рівноваги) .

Таким чином, рух частинки поблизу мінімуму потенціальної енергії є рухом під дією квазіпружної сили, який, як було показано раніше у Розділі 3, є гармонійним рухом. Період такого руху може бути знайдений безпосередньо із загального виразу для періоду фінітного руху (5.140)

195

kx2

sin 2 z

cos z dz

T 2

sin z

kx2

)

1 sin

cos z dz

dz 2

m k .

(5.146)

Знайдений

вираз

для

періоду

малих

коливань

співпадає

з результатом, отриманим

розв’язуванням відповідного рівняння руху частинки під дією квазіпружної сили (див. формулу

(3.43) Розділу 3) . Відповідна циклічна частота є 0 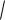k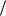m . У наближенні малих коливань

поблизу положення рівноваги їх період не залежить від амплітуди коливань. Але при застосуванні формули треба завжди пам’ятати, що вона отримана для наближення малих коливань.

Наближення малих коливань частинки поблизу положення рівноваги, якому відповідає гармонійний рух x(t) x0 cos(0t) (завдяки цьому його іноді називають гармонійним

наближенням) відіграє визначну роль у механіці і в фізиці взагалі, тому що величезна кількість фізичних систем має положення рівноваги в мінімумі потенціальної енергії, яку поблизу мінімуму завжди можна апроксимувати параболою.

Добираючи спеціальна форму U (x) можна отримати так звані ізохронні коливання поблизу

мінімуму потенціальної енергії, тобто такі період яких не залежить від величини відхилення.

5.6.3 Стаціонарна течія ідеальної рідини

Застосуємо рівняння (5.133) до розгляду ламінарної стаціонарної течії ідеальної рідини в

полі сили тяжіння Землі.				Трубка току
				Трубка току
Виділимо в рідині трубку току,
як показано на Рис. 5.21, а в			ній		Δℓ1
					Δℓ1
деякий об’єм рідини, що лежить між
двома	поперечними	перерізами,			Δℓ2
двома	поперечними	перерізами,			S1
					S1
площі яких s1 та s2 (заштриховано з				h1	S2
				h1	S2
нахилом вправо) . Нехай за деякий					h2
нахилом вправо) . Нехай за деякий
проміжок часу t маса рідини,			що	Рис. 5. 21. Стаціонарна течія ідеальної рідини
				Рис. 5. 21. Стаціонарна течія ідеальної рідини

196

містилась у цьому об’єм, переміщується вдовж трубки току в положення 2 (заштриховано з

нахилом вліво). Зовнішнє однорідне поле тяжіння є стаціонарним полем, отже U 0 . Рідина

є ідеальною, отже 1) в ній відсутні сили внутрішні дисипативні сили (сили внутрішнього тертя,

які зумовлюють в’язкість); 2) рідина нестислива, тобто відстань між її частинками не

змінюється, отже не змінюється і її внутрішня потенціальна енергія, U const . Таким чином,

у цьому випадку рівняння (5.133) для розглядуваної кількості рідини набуває вигляду

dT U U	N зовн.неконс .	(5.146)
dt

Зміну повної механічної енергії в полі сили тяжіння розглядуваної кількості рідини за

проміжок часу t можна подати у вигляді

E E			E A			,	(5.147)
		2		1	12
де	E	та	E	повні механічні енергії розглядуваної кількості рідини			в положеннях 1 та
	1		2

2, відповідно, A12 робота зовнішніх неконсервативних сил по переміщенню цієї кількості

рідини з положення 1 в положення 2. З Рис. 5.26 видно, що ця зміна енергії може бути знайдена

як різниця енергій e2 та e1 малих об’ємів рідини s2 l2 та s1 l1 , оскільки ділянка трубки току,

заштрихована перехресно, є спільною для обох положень. Переміщення розглядуваної

кількості рідини вздовж трубки току відбувається під дією сторонніх сил гідростатичного

тиску, причому робота тих з них, що діють на бокові стінки трубки току дорівнює нулю,

оскільки ці сили перпендикулярні напряму переміщення рідини в трубці току. Таким чином,

E e2 e1 p1s1 l1				p2 s2 l2 .				(5.148)
Отже,		з	врахуванням		умови	неперервності течії, рідини, що		не стискається,
s1 l1 s2 l2		V , можна записати
	( V ) 2				( V ) 2
		2	( V )gh2		1	( V )gh1	( p1 p2 ) V ,	(5.149)
	2				2

або остаточно

197

	2					2
	2	gh	p			1	gh p .		(5.150)
		gh	p	2			gh p .		(5.150)
2	2			2	2	1		1
2					2
Отже, для будь-якого якого перерізу трубки току
	2	gh p const .							(5.151)

2
2

Це рівняння називається рівнянням Бернуллі.

5.6.4 Зіткнення частинок

Застосуємо закони збереження до задачі про зіткнення частинок. Під зіткненням двох частинок розуміють такий процес, що відбувається за відсутності впливу інших матеріальних об’єктів, результатом якого є зміна початкових швидкостей частинок, які вони мали перебуваючи на великій відстані одна від одної, внаслідок взаємодії частинок між собою.



а	1		б
а		2	б

Рис. 5.22. Зіткнення частинок

Нехай дві частинки з масами m1 та m2 спочатку знаходяться на великій відстані одна від

одної (Рис. 5.22) і мають, відповідно, швидкості 1 та 2 . Під великою відстанню ми розуміємо

таку відстань, коли взаємодія між частинками настільки мала, що нею можна знехтувати і рух частинок вважати вільним, а, отже, прямолінійним і рівномірним. При цьому повна механічна енергія системи частинок визначається виключно їх кінетичними енергіями. При зменшенні відстані між частинками взаємодія між ними зростає і зростає сила, що прикладена до кожної із частинок з боку іншої частинки, а внаслідок цього виникає прискорення кожної частинки,

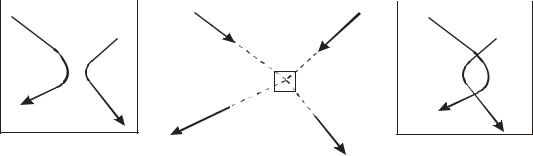
тобто вектори швидкостей змінюються за модулем та за напрямком. Залежно від того, які сили діють між частинками відштовхування чи притягання, траєкторії частинок в області

198

простору, де відстань між ними мінімальна, проходять по-різному, як то схематично зображено, відповідно, на вставках а і б Рис. 5.22. Але якщо подивитися на процес зіткнення з великої відстані, то ця різниця непомітна і створюється таке враження, начебто частинки,

вдарившись одна об одну, розлітаються в різних напрямках зі швидкостями та .

1 2

Зауважимо, що зіткнення частинок не обов’язково означає їх безпосередній контакт, як це має місце, наприклад, при зіткненні більярдних куль або інших макроскопічних об’єктів. У таких випадках говорять про так звану контактну взаємодію тіл, яка на мікроскопічному рівні здебільше зводиться до електромагнітної. Задача про зіткнення частинок полягає у знаходженні швидкостей частинок після зіткнення, тобто після того, як частинки знову розійдуться на значну відстань, на якій взаємодією між ними можна знову нехтувати і їх швидкості усталяться.

Для замкненої системи частинок завжди і, зокрема, при зіткненні двох частинок,

виконуються закони збереження імпульсу та збереження моменту імпульсу (тут і надалі штрихами позначено величини після зіткнення):

												(5.152)
p	p	2	p p									(5.152)
1		2	1		2
											] .	(5.153)
[r	p ]		[r	p	2	] [r	p ] [r p				] .	(5.153)
1	1		2		2	1		1	2	2
Що стосується						повної		механічної			енергії E	при зіткненні двох частинок, то вона

зберігається не завжди. Розрізняють так звані абсолютно пружні зіткнення, при яких повна механічна енергія E зберігається, тобто повна механічна енергія системи двох частинок після

зіткнення E дорівнює повній механічній енергії цієї системи до зіткнення, E E , та

непружні зіткнення, внаслідок яких повна механічна енергія зменшується, E E . Причинами такого зменшення можуть бути, наприклад, зміна внутрішньої енергії частинок в процесі зіткнення або перетворення механічної енергії в інші види енергії, наприклад, в енергію електромагнітного поля при зіткненні заряджених частинок.

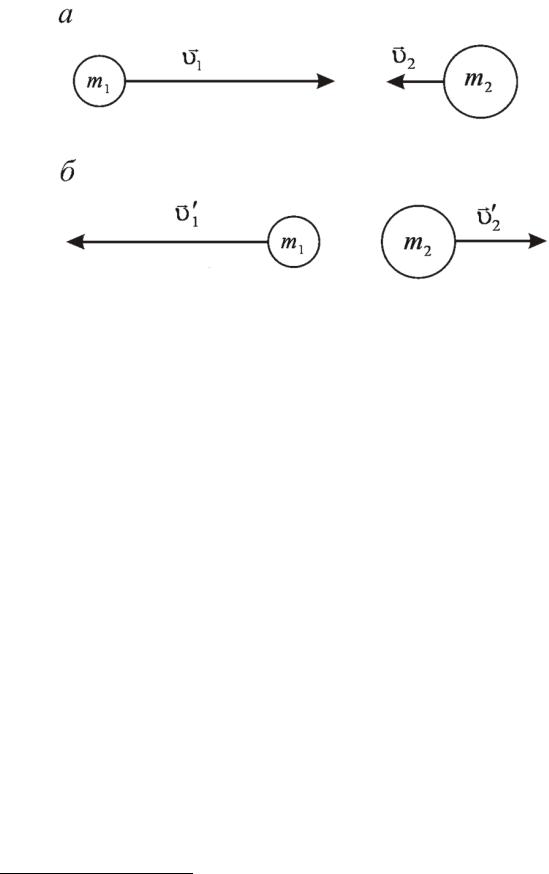
Лобові зіткнення частинок. Найпростішим є випадок так званих лобових зіткнень, коли до і після зіткнення обидві частинки рухаються по траєкторіям, що повністю лежать на одній прямій (Рис. 5.22).

199

Рис. 5.22. Лобове зіткнення частинок

Розглянемо спочатку граничний випадок непружного зіткнення, так зване абсолютно непружне лобове зіткнення, після якого частинки не «відскакують» одна від одної, а рухаються разом10. На Рис. 5.22а показано рух двох частинок перед лобовим зіткненням.

Скористаємося законом збереження імпульсу у формі

			,
m1 1	m2 2	(m1 m2 )	,	(5.154)

де враховано, що за означенням абсолютно непружного зіткнення обидві частинки після

зіткнення рухаються разом, тобто з однаковою швидкістю , яку знаходимо з (5.154):


	m	m
	1 1	2 2	.	(5.155)

	m1 m2

Легко бачити, що знайдена швидкість				дорівнює швидкості центру мас системи VC , яка

для замкненої системи частинок є сталою. Це є відображенням того очевидного факту, що після абсолютно непружного зіткнення внутрішній рух системи частинок припинився. Повні механічні енергії системи двох частинок до і після зіткнення є, відповідно,

E	m 2	m 2
	1 1	2 2	(5.156)
	2	2	(5.156)
	2	2

10У лекційному експерименті для демонстрації такого зіткнення використовують дві пластилінові попередньо підігріті кулі, підвішені на довгих нитках, так щоб їх центри знаходились на одній висоті. Потім одну з куль відхиляють від положення рівноваги і відпускають. Після зіткнення кулі злипаються і далі рухаються разом.

200

та

		)2
E	(m1 m2 )(	)2	(m1 1	m2 2 )2	m12 12 m22 22 2m1m2 1 2	.	(5.157)
E						.	(5.157)
	2		2(m1 m2 )		2(m1 m2 )

Втрата (зменшення) повної механічної енергії частинок при абсолютно непружному

зіткненні є


E E E								m1 12 m2 22				m12 12 m22 22 2m1m2 1 2
E E E
										2					2(m1 m2 )
		(m 2 m 2 )(m m ) m2 2												m2 2
		(m 2 m 2 )(m m ) m2 2												m2 2			2m m						2
	1			1	2		2		1	2	1		1		2	2		1		2	1		2
										2(m1 m2 )
		m m 2			m m 2															)2
		m m 2			m m 2					2m m			2		m m (				2	)2
		1		2 1			1 2		2	1	2 1		2		1	2	1		2			.		(5.158)
					2(m1 m2 )										2(m1 m2 )							.		(5.158)
					2(m1 m2 )										2(m1 m2 )
Таким чином, зменшення повної механічної енергії при абсолютно непружному зіткненні

пропорційне квадрату відносної швидкості частинок 1																						2		і величині так званої зведеної маси
цих частинок,
				m1m2
						.																		(5.158)
			m m			.																		(5.158)
				1	2

Наприклад, при лобовому абсолютно непружному зіткненні двох частинок однакової

маси m1 m2 m , що рухаються назустріч одна одній з однаковими за модулем швидкостями

				m2	(2)2
	2	,	втрата повної механічної енергії є E			m 2 , тобто вона дорівнює

1				2	2m

початковій повній механічній енергії системи частинок. Отже, рух частинок припиняється, що знаходиться у повній відповідності з експериментом.

Для випадку абсолютно пружного лобового зіткнення (Рис. 5.22б) виконуються як закон збереження імпульсу так і закон збереження енергії

									,
m		m	2	m		m				(5.159)
1	1	2		1	1		2	2

m 2	m 2	m 2	m 2
1 1	2 2	1 1	2 2	.	(5.160)
2	2	2	2

Оскільки рух обох частинок відбувається вздовж однієї прямої, спроектуємо рівняння

(5.159) на напрям швидкості першої частинки

201

m m			2	m m .
1	1	2		1	1	2	2

Отже, маємо систему двох рівнянь з двома невідомими 1

(5.159) та (5.161) у вигляді

m ( ) m (					2	)
1	1	1	2		2		2
m ( 2		2 ) m		( 2			2 )
1	1	1	2			2	2

(5.161)

та . Перепишемо рівняння

(5.162)

(5.163)

Усі різниці швидкостей та їх квадратів у цих двох рівняннях відмінні від нуля – інакше не було б зіткнення. Це дозволяє поділити рівняння (5.163) на рівняння (5.162):

			2	.	(5.164)
1	1		2	2

Таким чином, задача звелася до системи двох простих лінійних рівнянь (5.162) та (5.164) з

двома невідомими. З рівняння (5.164) знаходимо

						2									(5.165)
2	1			1		2
і після підстановки до рівняння (5.162) отримуємо
		2m2 2 (m1					m2 ) 1		2	m1 1 m2 2				(5.166а)
									2					(5.166а)
1							1			m1 m2
				m1 m2						m1 m2
та
				2	m1 1		m2 2	.	(5.166б)
			2	2				.	(5.166б)
2			2			m1	m2
						m1	m2
Розглянемо важливі частинні випадки.
1. Нехай маси частинок однакові, m m											2	. Тоді маємо	2	та		, тобто при
									1		2	1	2	2	1

абсолютно пружному лобовому ударі частинки однакової маси обмінюються швидкостями. У

цьому можна пересвідчитися, наприклад, спостерігаючи лобове зіткнення більярдної кулі, що рухається, з більярдною кулею, що знаходиться на більярдному столі в стані спокою: куля, що рухалась, зупиняється, натомість куля, що була нерухомою, продовжує рух у тому ж напрямі і з тією ж швидкістю, що й перша куля до зіткнення.

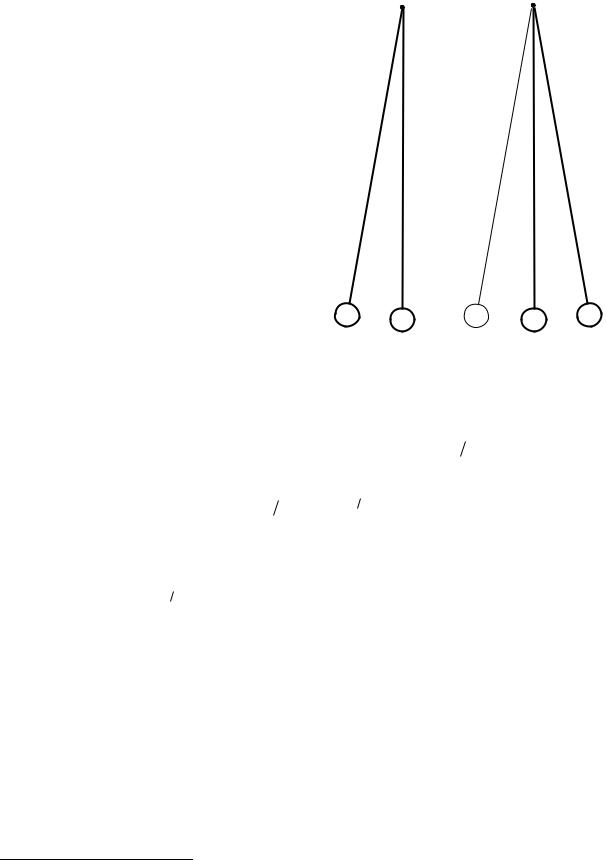
У лекційному демонстраційному досліді дві однакові більярдні кулі підвішують на довгих нитках (Рис. 5.23), потім одну з них відхиляють на невеликий кут та відпускають без надання їй початкової швидкості. Після лобового зіткнення ця куля зупиняється, причому нитка на якій вона висить спрямована строго по вертикалі. Натомість друга куля набуває

202

швидкості і відхиляється на той же самий кут

, на якій було відхилено першу кулю. Потім друга куля, повертаючись до положення рівноваги, стикається з першою кулею,

зупиняється, а перша куля відхиляється практично на той самий кут , після чого процес багаторазово повторюється11. Через декілька періодів стає помітним поступове зменшення максимального кута відхилення аж до повного припинення руху обох куль.

2. Маса однієї частинки набагато більша за масу іншої.

m1	m2	m2
	m2	m1

Рис. 5.23. Демонстраційний дослід з пружного зіткнення куль

Нехай,			наприклад,			легка частинка m1			налітає зі		швидкістю 1		на нерухому важку
частинку m2			( 2	0 ), причому m1 m2 . Тоді у граничному випадку m1									m2 0 маємо
	2			m1 1		2	m1	1					(5.167)
	2					2							(5.167)
1			1	m1	m2	1	m2	1 m1 m2	1	при m1 m2	0	1
				m1	m2		m2	1 m1 m2
та
	2		m1 1		0 ,							(5.168)
	2				0 ,							(5.168)
2		m1 m2			при m1 m2 0
		m1 m2

тобто легка частинка «відбивається» від важкої нерухомої частинки, зберігаючи незмінною величину швидкості, але змінюючи її напрям на протилежний: на це вказує знак « »


у проекції швидкості 1	на напрям швидкості 1	у виразі (5.167). Це відповідає поширеному на

практиці випадку абсолютно пружного зіткнення легкого тіла з масивною нерухомою стінкою,

підлогою тощо. Імпульс легкої частинки m1 змінюється при цьому на протилежний. При цьому

закон збереження імпульсу (5.159) набирає вигляду						. Отже, зміна імпульсу
закон збереження імпульсу (5.159) набирає вигляду	m		m		p	. Отже, зміна імпульсу
	1	1	1	1	2

11Сильне враження справляє перехоплення демонстратором однієї з куль, коли вона досягає найбільшого відхилення: друга куля продовжує висіти нерухомо. Коли демонстратор відпускає затриману відхилену кулю процес поновлюється.

										203
частинки	m1	при		лобовому		зіткненні з	масивною нерухомою перешкодою є

p p p m1 1			m1 1		2m1 1	. Цей імпульс	2m1 1	частинка	m1	відповідно до закону

збереження імпульсу отримує від масивної нерухомої перешкоди (частинки) m2 . Підкреслимо,

що повна механічна енергія системи частинок при цьому залишається незмінною: після

зіткнення частинка m1 має ту саму кінетичну енергію, що й до зіткнення, хоча напрям її

швидкості (імпульсу) є протилежним початковому.

Якщо ж, навпаки, на нерухому легку частинку m2 ( 2 0 )														налітає зі швидкістю 1
важка частинка m1 , причому m1 m2 , то у граничному випадку m2													m1 0
	2			m1 1		m2 2		2		1		2			(5.169)
	2							2				2			(5.169)
1	1				m1	m2		1	1 m2			при m2 m1 0	1	1 1
					m1	m2			1 m2		m1
та
			2		m1 1		m2 2	2 ,							(5.170)
			2					2 ,							(5.170)
2		2			m1		m2	при m2		m1 0	1
					m1		m2
тобто важка частинка m1 продовжує рух з початковою швидкістю 1 , а															легка частинка

m2 «відскакує» від неї з відносною швидкістю 1 , так що її швидкість відносно лабораторної системи відліку стає 2 1 .

Нелобові зіткнення частинок. Діаграми імпульсів. Розглянемо тепер більш складний випадок нелобових зіткнень, коли до або/та після зіткнення обидві частинки рухаються по

траєкторіям, що не лежать на одній прямій.

На

підставі

закону збереження

імпульсу

для замкненої системи двох

частинок (5.152)

можна побудувати векторну діаграму,

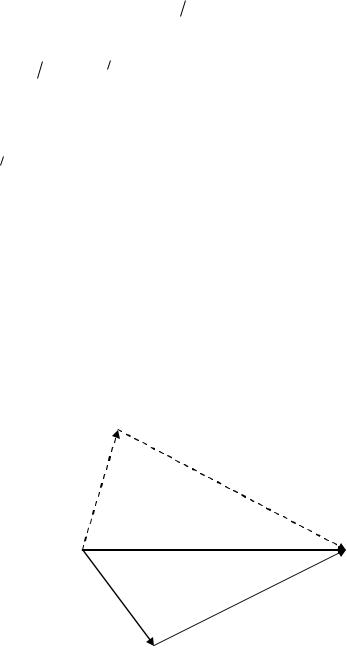
зображену на Рис. 5.29. З неї випливає,

p p

що сума

векторів

імпульсів частинок

після зіткнення p p дорівнює вектору

Рис. 5.29	CD

<<< < Предыдущая 1 2 3 4 5 67 / 87 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.09.2019238.59 Кб156-67.doc
#
19.03.2015142.34 Кб857-61 цпп.doc
#
15.09.201982.43 Кб157.doc
#
18.12.20182.58 Mб5588566.doc
#
09.09.2019330.01 Кб15ballov-92734.rtf
#
19.03.20151.39 Mб85_Zakony zberezhennia.pdf
#
19.03.2015426.22 Кб146 Бюджетний процес в Україні.pdf
#
05.08.201958.46 Кб16,18,36,37.docx
#
19.03.2015172.54 Кб196-9.doc
#
25.11.20193.53 Mб6061.doc
#
19.03.201552.37 Кб661.docx