
5_Zakony zberezhennia
.pdf
144
A12 0 , або «робота проти сили F на деякому шляху», якщо A12 0 . У Прикладі 1 при переміщенні
тіла виконувалась робота проти сили тертя ковзання.
5.2.1. Потенціальна енергія частинки
Відповідно до сучасних уявлень взаємодія між частинками (тілами) здійснюються через силові поля. Якщо до частинки, що знаходиться у деякій області простору, прикладено силу,
яка закономірно змінюється від однієї точки цієї області до іншої, то кажуть, що в цій області простору існує силове поле або поле сили. Серед відомих силових полів можна вказати поле тяжіння Землі, електростатичне поле електричного заряду, магнітне поле постійного магніту тощо. Силове поле є поле вектора сили, тобто належить до векторних полів. Силове поле може
бути |
|
|
|
|
описано шляхом зазначення вектора сили F |
в кожній точці поля: F |
F (r ) або |
||
|
|
|
|
|
F |
F (x, y, z) . |
|
|
|
Якщо сила, прикладена до частинки в кожній точці силового поля, не залежить від часу,
то таке поле називають стаціонарним.
Розглянуті вище приклади показують, що існують як випадки, коли робота сили, при переміщенні тіла залежить від траєкторії (Приклад 1), так і випадки, коли згадана робота не залежить від форми траєкторії, оскільки визначається лише положенням початкової і кінцевої точок траєкторії (Приклад 2).
Дослідимо більш докладно властивості силового поля, в якому робота по переміщенню частинки не залежить від форми траєкторії.
Стаціонарне силове поле, в якому робота сили поля при переміщенні частинки між двома довільними точками поля не залежить від форми траєкторії частинки, що проходить через ці точки, а залежить лише від положення цих точок, називається потенціальним, а сила, прикладена до частинки з боку такого поля, називається
консервативною.
b
1
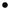 2
2
a
Рис. 5.5. До обчислення роботи
145
Покажемо, що робота консервативних сил при переміщенні частинки по довільній замкненій траєкторії або, як іноді кажуть, по замкненому контуру, дорівнює нулю. На Рис. 5.5
зображено замкнений контур, на якому обрано точки 1 та 2, які поділяють його на дві ділянки
a і b . Тоді роботу A по переміщенню частинки по цьому замкненому контуру, наприклад, із
точки 1 у точку 1 можна подати у вигляді суми робіт на згаданих ділянках контуру a і b :
A Aa |
Ab . |
(5.24) |
12 |
21 |
|
При зміні напряму руху на протилежний робота змінює знак:
Ab |
Ab . |
(5.25) |
21 |
12 |
|
За означенням потенціального поля робота при переміщенні частинки із точки 1 у точку 2
по траєкторіям, одна з яких є ділянка a , а друга – ділянка b замкненого контуру, однакова:
Aa |
Ab . |
|
|
|
(5.26) |
|
12 |
12 |
|
|
|
|
|
Підставляючи до (5.24) спочатку (5.25), а потім (5.26) одержимо |
|
|||||
A Aa |
Ab |
Aa |
Aa |
0 . |
(5.27) |
|
|
12 |
12 |
12 |
12 |
|
|
Легко довести й обернене твердження:
Якщо робота сил деякого поля при переміщенні частинки по довільній замкненій траєкторії дорівнює нулю, то робота цих сил по переміщенню частинки між двома довільними точками поля не залежить від форми траєкторії.
Таким чином, рівність нулю роботи сил поля по переміщенню частинки по довільному замкненому контуру є необхідна і достатня умова незалежності роботи по переміщенню частинки між двома довільними точками поля від форми траєкторії. Отже, ця властивість також може бути покладена в основу означення потенційного поля.
Стаціонарне силове поле, в якому робота сили поля при переміщенні частинки по
замкненому контуру дорівнює нулю, називається потенціальним.
Розглянемо роботу APO по переміщенню частинки з довільної точки P потенціального поля в деяку фіксовану точку O . Ця робота залежить лише від положення точки P , яке можна
характеризувати її радіус-вектором rP або її координатами. Отже, робота APO є функція

радіус-вектора rP
записати
U (rP ) APO
або координат точки P . Позначимо цю функцію як
O
Fdr ,
P
де інтеграл береться вздовж ділянки траєкторії, обмеженої точками
146
U (rP ) . Тоді можна
(5.28)
P та O . Величина
U (rP ) має розмірність енергії. Її називають потенціальною енергією частинки в даному
потенціальному полі. Із способу введення функції U (rP ) видно, що її значення залежать від
вибору точки O . Покажемо, що за допомогою функції U (rP ) можна знайти роботу по
переміщенню частинки з точки поля 1 у точку поля 2 (Рис. 5.6). Оберемо траєкторію, що
з’єднує точки 1 та 2 і проходить через точку O . Тоді роботу A12 по переміщенню частинки з
точки поля 1 у точку поля 2 |
можна подати у вигляді суми роботи A10 по переміщенню |
частинки з точки 1 у точку O та |
роботи A02 по переміщенню частинки з точки O у точку 2: |
|
|
|
|
A12 A10 A02 A10 A20 U (r1 ) U (r2 ) , |
|||
тобто |
|
|
|
A12 U1 U2 |
або A12 (U2 |
U1 ) , |
(5.30) |
|
|
|
|
де позначено U1 U (r1 ) , U 2 |
U (r2 ) . |
||
Отже, робота по переміщенню частинки в |
|||
потенціальному |
полі може |
бути |
подана як приріст |
потенціальної енергії U U 2 U1 , взятий зі знаком «мінус»: |
|||
2 |
|
|
|
|
A12 Fdr |
U , |
(5.31) |
||
1 |
|
|
|
|
(5.29)
O
1
2
Рис. 5.6. До обчислення роботи
по переміщенню частинки в
|
|
а на елементарному переміщенні dr |
|
|
(5.32) |
A Fdr dU . |
|
Підкреслимо, що хоча значення функції U1 |
та U 2 і залежать від вибору точки O , їх |
різниця, що дорівнює роботі по переміщенню частинки з точки 1 в точку 2 не залежить від
147
вибору точки O . Іншими словами, частинці, що знаходиться в точці O , може бути приписане довільне значення потенціальної енергії.
До класу потенціальних належать так звані центральні силові поля, в яких силу, що діє на частинку, можна подати загальною формулою
|
|
|
|
|
|
|
r |
|
|
||
F |
(r ) |
f (r) |
|
, |
(5.33) |
r |
де f (r) – деяка скалярна функція, що залежить лише від відстані r |
|
|
|
, до деякої точки, |
|||
|
|
||||||
|
r |
|
|||||
що називається силовим центром, а |
r |
– одиничний вектор співнапрямлений з радіус-вектором |
|||||
r |
|||||||
|
|
|
|
|
|
||
r . Модуль сили в такому полі залежить лише від відстані r до силового центру (до центру поля), тобто має однакову величину в усіх точках, що лежать на сфері радіуса r , а лінія дії сили завжди проходить через центр поля.
Робота сил центрального поля по переміщенню частинки з однієї точки поля в іншу є
r2 |
|
A12 f (r)dr . |
(5.34) |
r1 |
|
Порівнюючи (5.33) з формулами сил, наведеними в Розділі 3, можна побачити, що до класу центральних належать сила всесвітнього тяжіння, кулонівська сила, квазіпружна сила. У
цьому легко переконатися, наприклад, для гравітаційного поля, розглядаючи одну з частинок як центр силового поля і помістивши в нього початок відліку.
Із викладеного вище випливає послідовність дій по відшуканню функції потенціальної енергії потенціального силового поля за відомою формулою сили, що діє на частинку в цьому полі: спочатку необхідно обчислити роботу сил поля з переміщення частинки між двома довільними точками поля, а потім подати її у вигляді приросту деякої функції положення точки
(функції радіус-вектора або координат), взятого зі знаком мінус. Ця функція і буде функцією потенціальної енергії цього поля.
Приклад. Обчислення потенціальної енергії частинки в полі точкової маси або електричного
заряду.
Силу кулонівської або гравітаційної взаємодії між двома частинками можна подати у загальному
вигляді
148
|
|
|
|
|
|
Gm1m2 |
для гравітаційного поля |
|
|
|
|
r |
|
|
|||||
F |
|
|
|
|
, |
де |
|
|
(5.34) |
r 2 |
|
r |
kq1q2 |
для кулонівського поля |
|||||
|
|
|
|
|
|
||||
Робота по переміщенню частинки в такому силовому полі вже була обчислена вище (див. формулу
(5.23)). Її можна подати так
|
|
1 |
|
1 |
|
|
|
|
|
|
|
A12 |
|
|
|
|
|
|
|
|
|
|
[U (r2 ) U (r1)] , |
|
r |
|
r |
||||||||
|
r |
|
|
r |
|
|
|
||||
|
|
2 |
|
1 |
|
|
2 |
|
1 |
|
|
звідки знаходимо вираз для потенціальної енергії частинки в такому полі
U (r) |
. |
(5.36) |
|
r |
|
Відповідно, для гравітаційного поля маємо
U (r) G |
m1m2 |
, |
(5.37) |
|||
r |
||||||
|
|
|
|
|||
а для кулонівського |
|
|
||||
U (r) k |
q1q2 |
. |
|
(5.38) |
||
|
|
|||||
|
|
r |
|
|
||
(5.35)
U(r)
Кулонівське
відштовхування
O
r
 Гравітаційне та кулонівське
Гравітаційне та кулонівське
Рис. 5.7. Залежність потенціальної
Зауважимо, що скалярне поле потенціальної енергії, що існує навколо точкової маси або точкового
заряду (5.37, 5.38), має центральну симетрію, тобто потенціальна енергія залежить лише від модуля відстані до силового центру, як і має бути для центрального поля. Відповідні графіки подано на Рис. 5.7.
Еквіпотенціальні поверхні. Геометричне місце точок, в яких потенціальна енергія частинки однакова, утворює в просторі поверхню, яку називають поверхнею однакового потенціалу або еквіпотенціальною поверхнею (від латинського aequus – однаковий, рівний).
Рівняння еквіпотенціальної поверхні U (x, y, z) const . Цілком очевидно, що робота по
переміщенню частинки по еквіпотенціальній поверхні дорівнює нулю. Уявлення про
форму еквіпотенціальних |
поверхонь дають |
їх |
перерізи, |
|
що зображають сімейство |
|
еквіпотенціальних поверхонь для різних значень |
U , які, |
як |
правило, |
відрізняються на |
||
постійну величину. Для центральних полів |
еквіпотенціальні |
поверхні |
являють собою |
|||
концентричні сфери. |
|
|
|
|
|
|
149
5.2.2. Зв’язок між потенціальною енергією та силою
Знайдемо зв’язок між функцією потенціальної енергії частинки в деякому силовому полі та консервативною силою, що прикладена до частинки з боку цього поля. Скористаємося
виразом (5.32), який |
зв’язує елементарний |
приріст |
dU потенціальної енергії U (x, y, z) з |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
елементарною роботою A консервативної сили F (x, y, z) на елементарному переміщенні dr |
||||||||||||||||||||||||
поблизу точки поля з координатами x, y, z , і запишемо |
|
|
|
|
|
|
||||||||||||||||||
|
|
dU . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.39) |
||||
|
Fdr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Елементарний приріст функції 3-х змінних x, y, z |
U (x, y, z) з точністю до нескінченно |
||||||||||||||||||||||
малих першого порядку можна подати її повним диференціалом |
|
|
|
|
||||||||||||||||||||
|
dU U dx U dy U dz , |
|
|
|
|
|
|
|
|
|
|
|
(5.40) |
|||||||||||
|
|
|
x |
y |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де dx, dy, dz – |
нескінченно |
малі |
незалежні |
один від одного прирости |
координат, |
а |
|||||||||||||||||
U |
U |
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U (x, y, z) обчислені в |
|
|
|
|
|
x , |
y |
, |
z – |
так звані частинні похідні функції |
точці |
поля |
з |
|||||||||||||||||
координатами x, y, z . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Наприклад, |
частинну похідну |
|
U |
функції U (x, y, z) |
в точці поля з координатами |
x , y , z |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
обчислюють |
так: |
беруть похідну |
|
|
d |
|
U (x, y, z) , вважаючи |
дві інші змінні, |
x, y , |
сталими |
||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|||
величинами, і в отриманий вираз підставляють x x0 , y y0 , |
z z0 . |
|
|
|
|
|||||||||||||||||||
|
Скалярний добуток у лівій частині (5.40) є |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Fxdx |
Fy dy Fz dz . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Fdr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.41) |
|||||||
|
Отже після підстановки (5.40) та (5.41) у (5.39) одержимо рівність |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
U |
dx |
U |
dy |
|
U |
|
|
|
|
(5.42) |
||||||||
|
F dx F dy F dz |
|
|
|
|
|
|
dz . |
|
|
||||||||||||||
|
x |
|
y |
z |
|
x |
|
|
|
|
|
y |
|
|
z |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
З порівняння коефіцієнтів при однакових приростах незалежних змінних у лівій та правій
частинах цієї рівності дістанемо зв’язок між компонентами вектора сили F , прикладеної до частинки з боку потенціального поля в точці простору з координатами x, y, z , та частинними

150
похідними від функції потенціальної енергії U (x, y, z) частинки, обчисленими в цій точці:
F U |
, F |
y |
U |
, F U . |
(5.43) |
||
x |
x |
|
y |
z |
z |
|
|
|
|
|
|
|
|||
Сам вектор сили F є
|
|
U |
|
U |
|
U |
, |
(5.44) |
|
F |
|
i |
j |
|
k |
||||
|
|
x |
|
y |
|
z |
|
|
|
|
|
|
|
|
|
|
|||
де i , j, k – орти декартової системи координат. Рівність (5.44) встановлює відповідність
між множиною значень скалярної величини потенціальної енергії частинки в околі точки з
координатами x, y, z , в деякому потенціальному полі U (x, y, z) і значенням векторної
|
|
|
|
величини сили F (x, y, z) , що прикладена до частинки в цій точці простору, |
тобто встановлює |
||
зв’язок між скалярним полем U (x, y, z) і векторним полем |
|
|
|
F(x, y, z) . |
|
||
Рівність (5.44) часто записують більш компактно у вигляді |
|
||
|
|
|
|
F |
U , |
|
(5.45) |
де використано позначення так званого оператора2 набла (значок читається
«набла»)
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
||||
|
|
x |
|
|
y |
|
|
|
|
||
|
|
|
|
|
j |
|
|
k |
(5.46) |
|
||||
|
|
z |
. |
|
|
|
|
|
Дія оператора , який формально можна розглядати як вектор, компонентами якого є оператори частинних похідних за декартовими координатами, на скалярну функцію,
формально можна розглядати як множення цього вектора на скаляра. У цьому і лише в цьому
випадку його називають оператором градієнта і часто позначають як grad , тобто запис
2 Термін «оператор» означає, взагалі, дещо, що виконує якусь операцію у широкому розумінні слова, наприклад,
операцію встановлення відповідності між елементами двох множин, і є синонімом термінів «відображення», «функція». Оператор можна розглядати як алгоритм, послідовність математичних операцій, які дають можливість
встановити бажану відповідність між елементами двох множин. У нашому випадку дія оператора зводиться до такої послідовності операцій: 1) знаходження частинних похідних від U (x, y, z) ; 2) множення кожної з них на відповідний орт; 3) сумування цих добутків і, нарешті, 4) множення отриманого таким чином вектора на -1.
151
U є тотожним запису gradU . Отже, рівність (5.45) можна також записати у вигляді
|
gradU . |
|
F |
(5.47) |
Результатом дії оператора градієнта на поле деякої скалярної величини є вектор, який називають градієнтом цієї величини. Можна показати, що градієнт вказує напрям
найшвидшого зростання величини скалярного поля.
Отже, до частинки, що знаходиться в потенціальному полі, з боку цього поля
прикладена сила, що дорівнює градієнту потенціальної енергії частинки в точці її знаходження, взятому зі знаком мінус.
5.2.3. Повна механічна енергія частинки
Сили, прикладені до частинки, в загальному випадку завжди можна розділити на консервативні або потенціальні та неконсервативні або сторонні. Відповідно до (5.18) сумарна робота цих сил змінює кінетичну енергію частинки:
dT Aконс Aстор . |
(5.46) |
|||
Оскільки, Aконс dU , то |
|
|||
dT dU Aстор |
(5.47) |
|||
або |
|
|
|
|
d (T U ) Aстор . |
(5.48) |
|||
Величина |
E T U , сума кінетичної та потенціальної енергії |
частинки, називається |
||
повною механічною енергією частинки, |
|
|||
|
m 2 |
|
|
|
E |
|
U (r ) . |
(5.49) |
|
2 |
||||
|
|
|
||
З означення (5.49) видно, що повна механічна енергія частинки є функцією механічного стану частинки.
Умови зміни та збереження повної механічної енергії частинки. Відповідно до рівняння (5.48) приріст повної механічної енергії частинки на елементарному переміщенні дорівнює елементарній сумарній роботі всіх сторонніх сил,
dE Aстор , |
(5.50) |
152
а на скінченному переміщенні
E |
2 |
E |
Aстор , |
(5.51) |
|
1 |
12 |
|
де A12стор є сумарна робота всіх сторонніх сил на шляху між точкою 1 і точкою 2.
Оскільки
Aстор N сторdt , |
(5.52) |
то повна механічна енергія частинки E змінюється, |
якщо сумарна потужність сторонніх сил |
N стор , прикладених до частинки в кожен момент часу відмінна від нуля. Якщо N стор 0 , то |
|
повна механічна енергія частинки E зростає, а якщо |
N стор 0 , то зменшується. Відповідно, |
приріст повної механічної енергії частинки на деякому шляху дорівнює алгебраїчній сумі робіт
Aстор всіх сторонніх сил, що діють на частинку на цьому шляху: якщо Aстор 0 , то повна механічна енергія на цьому шляху зростає, а якщо Aстор 0 , то зменшується.
З рівнянь (5.50) та (5.52) випливає умова збереження повної механічної енергії частинки:
повна механічна енергія частинки зберігається, якщо сумарна потужність або робота всіх
сторонніх сил, що прикладені до частинки, дорівнює нулю.
Якщо сторонні сили взагалі відсутні, то їх потужність у правій частині рівняння (5.52)
завжди дорівнює нулю. Тоді справедливий закон збереження повної механічної енергії частинки:
Повна механічна енергія частинки, на яку не діють сторонні сили, зберігається,
тобто
T U const |
|
m 2 |
|
|
|
або |
|
U (r ) const . |
(5.53) |
||
2 |
|||||
|
|
|
|
5.2.4. Одновимірний рух частинки в потенціальному полі
У демонстраційному досліді частинка (невелика сталева кулька) рухається по плоскій
траєкторії, що лежить у вертикальній площині і проходить на різній висоті h над поверхнею демонстраційного стола (котиться вздовж направляючої, виготовленої з кутника) (Рис. 5.8).
Потенціальна енергія кульки в однорідному полі сили тяжіння є U (x) mgh(x) , де h(x)
висота кульки над поверхнею стола в точці з координатою x , яка відлічується вздовж поверхні
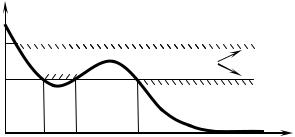
153
стола від початку направляючої, де її висота максимальна На направляючій є неглибокий мінімум на відстані порядку 1 м від початку (на Рис. 5.8 обрано різний масштаб по горизонталі
та по вертикалі: hmax |
0,4 м, xmax 4 м). |
U(x) |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Повна механічна енергія кульки є |
|
|
|
|
|
|
|||
E T (x) U (x) . |
|
|
|
E1 |
|
|
|
|
|
|
(5.54) |
|
фінітний |
інфінітний |
|
||||
|
|
E2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
Якщо |
помістити |
кульку |
на |
|
|
|
|
|
|
направляючій на деякій висоті h1 більшій |
0 |
x1 |
x2 |
x3 |
x |
||||
за висоту максимуму між точками x2 |
та |
Рис. 5.8. До одновимірного руху частинки. |
|||||||
|
|
|
|
|
|||||
x3 і відпустити без надання їй початкової швидкості, то її повна механічна енергія E1 |
буде |
||||||||
повністю |
визначатися |
її |
початковою |
потенціальною |
енергією |
U mgh1 . Під |
дією |
||
консервативної сили тяжіння кулька почне рухатись і її кінетична енергія буде зростати за рахунок роботи цієї сили, а потенціальна енергія спадати. Оскільки опір руху кульки при її коченні є дуже малий (так званий коефіцієнт тертя кочення набагато менший за коефіцієнт тертя ковзання), а опір повітря при малих швидкостях також незначний, то на невеликих
проміжках часу можна вважати, що повна механічна енергія кульки зберігається, E const .
Тому після проходження мінімуму між точками x1 та x2 потенціальна енергія частинки
починає зростати, а кінетична зменшуватись і, відповідно, зменшуватись швидкість. Після
проходження максимуму між точками x2 та x3 потенціальна енергія частинки знову
зменшується, а кінетична зростає, оскільки повна енергія частинки залишається сталою. Рух
кульки можливий лише на тих ділянках, де кінетична енергія додатна, тобто при E U (x) ,
оскільки швидкість має бути дійсною величиною. Ділянки, де E U (x) є недосяжними для
механічного руху. У зв’язку з цим, одновимірний рух може бути інфінітним, коли частинка прямує на нескінченність (у нашому випадку кулька може котитися по поверхні стола у напрямку необмеженого збільшення x ), або фінітним, коли частинка не виходить за межі
деякої ділянки між x1 та x2 , де виконується умова E U (x) . Для ходу
потенціальної енергії U (x) , зображеного на Рис. 5.8, фінітний рух може мати місце поблизу
