
898
.pdf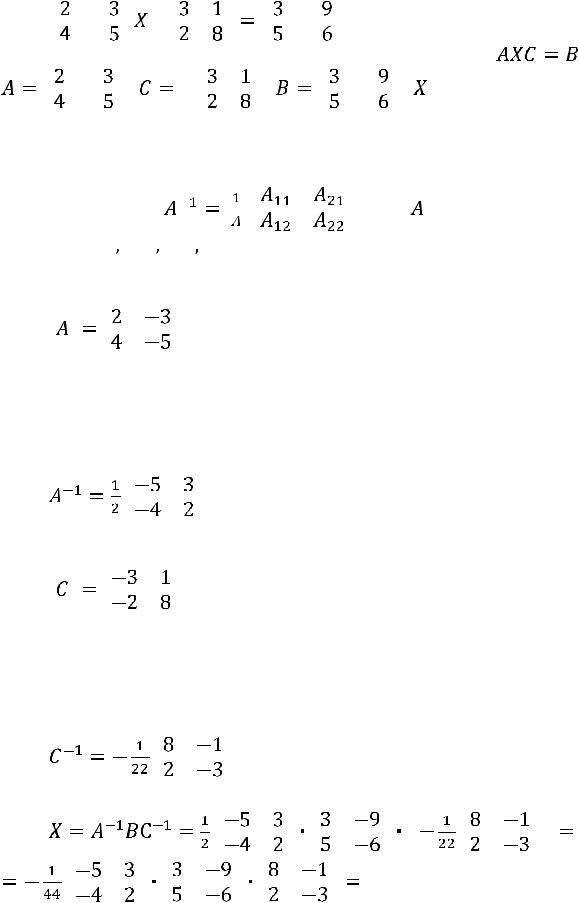
Пример. Решить матричное уравнение |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
Запишем данное уравнение в виде |
, где |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
, |
, |
|
|
|
, – матрица неизвест- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ных. Решением этого уравнения является матрица
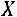

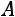

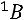


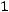 .
.
Найдѐм матрицу 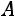

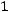 . Используем формулу нахождения об-
. Используем формулу нахождения об-
ратной матрицы: |
|
|
|
, где |
– определитель мат- |
|
|||||
|
|
|
рицы 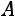 ;
; 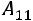
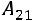
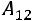
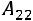 – алгебраические дополнения элементов матрицы
– алгебраические дополнения элементов матрицы 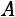 .
.
Найдѐм определитель матрицы 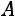 :
:


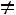
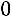 .
.
Так как матрица 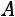 невырожденная, то для неѐ существует обратная.
невырожденная, то для неѐ существует обратная.
Найдѐм алгебраические дополнения элементов матрицы  :
: 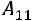


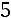 ,
, 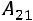

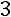 ,
, 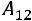


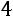 ,
, 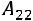

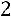 .
.
Матрица, обратная для 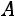 имеет вид:
имеет вид:
.
Найдѐм матрицу 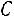

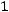 .
.
Найдѐм определитель матрицы 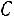 :
:


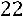
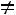
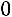 .
.
Так как матрица 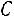 невырожденная, то для неѐ существует обратная.
невырожденная, то для неѐ существует обратная.
Найдѐм алгебраические дополнения элементов матрицы 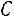 :
: 

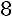 ,
, 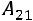


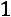 ,
, 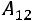

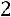 ,
, 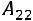


 .
.
Матрица, обратная для 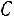 имеет вид:
имеет вид:
.
Найдѐм матрицу неизвестных:
71

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Ответ: |
. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
Задание 13. Решить матричное уравнение. |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
72 |
|
||||||||||||||||||||||

11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
12. |
. |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
13. |
. |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
14. |
. |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
]15. |
. |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
16. |
. |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
17. |
. |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
18. |
. |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
19. |
. |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
20. |
. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
21. |
. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
22. |
. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
23. |
. |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
24. |
. |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
73 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||

25. |
|
|
|
|
|
|
|
. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
26. |
. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
27. |
. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
28. |
. |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
29. |
. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
30. |
. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
31. |
. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
32. |
. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
33. |
. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
34. |
. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
35. |
. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
36. |
. |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
74

Модель Леонтьева многоотраслевой экономики Справочный материал.
Моделью Леонтьева многоотраслевой экономики или уравнением линейного межотраслевого баланса называется матричное
уравнение |
, |
где |
– вектор валового выпуска, |
||||
|
|
– матрица прямых затрат, |
– вектор конечного |
||||
продукта; |
– общий (валовой) |
объѐм продукции i-й отрасли; |
|||||
|
|
, |
– объѐм продукции i-й отрасли, потребляемый j-й от- |
||||
|
|||||||
раслью в процессе производства; |
– объѐм конечного продукта i-й |
||||||
отрасли для |
непроизводственного |
потребления; |
. |
||||
Все величины имеют стоимостное выражение. |
|
|
|||||
Модель Леонтьева называется продуктивной, если продуктив- |
|||||||
на матрица |
. Матрица |
с неотрицательными элементами называ- |
|||||
ется продуктивной, если для любого вектора |
с неотрицательными |
||||||
элементами существует вектор 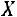 с неотрицательными элементами.
с неотрицательными элементами.
Критерий продуктивности матрицы 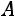 . Матрица
. Матрица 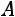 с неотри-
с неотри-
цательными элементами продуктивна, если максимум сумм элементов еѐ столбцов не превосходит единицы, причѐм хотя бы для одного из столбцов сумма элементов строго меньше единицы, то есть 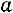

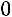 ,
, 
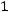
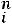

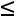
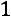 и существует такой номер j, что
и существует такой номер j, что
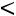
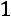 .
.
Основная задача межотраслевого баланса состоит в нахождении такого вектора 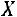 , который при известной матрице
, который при известной матрице 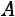 обеспечивает заданный вектор
обеспечивает заданный вектор  . Вектор
. Вектор 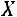 можно найти методом обратной
можно найти методом обратной
матрицы по формуле: |
|
|
|
, где |
– единичная матрица. |
|
|
|
|||
|
|||||
Пример. Дана матрица прямых затрат |
. Найти |
||||
вектор валовой продукции 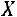 , обеспечивающий выпуск конечной продукции
, обеспечивающий выпуск конечной продукции 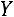
 .
.
Решение.
Проверим критерий продуктивности.
1)Элементы матрицы 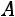 неотрицательны.
неотрицательны.
2)Сумма элементов первого столбца:
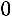
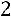

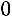
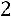

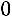

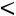
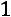 , 3) сумма элементов второго столбца:
, 3) сумма элементов второго столбца:
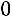
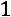


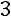

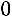
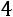
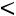
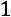 .
.
75

Критерий продуктивности выполняется, поэтому для вектора  можно найти вектор
можно найти вектор 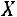 .
.
Найдѐм матрицу 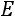

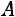 :
:
.
Найдѐм матрицу, обратную для 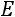

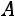 : 1) Вычислим определитель:
: 1) Вычислим определитель:

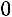
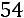 .
.
2) Вычислим алгебраические дополнения:
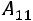

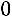
 ,
, 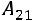

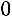
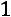 ,
, 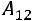

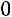
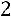 ,
, 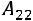

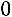
 . 3) Запишем обратную матрицу:
. 3) Запишем обратную матрицу:
.
Тогда вектор валовой продукции:
.
Ответ: общий объѐм выпуска продукции первой отрасли должен составлять 630 ден. ед., второй – 490 ден. ед.
Задание 14. Дана матрица прямых затрат 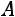 . Найти вектор валовой продукции Х, обеспечивающий выпуск конечной продукции
. Найти вектор валовой продукции Х, обеспечивающий выпуск конечной продукции
 .
.
1. |
, |
. |
2. |
, |
. |
3. |
, |
. |
4. |
, |
. |
5. |
, |
. |
76

6. |
, |
. |
7. |
, |
. |
8. |
, |
. |
9. |
, |
. |
10. |
, |
. |
11. |
, |
. |
12. |
, |
. |
13. |
, |
. |
14. |
, |
. |
15. |
, |
. |
16. |
, |
. |
17. |
, |
. |
18. |
, |
. |
19. |
, |
. |
77

20. |
, |
. |
21. |
, |
. |
22. |
, |
. |
23. |
, |
. |
24. |
, |
. |
25. |
, |
. |
26. |
, |
. |
27. |
, |
. |
28. |
, |
. |
29. |
, |
. |
30. |
, |
. |
31. |
, |
. |
32. |
, |
. |
78

33. |
, |
. |
34. |
, |
. |
35. |
, |
. |
36. |
, |
. |
Ранг матрицы Справочный материал.
Рангом матрицы 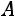 называется максимальное число линейно независимых столбцов этой матрицы. Обозначение:
называется максимальное число линейно независимых столбцов этой матрицы. Обозначение:
.
В курсе высшей алгебры доказывается, что ранг матрицы равен наибольшему порядку миноров этой матрицы, отличных от нуля.
Пусть дана матрица, содержащая m строк и n столбцов. Выделим в ней произвольным образом к строк и к столбцов. Элементы, которые находятся на пересечении выделенных строк и столбцов, образуют матрицу к-ого порядка, определитель которой называется минором к-ого порядка матрицы 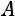 .
.
Свойства ранга матрицы.
1. Если матрица 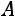 имеет размер
имеет размер 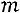

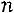 , то:
, то:
|
|
. |
|
2. |
тогда и только тогда, когда все элементы матрицы |
||
равны нулю. |
|
|
|
3. Если |
– квадратная матрица порядка n, то |
тогда и |
|
только тогда, когда |
. |
|
|
С помощью элементарных преобразований матрицу можно привести к ступенчатому виду (элементы, расположенные ниже главной диагонали, равны нулю):
,
где 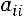
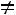
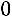
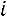

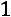
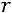
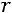
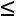
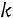 .
.
79
Элементарные преобразования матрицы.
1.Отбрасывание нулевой строки (столбца) матрицы.
2.Умножение всех элементов строки (столбца) матрицы на число, не равное 0.
3.Изменение порядка строк (столбцов) матрицы.
4.Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца).
5.Транспонирование матрицы.
Теорема. При элементарных преобразованиях ранг матрицы не меняется.
Ранг ступенчатой матрицы равен r, то есть количеству ненулевых строк.
Ранг матрицы можно найти двумя способами.
Первый способ (с помощью окаймляющих миноров). Сначала нужно найти отличный от нуля минор первого порядка. Если такого нет, то ранг матрицы равен 0. Затем найти отличный от нуля минор второго порядка, содержащий найденный выше отличный от нуля минор первого порядка. Если такого нет, то ранг матрицы равен 1. Далее найти отличный от нуля минор третьего порядка, содержащий найденный выше отличный от нуля минор второго порядка. Если такого нет, то ранг матрицы равен 2 и т. д.
Второй способ (с помощью элементарных преобразований). С
помощью элементарных преобразований матрицу привести к ступенчатому виду. Количество ненулевых строк полученной матрицы равно рангу матрицы.
Пример. Найти ранг матрицы
.
Решение.
Первый способ. Найдѐм отличный от нуля минор первого порядка. Например, вычеркнем в матрице первую строку и первый столбец. На пересечении находится число 2, которое и является одним из миноров первого порядка: 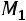

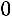 .
.
Затем найдѐм отличный от нуля минор второго порядка, содержащий минор 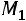

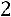 . Для этого вычеркнем, например, первую и вторую строки и первый и второй столбцы. На пересечении полу-
. Для этого вычеркнем, например, первую и вторую строки и первый и второй столбцы. На пересечении полу-
80
