
898
.pdf

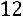

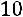

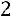 ;
;


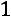 ;
;



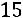


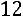 ;
;

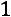 ;
;
Составим обратную матрицу:
.
Второй способ. Запишем матрицу 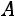
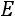 :
:
.
С помощью элементарных преобразований приведѐм матрицу 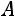
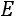 к ступенчатому виду.
к ступенчатому виду.
1. Поменяем местами первую и вторую строки:
.
2. Ко второй строке прибавим первую, умноженную на 
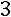 , к третьей строке прибавим первую, умноженную на
, к третьей строке прибавим первую, умноженную на 
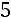 :
:
.
3. Вторую строку умножим на 12, третью строку умножим на
:
.
4. К третьей строке прибавим вторую:
41

.
5. Вторую строку разделим на 
 :
:
.
Таким образом, матрица 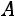
 приведена к ступенчатому виду. Далее матрицу
приведена к ступенчатому виду. Далее матрицу 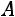
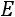 приведѐм к виду
приведѐм к виду 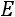
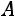

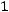 .
.
6. Разделим вторую строку на 7, третью строку разделим на
:
.
7. Ко второй строке прибавим третью, умноженную на |
|
|
|
: |
|
|
.
8. Прибавим к первой строке вторую, умноженную на 
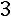 :
:
.
9. Прибавим к первой строке третью, умноженную на 
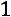 :
:
.
Таким образом, |
|
|
|
. |
|
||||
|
|
Сделаем проверку. Для этого умножим обратную матрицу 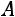

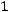 на данную матрицу
на данную матрицу 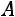 , используя операции умножения матриц и умножения матрицы на число:
, используя операции умножения матриц и умножения матрицы на число:

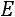 .
.
42

Так как в результате получилась единичная матрица, то обратная матрица найдена верно.
Ответ: |
|
|
|
|
|
. |
|
||||||
|
|
|||||
|
|
|
|
|
|
|
|
Задание 8. Дана матрица |
. Найти для неѐ обратную |
|
|
. |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
. |
|
2. |
|
|
|
|
|
. |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
5. |
|
|
|
|
|
|
|
. |
6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
9. |
|
|
|
|
|
|
|
|
|
|
|
10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
11. |
|
|
. |
12. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
13. |
|
|
|
|
. |
14. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
15. |
|
|
|
. |
16. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
43

17. |
|
|
|
|
|
|
|
. |
18. |
|
|
|
|
|
. |
||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
19. |
|
|
|
|
|
|
|
. |
20. |
|
|
. |
|||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
21. |
|
|
|
|
|
. |
22. |
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|||||||||||||
23. |
|
|
|
|
|
|
|
24. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
. |
|
|
|
|
. |
|||||||
|
|
|
|
|
|
|
|
||||||||||||
25. |
|
|
|
|
. |
26. |
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
. |
|||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
27. |
|
|
|
|
|
. |
28. |
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
29. |
|
|
|
|
|
. |
30. |
|
|
|
|
. |
|||||||
|
|
|
|
|
|
|
|||||||||||||
31. |
|
|
|
|
|
32. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
. |
|
|
|
|
. |
|||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
33. |
|
|
|
|
. |
|
34. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
. |
||||||||||
|
|
|
|
|
|
|
|||||||||||||
35. |
|
|
|
|
. |
36. |
|
|
|
|
|||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
. |
||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
44
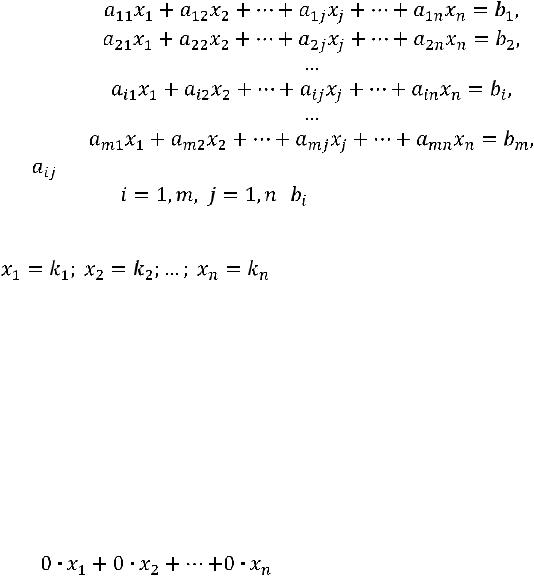
ТЕМА 2. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Справочный материал.
Система из m линейных уравнений с n неизвестными имеет
вид:
где |
– произвольные числа, называемые коэффициентами при |
||
неизвестных, |
; |
− произвольные числа, называе- |
|
мые свободными элементами. |
|
||
|
Решением системы |
называется такая совокупность n чисел |
|
|
|
, |
при подстановке которых каждое |
уравнение системы обращается в верное равенство.
Система уравнений называется совместной, если она имеет хотя бы одно решение; если система не имеет решений, то она называется несовместной. Совместная система называется определѐнной если она имеет единственное решение, и неопределѐнной, если имеет бесконечное множество решений. Системы уравнений называются эквивалентными, если они имеют одно и то же множество решений.
Элементарные преобразования, приводящие к эквивалентной системе:
1. вычѐркивание уравнения вида:

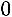 (нулевой строки);
(нулевой строки);
2.перестановка уравнений или слагаемых в уравнении;
3.прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженного на любое действительное число.
Система уравнений в матричной форме имеет вид: 

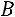 ,
,
где
45

– матрица системы, |
– мат- |
рица неизвестных, |
– матрица свободных элементов. |
Расширенной матрицей системы называется матрица вида:
.
Методы решения систем линейных алгебраических уравнений
Справочный материал.
1. Правило Крамера. По правилу Крамера можно решать системы, когда число уравнений равно числу неизвестных.
Теорема. Пусть 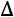 − определитель матрицы системы, а
− определитель матрицы системы, а 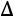 − определитель, полученный из
− определитель, полученный из 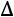 заменой j-ого столбца столбцом свободных элементов. Тогда, если
заменой j-ого столбца столбцом свободных элементов. Тогда, если 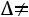
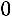 , то система имеет един-
, то система имеет един-
ственное решение, определяемое по формулам 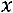

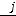 ,
, 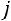

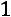
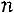 .
.
2.Метод обратной матрицы. Методом обратной матрицы можно решать системы, когда число уравнений равно числу неизвестных. Если матрица системы невырожденная, то матрицу неизвестных находят по формуле 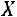

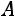

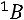 .
.
3.Метод Гаусса. Методом Гаусса можно решать системы с любым числом уравнений и неизвестных. Этот метод основан на приведении расширенной матрицы системы с помощью элементарных преобразований (приводящих к эквивалентной системе) к ступенчатому виду с последующим постепенным нахождением неизвестных, начиная с последних неизвестных.
Пример. Решить систему линейных алгебраических уравнений по правилу Крамера, методом обратной матрицы и методом Гаусса:
46
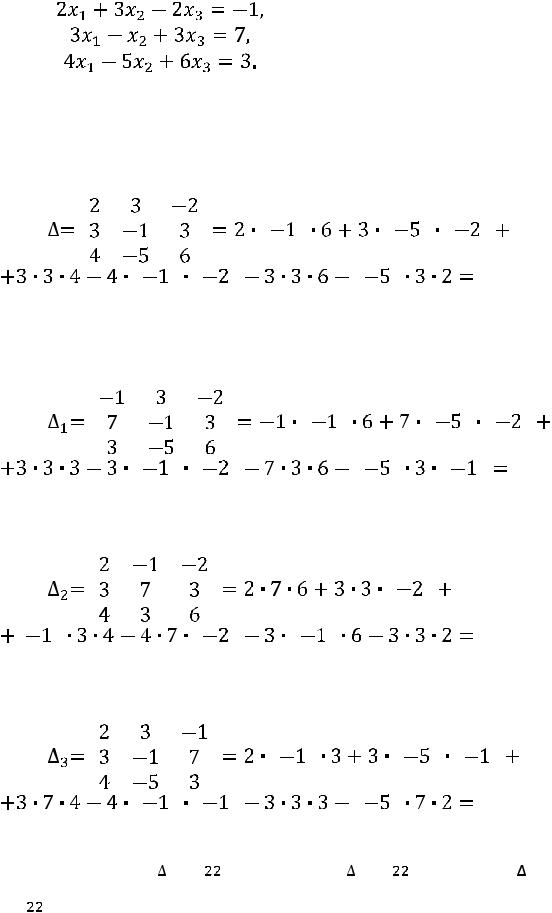
Решение.
1. Правило Крамера.
Так как число уравнений равно числу неизвестных и определитель матрицы системы (определитель, составленный из коэффициентов при неизвестных) отличен от нуля:


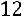

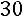

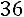

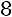

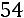

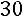

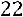
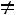
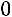 ,
,
то правило Крамера применимо.
Вычислим определитель 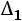 , который получается из
, который получается из  заменой первого столбца столбцом свободных элементов:
заменой первого столбца столбцом свободных элементов:



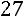

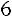

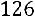

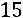


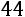 .
.
Вычислим определитель 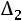 , который получается из
, который получается из 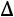 заменой второго столбца столбцом свободных элементов:
заменой второго столбца столбцом свободных элементов:





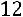

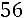

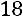

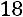

 .
.
Вычислим определитель 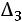 , который получается из
, который получается из 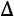 заменой третьего столбца столбцом свободных элементов:
заменой третьего столбца столбцом свободных элементов:


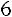

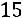

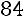

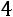

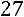

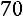

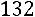 .
.
Тогда 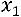

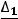

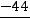


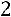 ,
, 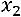

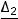

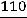

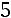 ,
, 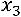




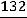

 .
.
Ответ: 
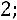

 .
.
47
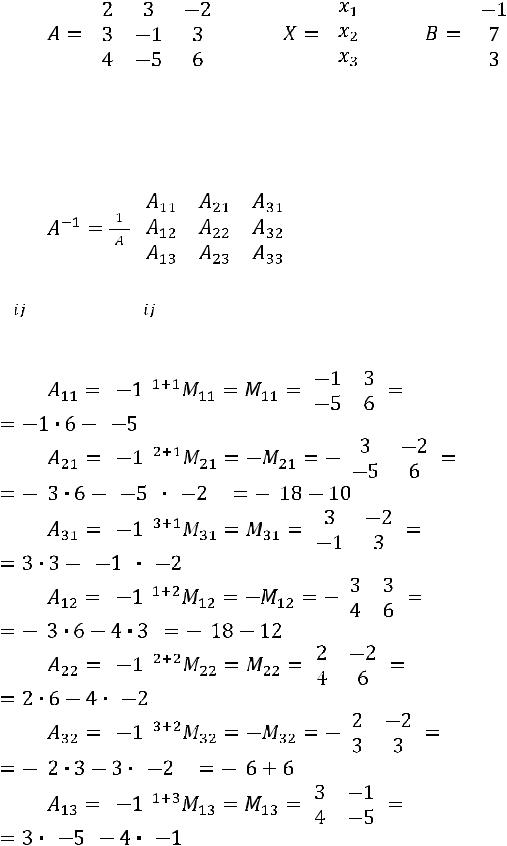
2. Метод обратной матрицы.
Составим матрицу системы 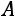 , матрицу неизвестных
, матрицу неизвестных 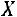 и матрицу свободных элементов
и матрицу свободных элементов 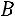 :
:
, |
, |
. |
Так как число уравнений равно числу неизвестных и определитель матрицы системы 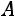

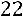
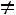
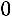 , то метод обратной матрицы применим.
, то метод обратной матрицы применим.
Используем формулу 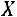

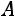

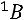 . Найдѐм обратную матрицу по формуле:
. Найдѐм обратную матрицу по формуле:
,
где 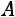 − определитель матрицы системы,
− определитель матрицы системы, 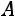


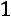

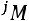 – алгебраические дополнения элементов матрицы
– алгебраические дополнения элементов матрицы
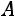 .
.
Вычислим алгебраические дополнения элементов матрицы 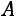 :
:

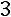


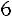

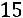

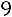 ;
;


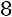 ;
;

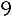

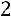

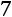 ;
;


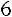 ;
;

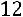

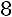

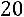 ;
;


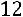 ;
;


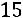




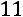 ;
;
48
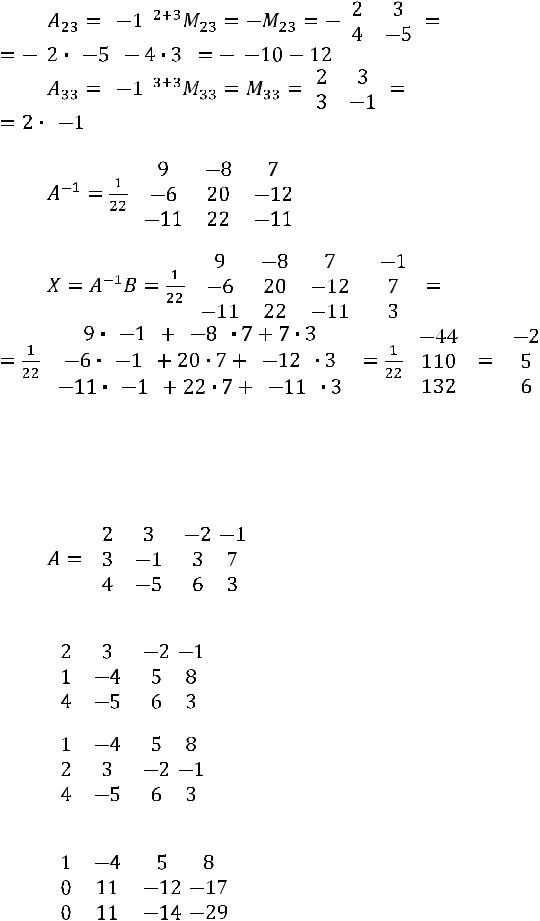

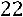 ;
;

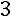




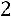

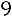


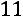 .
.
Составим обратную матрицу:
.
Найдѐм матрицу неизвестных X:
.
Ответ: 
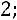
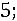
 . 3. Метод Гаусса.
. 3. Метод Гаусса.
Запишем расширенную матрицу системы и приведѐм еѐ к ступенчатому виду с помощью элементарных преобразований, приводящих к эквивалентной системе.
.
Выполним следующие преобразования.
1) Ко второй строке прибавим первую, умноженную на 
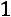 :
:
.
2) Поменяем первую и вторую строки местами:
.
3)Прибавим ко второй строке первую, умноженную на 
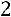 ;
;
ктретьей строке прибавим первую, умноженную на 
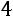 :
:
.
4) Прибавим к третьей строке вторую, умноженную на 
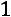 :
:
49
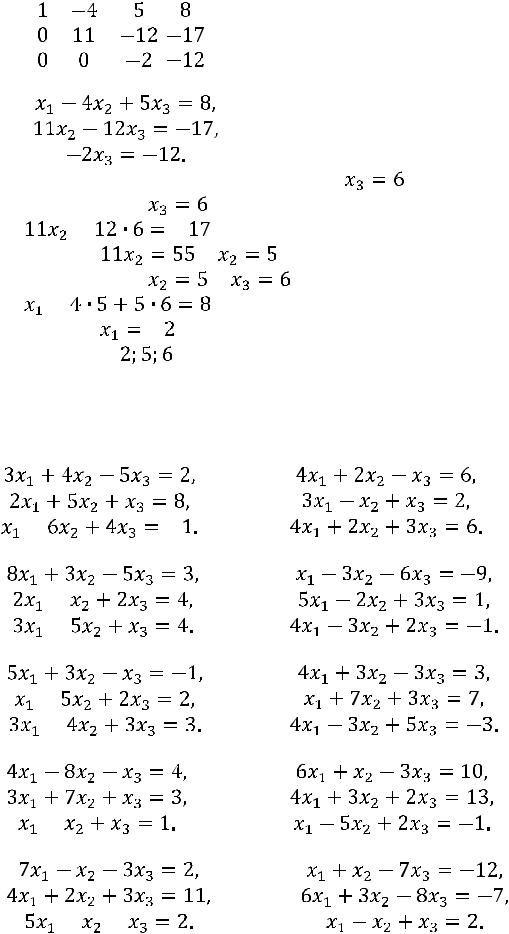
.
На основе последней матрицы запишем систему уравнений:
Из последнего уравнения находим |
. |
|||||||||||
Подставляем |
|
во второе уравнение: |
||||||||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда |
|
и |
. |
|
||||||||
Подставляем |
|
и |
в первое уравнение: |
|||||||||
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда |
|
|
. |
|
|
|
||||||
|
|
|
|
|||||||||
Ответ: |
|
|
. |
|
|
|||||||
|
|
|
||||||||||
Задание 9. Решить систему линейных алгебраических уравнений по правилу Крамера, методом обратной матрицы и методом Гаусса.
1. |
2. |
|||
|
|
|
|
|
3. |
|
4. |
|
||
|
|
|
5. |
|
|
6. |
|
|
|
|||
|
|
|
|
|
7. |
8. |
|
|
|
|
9. |
10. |
|||
|
|
|
|
|
50
