
898
.pdf
17. |
|
. |
18. |
|
. |
||||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
19. |
|
|
|
|
. |
20. |
|
|
|
|
. |
||||||||||
|
|
||||||||||||||||||||
21. |
|
|
|
|
|
|
22. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
. |
|
|
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
23. |
|
|
|
|
|
|
. |
24. |
|
. |
|||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
25. |
|
. |
26. |
|
|
|
|
|
|
|
. |
||||||||||
|
|
|
|||||||||||||||||||
27. |
|
|
|
28. |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
. |
|
|
|
|
|
|
|
|
|
. |
|||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
29. |
. |
30. |
|
|
|
|
|
|
. |
||||||||||||
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
31. |
|
|
|
. |
32. |
|
|
. |
|||||||||||||
|
|
|
|||||||||||||||||||
33. |
|
|
|
|
34. |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
. |
|
|
|
|
. |
||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
35. |
|
|
|
. |
36. |
|
|
. |
|||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
31

Миноры и алгебраические дополнения
|
элемента матрицы |
|
Справочный материал. |
|
|
Минором |
элемента |
матрицы называется определитель, |
полученный из матрицы вычѐркиванием i-й строки и j-ого столбца.
Алгебраическим дополнением элемента  матрицы называет-
матрицы называет-
ся число |
|
. |
|
Пример. Найти минор 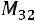 и алгебраическое дополнение
и алгебраическое дополнение 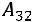
для данной матрицы: |
. |
Решение. 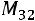 – это минор элемента матрицы, находящегося на пересечении третьей строки и второго столбца матрицы:
– это минор элемента матрицы, находящегося на пересечении третьей строки и второго столбца матрицы: 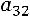


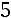 . Для нахождения указанного минора вычеркнем в матрице третью строку и второй столбец. Оставшиеся элементы запишем в определитель, который и является искомым минором:
. Для нахождения указанного минора вычеркнем в матрице третью строку и второй столбец. Оставшиеся элементы запишем в определитель, который и является искомым минором:


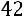

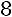


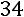 .
.
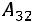 – это алгебраическое дополнение элемента матрицы, находящегося на пересечении третьей строки и второго столбца матрицы:
– это алгебраическое дополнение элемента матрицы, находящегося на пересечении третьей строки и второго столбца матрицы: 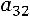


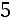 . Используем формулу для нахождения алгебраического дополнения:
. Используем формулу для нахождения алгебраического дополнения:

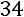 .
.
Ответ: 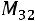


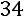 ,
, 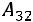

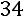 .
.
Задание 6. Найти указанные минор и алгебраическое дополнение для данной матрицы.
1. |
|
|
|
|
|
; |
, |
. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2. |
|
; |
, |
. |
|
3. |
|
; |
, |
. |
|
32
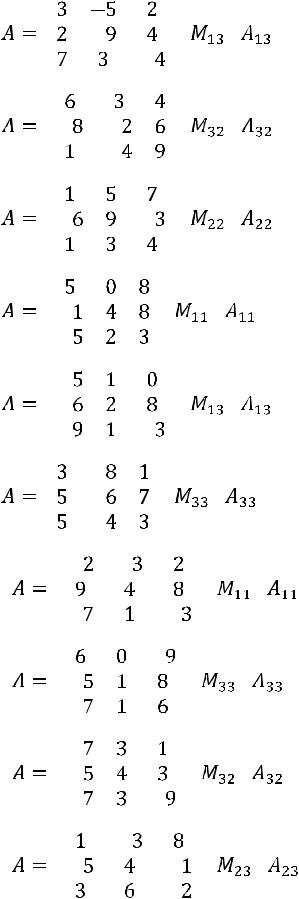
4. |
|
|
|
|
|
; |
, |
|
. |
||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
|
|
|
|
|
|
|
; |
, |
|
. |
||||||||
|
|
|
|
|
|
|
|||||||||||||
6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
. |
|||
|
|
|
|
|
|
|
|
|
; |
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||
7. |
|
|
|
|
; |
|
, |
. |
|
||||||||||
|
|
|
|
|
|||||||||||||||
8. |
|
|
|
|
; |
, |
|
. |
|||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|||||||||||||||
9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
; |
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
10. |
|
|
|
|
; |
|
, |
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
11. |
|
|
|
|
; |
, |
|
. |
|||||||||||
|
|
|
|
|
|||||||||||||||
12. |
|
|
|
|
; |
, |
|
. |
|||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|||||||||||||||
13. |
|
|
|
|
|
|
|
|
, |
. |
|||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
; |
|
||||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
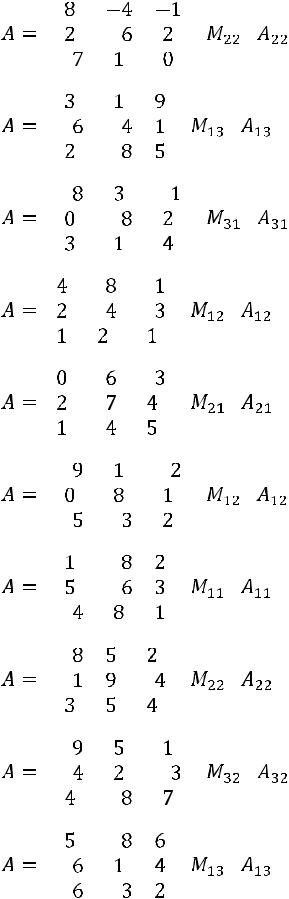
14. |
|
|
|
|
|
; |
, |
. |
||||
|
||||||||||||
15. |
|
|
|
|
|
|
|
|
|
, |
. |
|
|
|
|
|
|
; |
|||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16. |
|
|
|
|
|
; |
, |
. |
||||
|
|
|
|
|
||||||||
17. |
|
|
|
|
|
|
; |
, |
. |
|||
|
|
|
|
|
|
|||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||
18. |
|
|
|
|
; |
, |
. |
|||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
19. |
|
|
|
|
; |
, |
. |
|||||
20. |
|
|
|
|
|
|
, |
. |
||||
|
|
|
|
|
||||||||
|
|
|
|
|
; |
|||||||
|
|
|
|
|
||||||||
21. |
|
|
|
|
|
, |
. |
|||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
; |
||||||
|
|
|
|
|
||||||||
22. |
|
|
|
|
|
, |
. |
|||||
|
|
|
|
|
|
; |
||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
23. |
|
|
|
|
; |
, |
. |
|||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
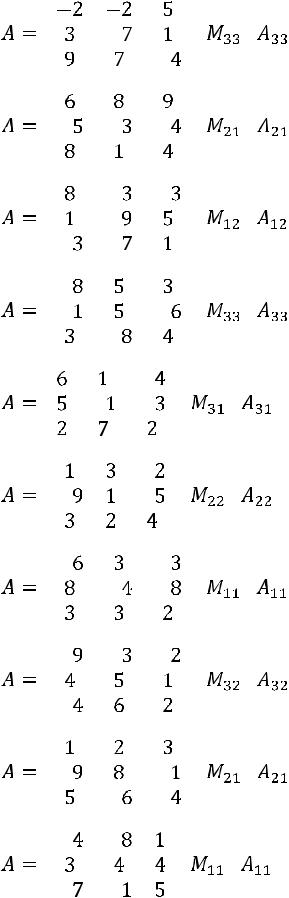
24. |
|
|
|
|
|
; |
, |
. |
||||
|
||||||||||||
25. |
|
|
|
|
|
|
|
, |
. |
|||
|
|
|
|
|
|
|
|
|
; |
|||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
26. |
|
|
|
|
|
; |
, |
. |
||||
|
|
|
|
|
||||||||
27. |
|
|
|
|
|
|
|
|
, |
. |
||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
; |
||||
|
|
|
|
|
||||||||
28. |
|
|
|
|
|
|
|
|
, |
. |
||
|
|
|
|
|
||||||||
|
|
|
|
|
|
; |
||||||
|
|
|
|
|
||||||||
29. |
|
|
|
|
|
, |
. |
|||||
|
|
|
|
|
|
; |
||||||
|
|
|
|
|
||||||||
30. |
|
|
|
|
|
, |
. |
|||||
|
|
|
|
|
|
|
; |
|||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
31. |
|
|
|
|
; |
, |
. |
|||||
32. |
|
|
|
|
|
, |
. |
|||||
|
|
|
|
|
|
; |
||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
33. |
|
|
|
|
; |
, |
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
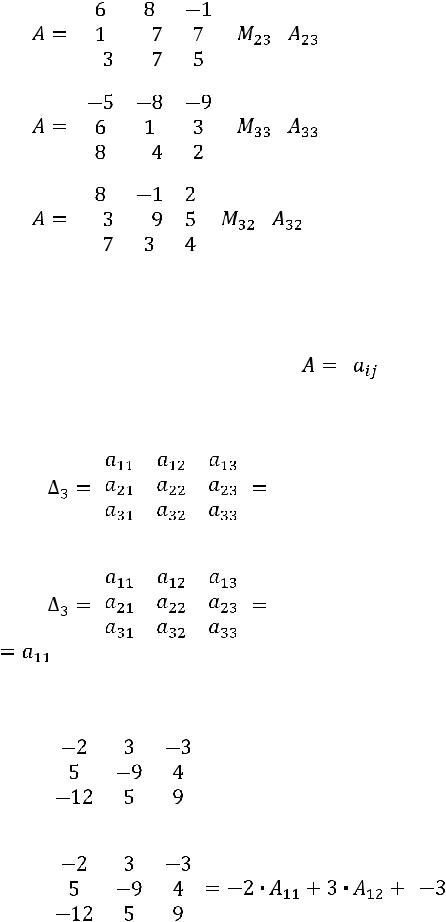
34. |
|
|
|
; |
, |
. |
|
||||||
|
|
|
|
|
|
|
35. |
; |
, |
. |
|
|
|
|
|
|
36. |
|
|
|
; |
, |
. |
|
|
|||||
|
|
|
|
|
|
|
Вычисление определителя матрицы третьего порядка разложением по строке или столбцу
Справочный материал.
Определителем матрицы |
третьего порядка, или |
определителем третьего порядка, называется число, равное сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:



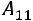

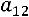

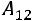



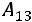 (разложение по первой строке) или
(разложение по первой строке) или

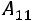

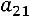

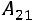

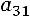

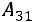 (разложение по первому столбцу).
(разложение по первому столбцу).
Пример. Вычислить определитель третьего порядка разложением по строке или столбцу:
.
Решение. Вычислим определитель третьего порядка разложением, например, по первой строке:

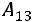 .
.
Вычислим алгебраические дополнения:
36



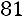

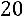


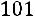 .
.


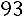 .
.

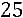

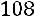


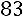 .
.
Окончательно получаем:

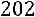

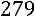

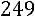

 .
.
Задание 7. Вычислить определитель третьего порядка разложением по строке или столбцу.
1. |
. |
2. |
|
|
|
. |
|
|
|||||||
|
|
|
|
|
|
|
|
3. |
|
. |
4. |
|
|
|
. |
||
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
5. |
|
. |
6. |
|
|
|
. |
|
|
|
|||||
|
|
|
|
|
|
|
|
7. |
|
8. |
|
. |
||||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
9. |
|
. |
10. |
. |
|||
|
|||||||
|
|
|
|
|
|
|
|
11. |
. |
12. |
|
. |
|||||
|
|||||||||
|
|
|
|
|
37 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|

13. |
|
|
|
|
. |
14. |
. |
||||||||||||||||
15. |
|
|
|
|
|
|
|
|
|
|
|
|
16. |
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17. |
|
|
|
|
|
|
|
|
|
|
|
|
18. |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
19. |
|
|
|
|
|
|
|
|
. |
20. |
|
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
21. |
|
|
|
|
|
|
|
22. |
|
|
|
|
|
||||||||||
|
|
|
|
|
. |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
. |
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
23. |
|
|
|
|
|
|
|
|
|
|
24. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
. |
|
|
|
. |
|||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
25. |
|
|
|
|
|
|
. |
26. |
. |
||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
27. |
|
|
|
|
. |
28. |
. |
||||||||||||||||
|
|
|
|
||||||||||||||||||||
29. |
|
|
|
|
. |
30. |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
. |
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
31. |
|
|
|
|
. |
32. |
|
|
|
. |
|||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
38

33. |
|
|
|
. |
34. |
|
|
|
. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
35. |
. |
36. |
|
|
|
. |
|||
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
Обратная матрица Справочный материал.
Если 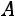 – квадратная матрица, то обратной для неѐ называется матрица, обозначаемая
– квадратная матрица, то обратной для неѐ называется матрица, обозначаемая 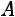

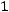 и удовлетворяющая условиям:
и удовлетворяющая условиям:


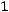





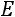 ,
,
где Е – единичная матрица.
Теорема. Обратная матрица существует тогда и только тогда, когда исходная матрица 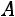 невырожденная (определитель матрицы
невырожденная (определитель матрицы 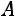 не равен нулю).
не равен нулю).
Обратную матрицу можно найти двумя способами.
Первый способ (с помощью присоединѐнной матрицы).


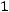

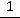

 , где
, где 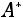 – присоединѐнная матрица (получена
– присоединѐнная матрица (получена
транспонированием матрицы, составленной из алгебраических дополнений 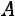 элементов
элементов 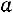 матрицы
матрицы 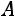 ).
).
Можно записать:
.
Второй способ (с помощью элементарных преобразований). К
матрице 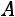 размерности
размерности 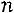

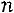 приписывают справа единичную матрицу размерности
приписывают справа единичную матрицу размерности 

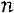 . Получают прямоугольную матрицу
. Получают прямоугольную матрицу 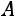
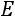 размерности
размерности 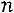

 . С помощью элементарных преобразований над строками матрицу
. С помощью элементарных преобразований над строками матрицу 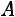
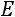 приводят к ступенчатому виду
приводят к ступенчатому виду 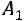
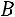 , где
, где 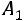
– треугольная матрица; затем матрицу 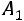
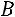 приводят к виду
приводят к виду 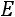
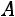

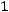

Элементарные преобразования матрицы.
1.Отбрасывание нулевой строки (столбца) матрицы.
2.Умножение всех элементов строки (столбца) матрицы на число, не равное 0.
3.Изменение порядка строк (столбцов) матрицы.
39
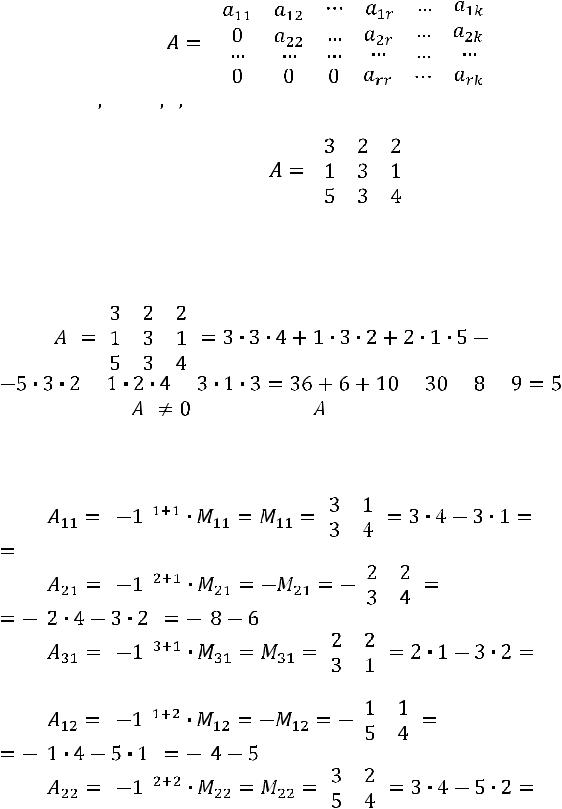
4.Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца).
5.Транспонирование матрицы.
С помощью элементарных преобразований матрицу можно привести к ступенчатому виду (элементы, расположенные ниже главной диагонали, равны нулю):
,
где 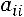
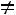
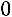
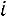

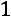

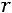
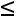
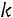 .
.
Пример. Дана матрица |
. Найти для неѐ обрат- |
ную 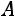

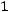 .
.
Решение.
Первый способ.
Вычислим определитель матрицы 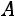 :
:
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||
Так как |
|
, то матрица – невырожденная и для неѐ су- |
||||||||
ществует обратная.
Найдѐм алгебраические дополнения всех элементов матрицы
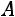 .
.
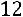

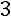

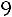 ;
;


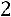 ;
;

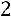

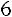


 ;
;

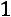 ;
;
40
