
898
.pdf
решений. Придадим переменной 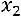 значение
значение 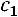 , тогда
, тогда 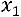


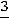
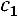 . Таким образом, собственный вектор матрицы, соответствующий собственному значению
. Таким образом, собственный вектор матрицы, соответствующий собственному значению 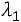


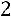 имеет вид:
имеет вид: 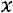
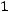


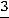
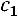

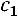 .
.
Найдѐм собственный вектор, соответствующий собственному значению 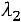

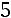 . Для этого значение
. Для этого значение 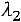

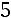 подставляем в уравне-
подставляем в уравне-
ние |
|
. Откуда |
получаем |
|
|
|
или |
|||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
или |
|
Одно из уравнений системы |
||||
можно отбросить и получаем 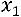

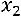

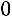 . Система имеет бесконечное множество решений. Придадим переменной
. Система имеет бесконечное множество решений. Придадим переменной 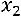 значение
значение 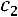 , тогда
, тогда 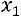

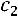 . Таким образом, собственный вектор матрицы, соответствующий собственному значению
. Таким образом, собственный вектор матрицы, соответствующий собственному значению 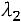

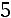 имеет вид:
имеет вид:
.
Ответ: |
|
, |
|
|
|
; |
, |
. |
|
|
|
Задание 20. Найти собственные значения и собственные векторы матрицы.
1. |
|
|
|
2. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
3. |
4. |
|||||||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
5. |
6. |
|||||||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
7. |
8. |
|||||||||||
9. |
10. |
|||||||||||
|
|
|
|
|
|
|||||||
11. |
12. |
|||||||||||
|
|
|
|
|||||||||
13. |
14. |
|||||||||||
111

15. |
|
|
|
|
16. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17. |
|
18. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
19. |
|
20. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
21. |
|
22. |
|
|
|
|
|
|
||||||||
23. |
|
24. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
25. |
|
26. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
27. |
|
28. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
29. |
|
30. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
31. |
|
32. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
33. |
|
34. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
35. |
|
36. |
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Линейная модель обмена Справочный материал.
Линейной моделью обмена является матричное уравнение
или, что одно и то же, |
|
|
, где |
– |
|
|
|
||||
структурная матрица торговли, |
|
– доля национального дохода, |
|||
которую страна |
тратит на покупку товаров у страны |
, причѐм |
|||
|
; |
|
|
– вектор национальных |
|
доходов стран |
; |
|
– единичная матрица, |
||
|
|
112 |
|
|
|
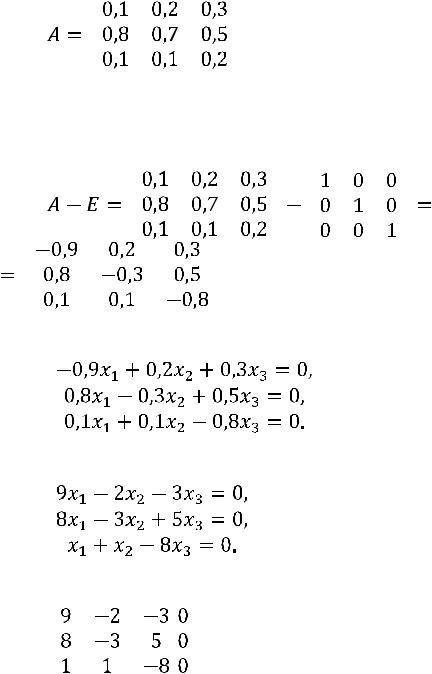
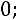
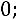


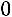 – нулевой вектор. Решить уравнение
– нулевой вектор. Решить уравнение 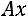

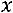 означает найти собственный вектор
означает найти собственный вектор 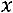 , соответствующий собственному значению
, соответствующий собственному значению 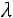

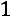 .
.
Пример. Найти соотношение национальных доходов трѐх стран для сбалансированной торговли, если задана структурная матрица торговли 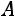 :
:
Решение.
Найдѐм собственный вектор 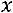 , отвечающий собственному значению
, отвечающий собственному значению 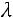

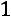 . Для этого решим уравнение
. Для этого решим уравнение 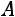

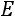
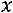

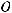 . Запишем матрицу
. Запишем матрицу 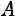

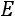 :
:
.
Тогда уравнение 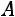

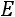
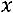

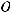 можно записать в виде следующей однородной системы линейных алгебраических уравнений:
можно записать в виде следующей однородной системы линейных алгебраических уравнений:
Избавимся от десятичных дробей. Для этого умножим первое уравнение на 
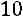 , второе и третье на 10:
, второе и третье на 10:
Решим систему методом Гаусса. Запишем расширенную матрицу системы:
.
Приведѐм расширенную матрицу системы к ступенчатому ви-
ду.
1) Поменяем местами первую и третью строки:
113

.
2) Прибавим ко второй строке первую, умноженную на 
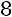 , прибавим к третьей строке первую, умноженную на
, прибавим к третьей строке первую, умноженную на 
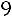 :
:
.
3) Прибавим к третьей строке вторую, умноженную на 
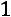 :
:
.
4) Вычеркнем нулевую строку:
.
5) Умножим вторую строку на 
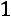 :
:
.
Так как ранг матрицы системы равен 2 и ранг расширенной матрицы системы равен 2, то система совместна. И так как число неизвестных равно 3, то есть ранг меньше числа неизвестных, то система имеет бесконечное множество решений.
Запишем систему уравнений по виду последней матрицы:
Объявляем неизвестные 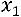
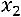 основными, неизвестную
основными, неизвестную 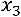 свободной. Выразим основные неизвестные через свободную. Из
свободной. Выразим основные неизвестные через свободную. Из
второго уравнения 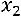

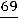
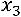 . Из первого уравнения
. Из первого уравнения 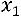

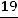
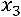 . Переобозначим неизвестное
. Переобозначим неизвестное 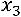 через c. Тогда решением системы яв-
через c. Тогда решением системы яв-
ляется вектор |
|
|
|
. Полученный результат означает, |
|
|
что сбалансированность торговли трѐх стран достигается при соотношении национальных доходов стран 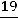
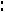
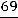
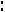
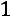 или
или 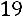
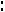
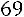
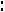
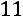 .
.
Ответ: 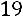
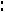
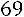
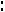
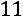 .
.
114
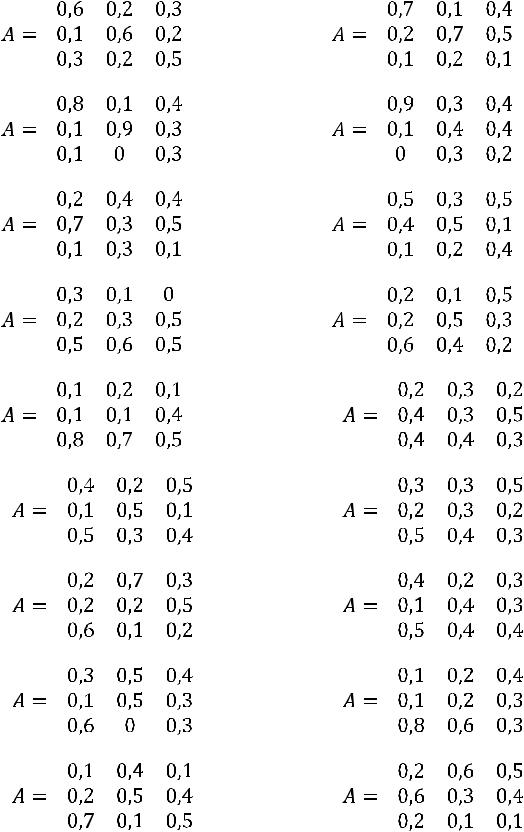
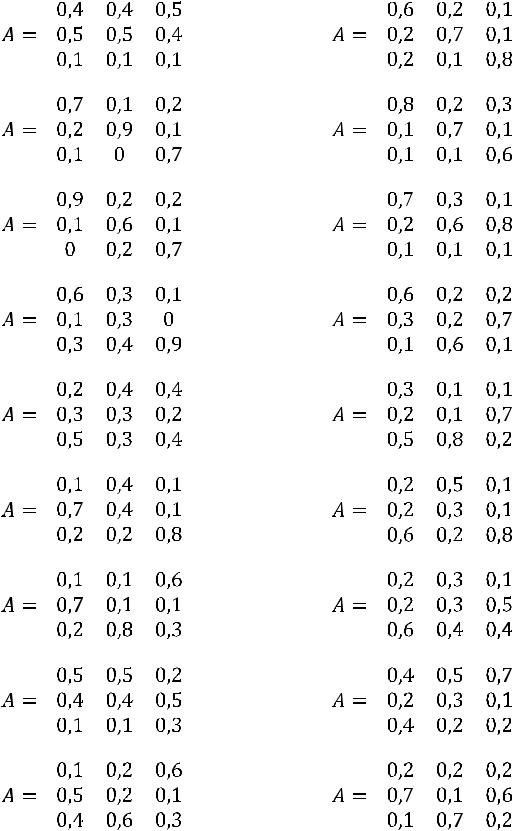
Задание 21. Найти соотношение национальных доходов трѐх стран для сбалансированной торговли, если задана структурная матрица торговли 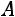 .
.
1. |
2. |
3. |
4. |
5. |
6. |
7. |
8. |
9. |
10. |
11. |
12. |
13. |
14. |
15. |
16. |
17. |
18. |
115
19. |
20. |
21. |
22. |
23. |
24. |
25. |
26. |
27. |
28. |
29. |
30. |
31. |
32. |
33. |
34. |
35. |
36. |
116
Приведение квадратичной формы к каноническому виду
Справочный материал. |
|
Квадратичной формой |
от n переменных назы- |
вается сумма, каждое слагаемое которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:
|
. |
|
Коэффициенты |
квадратичной формы |
– действительные |
числа, причѐм |
. Матрица |
, составлен- |
ная из этих коэффициентов, называется матрицей квадратичной формы.
В матричной записи квадратичная форма имеет вид:
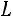

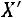
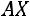 ,
,
где 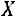

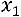
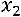

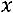
 – матрица-столбец переменных,
– матрица-столбец переменных, 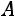 – матрица квадратичной формы.
– матрица квадратичной формы.
Квадратичная форма называется канонической, если все еѐ ко-
эффициенты |
при |
: |
|
|
. |
Канонический вид квадратичной формы не является однозначно определѐнным.
Пример. Привести квадратичную форму 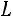 к каноническому виду:
к каноническому виду:

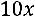
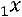
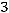

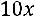
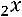
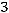 .
.
Решение.
Выполним следующие преобразования:
117
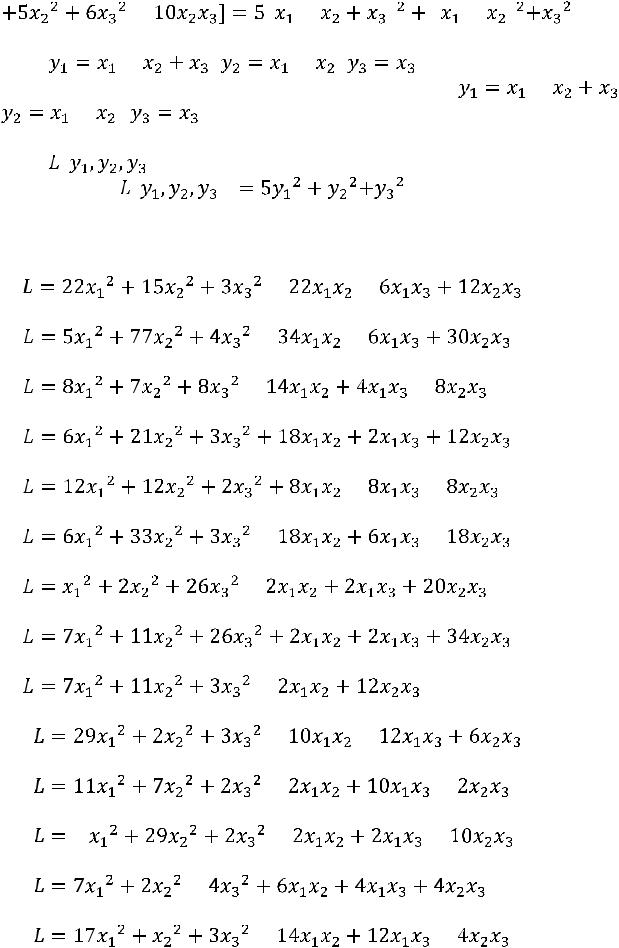
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||
Выполним переобозначения: |
|
|
|||||||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
, |
|
|
, |
. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Полученное |
линейное |
преобразование |
|
|
, |
||||||||||||
|
|||||||||||||||||
|
|
, |
|
|
|
|
приводит квадратичную форму к следующе- |
||||||||||
|
|
|
|
|
|||||||||||||
му каноническому виду:

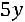
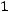
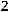


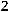
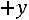
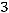
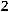 .
.
Ответ: |
. |
Задание 22. Привести квадратичную форму к каноническому виду.
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
4. |
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||||
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
7. |
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||
8. |
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||||
9. |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
12. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
13. |
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
14. |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
118 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
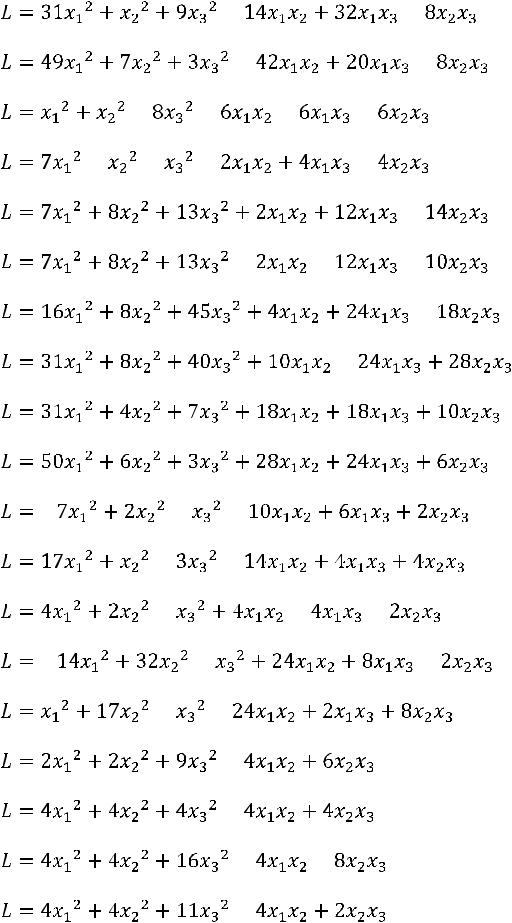
15. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
16. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
17. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
18. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
19. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
20. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
21. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
22. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
23. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||||||||
24. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||||||||
25. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
26. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
27. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
28. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
29. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
30. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
31. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
32. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
33. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
119 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
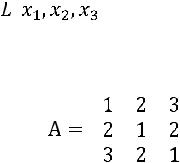
34. 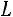

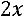
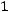
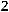

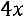
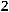
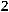

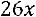
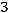
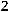

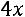
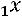
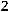

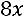
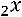
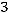 .
.
35. 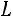

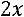
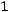
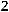

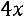
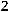
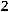

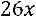
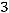
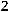

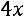
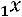
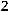

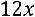
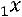
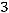

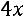
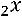
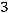 .
.
36. 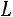

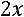
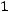
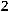

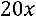
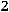
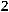

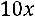
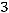
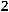

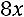
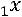
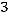

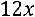
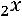
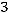 .
.
Знакоопределённость квадратичной формы
Нормальным видом квадратичной формы называют сумму квадратов нескольких неизвестных с коэффициентами +1 или –1.
Квадратичная форма L от n неизвестных с действительными коэффициентами называется положительно определѐнной, если она приводится к нормальному виду, состоящему из n положительных квадратов.
Квадратичная форма L от n неизвестных с действительными коэффициентами называется отрицательно определѐнной, если она приводится к нормальному виду, состоящему из n отрицательных квадратов.
Квадратичная форма 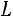

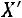
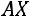 положительно определена то-
положительно определена то-
гда и только тогда, когда: все собственные значения матрицы 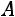 положительны или все главные миноры матрицы
положительны или все главные миноры матрицы  положительны
положительны
(Критерий Сильвестра).
Квадратичная форма 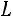

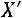
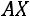 отрицательно определена то-
отрицательно определена то-
гда и только тогда, когда: все собственные значения матрицы 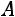 отрицательны или все главные миноры матрицы
отрицательны или все главные миноры матрицы 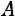 нечѐтного порядка отрицательны, а чѐтного порядка положительны (Критерий Силь-
нечѐтного порядка отрицательны, а чѐтного порядка положительны (Критерий Силь-
вестра).
Пример. Исследовать квадратичную форму 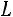 на знакоопределѐнность:
на знакоопределѐнность:

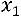
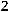

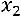
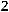

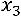
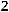

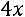
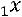
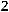

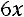
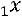
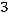

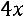
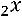
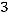 .
.
Решение.
Первый способ. (С помощью собственных значений.)
Запишем матрицу квадратичной формы:
.
Найдѐм собственные значения матрицы 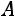 . Для этого составим характеристическое уравнение:
. Для этого составим характеристическое уравнение:
120
