898
.pdf
14.
15.
16.
17.
18.
19.
20.
91
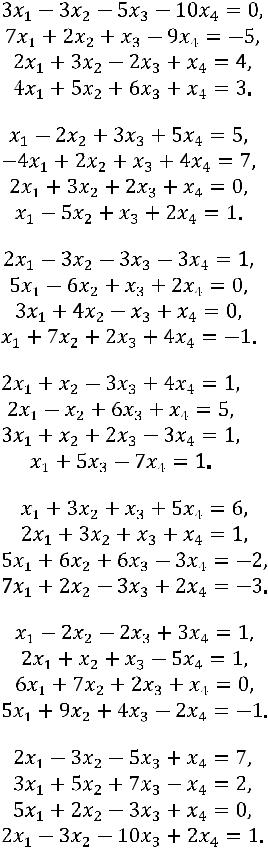
21.
22.
23.
24.
25.
26.
27.
92
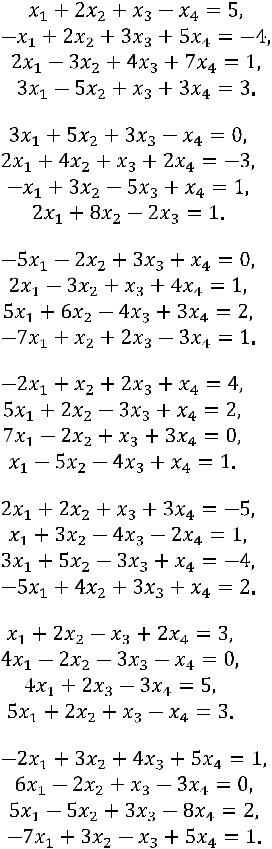
28.
29.
30.
31.
32.
33.
34.
93
35.
36.
Решение систем линейных алгебраических уравнений методом Гаусса
Справочный материал.
Для решения системы методом Гаусса необходимо привести расширенную матрицу системы к ступенчатому виду. Далее указать ранг матрицы системы и расширенной матрицы системы.
Если ранги не совпадают, то по теореме Кронекера – Капелли система не имеет решения.
Если ранг матрицы системы равен рангу расширенной матрицы системы и равен числу неизвестных: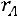 
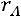
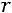
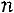, то систе-
ма имеет единственное решение.
Если ранг матрицы системы равен рангу расширенной матрицы системы и меньше числа неизвестных: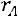 
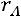
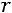
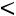
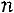, то си-
стема имеет бесконечное множество решений. В этом случае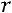 
пе-
ременных, определитель матрицы коэффициентов при которых отличен от нуля, объявляют основными переменными; остальные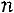 
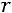переменных объявляют свободными. Свободным переменным можно придать любое числовое значение. Затем основные неизвестные выражают через свободные неизвестные. Формулы, полученные для нахождения основных неизвестных, называют общим решением. На основании общего решения, придавая свободной неизвестной любое числовое значение, получают бесконечное множе-
ство частных решений.
94
Пример. Решить систему линейных алгебраических уравнений методом Гаусса:
Решение. Запишем расширенную матрицу системы:
.
Приведѐм расширенную матрицу к ступенчатому виду. Для этого выполним следующие преобразования.
1) Поменяем местами первую и вторую строки:
.
2) Прибавим ко второй строке первую, умноженную на 
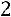; прибавим к третьей строке первую, умноженную на 
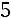; прибавим к четвѐртой строке первую, умноженную на 
:
.
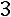3) Умножим вторую строку на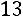 
, третью строку умножим на
:
.
4) Прибавим к третьей строке вторую, вторую строку обратно разделим на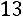 
:
.
5) Умножим вторую строку на 
, четвѐртую строку умножим на 
:
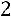95
.
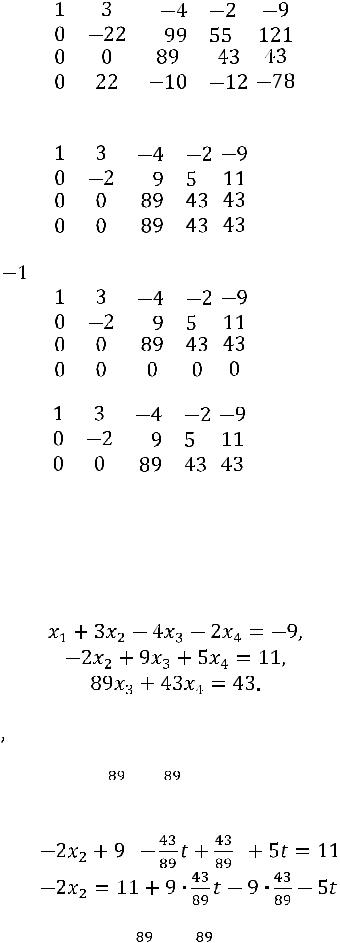
6) Прибавим к четвѐртой строке вторую, вторую строку обратно разделим на 
:
.
7) Прибавим к четвѐртой строке третью, умноженную на
:
.
8) Вычеркнем нулевую строку:
.
Матрица приведена к ступенчатому виду. Количество ненулевых строк матрицы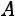 
равно 3, поэтому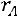 
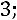количество ненулевых строк матрицы 
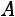равно 3, поэтому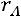 
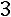. По теореме Кронекера−Капелли система совместна. Так как ранг меньше числа неизвестных, то система имеет бесконечное множество решений.
На основе последней матрицы запишем систему уравнений:
Объявим неизвестную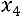 
свободной и обозначим еѐ через 
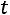
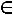
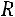. Выразим из третьего уравнения 
через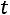 
:
.
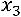
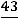
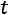
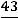Подставим выражение для переменной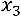 
во второе уравнение и выразим 
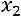через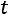 
:
.
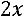
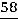
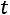
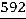96
Окончательно:
.
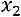
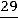
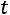
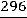Подставим выражения для переменных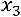 
и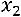 
в первое уравнение и выразим 
через 
:
Окончательно:
.
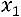
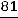
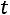
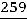Таким образом, получаем общее решение:
.
Найдѐм одно частное решение. Для этого придадим свободной неизвестной числовое значение, например,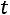 
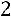. Получим частное
решение: |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
общее решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
частное решение: |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Задание 17. Решить систему линейных алгебраических уравнений методом Гаусса.
1.
2.
3.
97
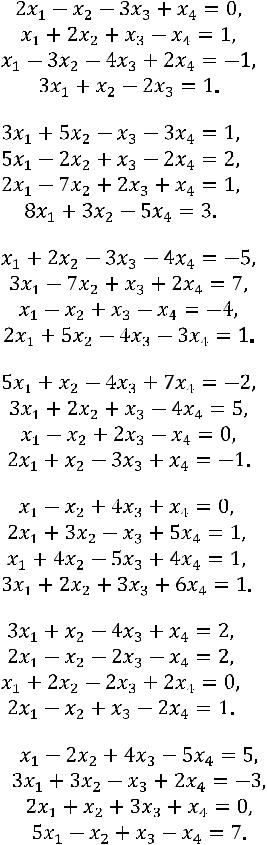
4.
5.
6.
7.
8.
9.
10.
98
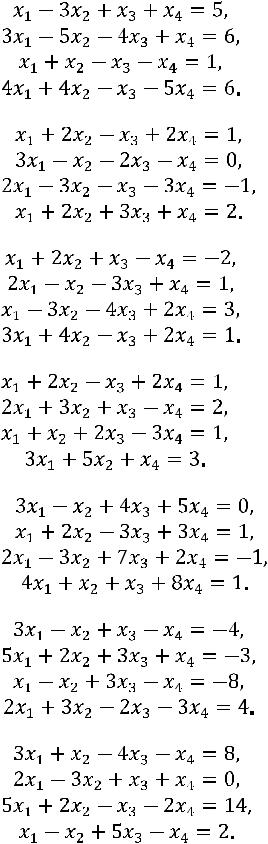
11.
12.
13.
14.
15.
16.
17.
99
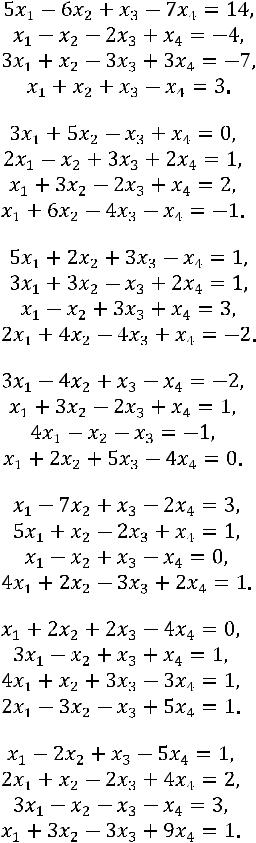
18.
19.
20.
21.
22.
23.
24.
100