
659
.pdf
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
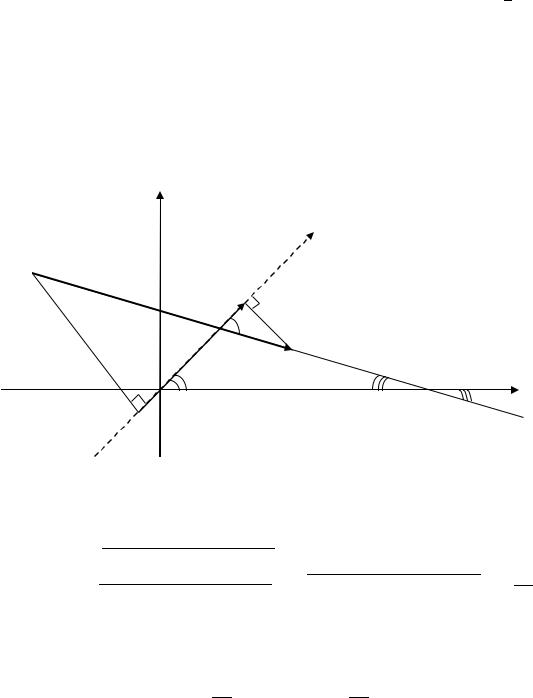
Рис. 2.12. Проекция направленного отрезка на ось |
||||||||
|
|
|
̅̅̅̅̅̅̅̅ |
|
|
|
|
|
̅̅̅̅̅̅̅̅ |
|
пр 1 2 |
|
. |
|
|
|
|
= пр 1 2. Тогда sin = |
|
̅̅̅̅̅̅̅̅ |
|
|
|
|||
|
|
|
| 1 2| |
|
|
|
|
|
Отсюда: |
|
|
|
|
|
|
|
|
|
|
|
̅̅̅̅̅̅̅̅ |
= | 1 |
2| sin . |
|||
|
|
|
пр 1 |
2 |
||||
Таким образом, |
проекция направленного отрезка на ось равна |
|||||||
произведению длины этого отрезка на синус угла, образуемого отрезком с осью . Или этот результат можно интерпретировать следующим образом: проекция направленного отрезка на ось равна произведению длины этого отрезка на косинус угла, образуемого отрезком с осью .
|
Из |
|
|
|
|
|
|
̅̅̅̅̅̅̅̅ |
= |
| 1 2| cos |
|
|
̅̅̅̅̅̅̅̅ |
= | 1 2| sin |
||||
|
формул пр 1 |
2 |
|
|
и пр 1 2 |
|||||||||||||
можно получить формулу нахождения полярного угла |
̅̅̅̅̅̅̅̅ |
|||||||||||||||||
отрезка 1 2. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̅̅̅̅̅̅̅̅ |
|
|||
Выразим из каждой формулы длину отрезка 1 |
2: |
|
||||||||||||||||
|
|
|
|
|
̅̅̅̅̅̅̅̅ |
|
|
|
̅̅̅̅̅̅̅̅ |
|
|
|
|
|||||
|
| | = |
пр 1 2 |
|
и | |
| = |
пр 1 2 |
. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||||
1 |
2 |
|
|
cos |
1 |
2 |
|
sin |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Приравняем полученные выражения: |
|
|
|
|
|||||||||||||
|
̅̅̅̅̅̅̅̅ |
|
|
̅̅̅̅̅̅̅̅ |
|
|
|
|
|
|
|
|
|
|
||||
|
пр 1 2 |
= |
пр 1 2 |
. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
cos |
|
|
sin |
|
|
|
|
|
|
|
|
|
̅̅̅̅̅̅̅̅ |
||||
|
Умножив полученное равенство на sin |
|
||||||||||||||||
|
и разделив на пр 1 2, по- |
|||||||||||||||||
лучаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
̅̅̅̅̅̅̅̅ |
|
|
|
|
|
|
|
|
|
|
|||||
|
= |
пр 1 2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||
|
cos |
̅̅̅̅̅̅̅̅ |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
пр 1 2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
Отсюда, учитывая формулы нахождения проекции отрезка на оси ко- |
|||||||||||||||||
ординат через координаты начала и конца отрезка, можно записать: |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
2− 1 |
. |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||
Полученная формула позволяет находить полярный угол отрезка по известным координатам его начала и конца.
Пример 2.9. Вычислить проекции отрезка на координатные оси, зная, что длина отрезка равна 2, полярный угол равен 6 .
Решение.
Найдём проекцию отрезка на ось :
31
̅̅̅̅̅̅̅̅ |
= | 1 2 |
| cos = 2 cos |
|
|
|
|
|
|||||
= |
√3. |
|||||||||||
|
|
|||||||||||
пр 1 2 |
6 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
Найдём проекцию отрезка на ось : |
|
|
|
|||||||||
̅̅̅̅̅̅̅̅ |
= | 1 2 |
| sin = 2 sin |
|
= 1. |
|
|
||||||
пр 1 2 |
|
|
|
|
|
|||||||
|
̅̅̅̅̅̅̅̅ |
|
|
̅̅̅̅̅̅̅̅6 |
|
|
|
|
||||
|
|
|
|
|
|
|
||||||
Ответ: пр 1 2 = √3, пр 1 2 |
= 1. |
|
|
|||||||||
Пример 2.10. Даны две точки (−5; 2) и (3; 1). Найти проекцию отрезка ̅̅̅̅ на ось, которая составляет с осью абсцисс угол = 43.
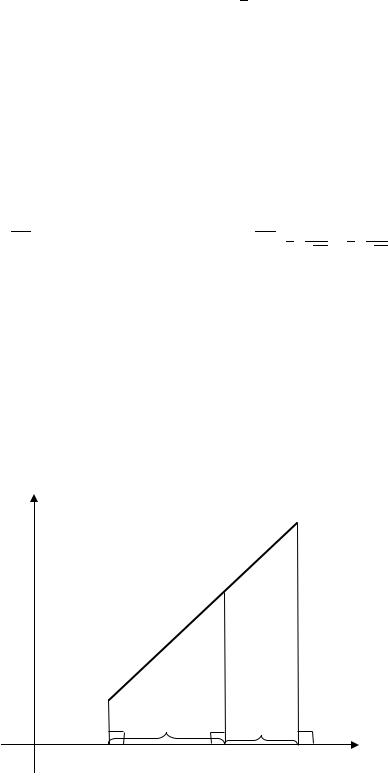
Решение. Обозначим через ось, которая составляет с осью абсцисс заданный угол . Ось проведём через начало координат. Обозначим черезполярный угол отрезка ̅̅̅̅, то есть угол между отрезком ̅̅̅̅ и осью . Обозначим через полярный угол отрезка ̅̅̅̅ относительно новой оси , то есть угол между отрезком ̅̅̅̅ и осью Опустим из точек и перпендикуляры на ось . Основания перпендикуляров обозначим через ′ и
′ соответственно. Проекцией отрезка ̅̅̅̅ на ось является величина направленного отрезка ̅̅̅̅̅̅′ ′ (рис. 2.13).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
||
|
|
|
|
Рис. 2.13. Проекция отрезка ̅̅̅̅ на ось (к Примеру 2.10)
Применяя формулу нахождения проекции отрезка на ось через полярный угол, получаем: пр ̅̅̅̅ = | | cos . Найдём длину отрезка ̅̅̅̅ по
формуле: = √( 2 − 1)2 + ( 2 − 1)2. Тогда:
| | = √( 2 − 1)2 + ( 2 − 1)2 = √(3 − (−5))2 + (1 − 2)2 = √65.
Из чертежа (рис. 2.13) найдём полярный угол :
= − = − ( − − ) = + .
Запишем проекцию отрезка ̅̅̅̅ на ось с учётом выполненных рас-
суждений:
пр ̅̅̅̅ = | | cos = √65 cos( + ) = √65(cos cos − sin sin ).
Найдём полярный угол из формулы нахождения полярного угла отрезка через координаты начала и конца отрезка:
32
= |
2− 1 |
= |
1−2 |
|
= − |
1 |
. |
|
|
3−(−5) |
|
||||||
|
− |
1 |
|
8 |
||||
2 |
|
|
|
|
|
|
||
Угол найдём из условия задачи: = 43 .
Далее найдём cos , cos , sin , sin , учитывая, что углы и – острые. Поэтому cos , cos , sin , sin – положительные величины. Найдём эти величины, используя формулы тригонометрии:
1 |
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
8 |
|
|||||||||||
cos = |
|
|
= |
|
|
|
|
|
|
= |
|
|
; cos = |
|
|
|
|
= |
|
|
|
= |
|
|
; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
√1+ 2 |
|
|
|
4 2 |
5 |
|
√1+ 2 |
1 |
2 |
√65 |
|||||||||||||||||||||||||
|
|
|
|
|
√1+( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√1+(− ) |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√1 − ( |
3 |
)2 |
= |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
sin = √1 − 2 = |
; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
√1 − ( |
|
8 |
)2 |
|
|
|
|
1 |
. |
|
|
|
|
|
|
|
|
||||||||||
sin = √1 − 2 = |
= |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√65 |
|
|
|
|
|
√65 |
|
|
|
|
|
|
|
|
|||||||
Тогда искомая проекция:
пр ̅̅̅̅ = √65(cos cos − sin sin ) = √65 (35 ∙ √865 − 45 ∙ √165) = 4. Ответ: пр ̅̅̅̅ = 4.
2.4. Деление отрезка в заданном отношении на плоскости
|
Пусть 1( 1; 1) и 2( 2; 2) – две данные точки на плоскости и из- |
|||
|
|
|
̅̅̅̅̅̅̅̅ |
|
вестно, что некоторая точка ( ; ) делит отрезок 1 2 в отношении , то |
||||
есть |
1 |
= . Здесь 1 и 2 |
|
̅̅̅̅̅̅ |
2 |
– величины направленных отрезков 1 и |
|||
̅̅̅̅̅̅̅ |
|
|
|
|
2. |
|
|
|
|
|
Получим формулы для вычисления координат точки . |
Для этого |
||
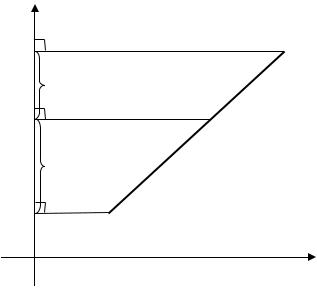
опустим перпендикуляры из точек 1, 2, на ось . Основания перпен-
дикуляров обозначим |
, |
, соответственно (рис. 2.14). |
1 |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
− 1 |
2 |
− |
|
|
1 |
|
|
|
|
|
2 |
|
Рис. 2.14. Нахождение абсциссы точки , которая делит отрезок ̅̅̅̅̅̅̅̅
1 2
в заданном отношении
33
Из элементарной геометрии известно, что отрезки прямых, заклю-
чённые между параллельными прямыми, пропорциональны, |
то есть |
1 |
= |
|||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
= . |
Но = − , |
|
|
= |
− . Тогда: |
|
1 |
|
= . Выразим |
|||||||||||||||||||||
|
|
|
− |
|||||||||||||||||||||||||||||
|
|
1 |
|
1 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
отсюда |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
− 1 = ( 2 − ) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
− 1 = 2 − |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
+ = 1 + 2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
(1 + ) = 1 + 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
= |
1+ 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полученная формула позволяет вычислить координату точки . |
||||||||||||||||||||||||||||||
|
|
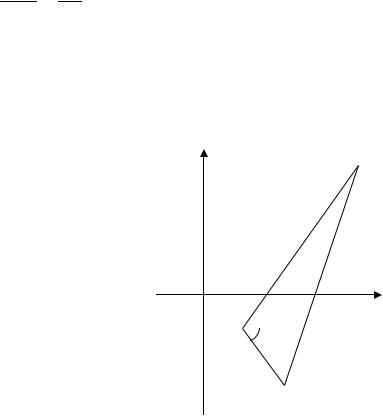
Далее опустим перпендикуляры из точек 1, 2, на ось . Осно- |
||||||||||||||||||||||||||||||
вания перпендикуляров обозначим |
, , соответственно (рис. 2.15). |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
− 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̅̅̅̅̅̅̅̅ |
|||
|
Рис. 2.15. Нахождение ординаты точки , которая делит отрезок 1 2 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
в заданном отношении |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Запишем пропорциональность отрезков: |
1 |
|
|
|
= |
1 |
|
|
= . |
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
2 |
|
|
|
|
2 |
|
|
|
||||||||
Но |
|
= − , |
= − . Тогда: |
= . Выразим отсюда : |
||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||
|
1 |
|
1 |
2 |
2 |
|
|
|
|
|
|
|
2− |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
− 1 = ( 2 − ) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
− 1 = 2 − |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
+ = 1 + 2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
(1 + ) = 1 |
|
+ 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
= |
1+ 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полученная формула позволяет вычислить координату точки . |
||||||||||||||||||||||||||||||
|
|
Рассмотрим частный случай, когда точка является серединой от- |
||||||||||||||||||||||||||||||
|
|
̅̅̅̅̅̅̅̅ |
1 = 2 и = 1. Формулы нахождения координат |
|||||||||||||||||||||||||||||
резка 1 2. Тогда |
||||||||||||||||||||||||||||||||
середины отрезка принимают вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
= |
1+ 2 |
, = |
1+ 2 |
. |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, координаты середины отрезка равны полусумме со- |
|||||||||||||||||||||||||||||||||
ответствующих координат его концов. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
Пример 2.11. Точки (3; 7), (−4; −7), |
(5; 11) лежат на одной |
||||||||||||||||||||||||||||||||
прямой. Определить, в каком отношении точка |
|
|
|
̅̅̅̅ |
|||||||||||||||||||||||||||||||
делит отрезок С. |
|||||||||||||||||||||||||||||||||||
|
|
Решение. |
Для нахождения используем формулу = |
− 1 |
. Здесь |
||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3−(−4) |
|
|
7 |
|
|
|
2 |
|
|
|||
= 3, |
= −4, |
|
= 5. Тогда: = |
= |
. |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5−3 |
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Ответ: |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Пример 2.12. Даны две точки 1(2; |
|
5) и 2(3; −7). Найти коорди- |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̅̅̅̅̅̅̅̅ |
|
в отношении = |
1 |
. |
|
|
|
|
|||
наты точки , которая делит отрезок 1 2 |
|
3 |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
Здесь 1 = 2, |
|
2 = 3, 1 = 5, 2 = −7. Найдём абсциссу |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
точки : = |
1+ 2 |
= |
2+3∙3 |
= |
9 |
|
. Найдём ординату точки : = |
1+ 2 |
= |
||||||||||||||||||||||||||
|
|
|
1 |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1+ |
1+ |
3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
1+ |
||||||||||
|
5+1∙(−7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
|
3 |
|
|
= 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
( |
9 |
|
; 2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Пример 2.13. Даны две точки 1(−8; 1) и 2(2; −5). Найти коор- |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̅̅̅̅̅̅̅̅ |
|
|
|
|
|
|
|
|
|
|
|||||||||
динаты середины отрезка 1 |
2. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
Решение. Здесь 1 = −8, 2 = 2, 1 = 1, 2 = −5. Найдём абсциссу |
|||||||||||||||||||||||||||||||||
середины отрезка: |
= |
1+ 2 |
= |
−8+2 |
= −3. |
Найдём ординату середины от- |
|||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
резка:
= 1+2 2 = 1−25 = −2.
Ответ: (−3; −2).
Пример 2.14. Даны вершины треугольника (2; −5), (1; −2),(4; 7). Найти точку пересечения биссектрисы его внутреннего угла при вершине со стороной .
Решение. Обозначим точку пересечения биссектрисы со сторонойчерез (рис. 2.16).
|
|
|
|
|

Рис. 2.16. Треугольник и биссектриса (к Примеру 2.14)
35
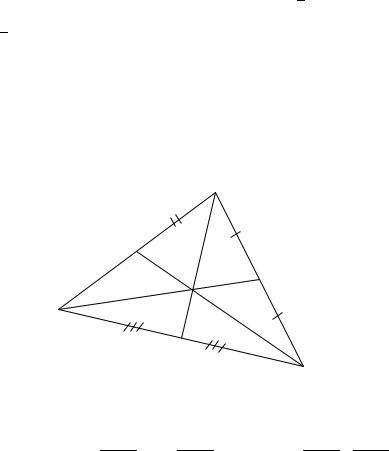
Известно, что биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторо-
нам. Тогда можно записать соотношение: |
| | |
|
= |
|
|
| | |
. |
|
||||||||||||||||||||||||||||||||||||||||
| | |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | |
|||||||||
|
|
По формуле расстояния между двумя точками: |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
| |
|
|
√ |
( |
|
|
|
|
|
) |
2 |
|
|
(−2 |
|
|
( |
|
|
|
) |
) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
= |
1 − 2 |
+ |
− |
−5 |
= √10, |
||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
| |
|
| |
|
|
√ |
( |
|
|
|
|
|
) |
2 |
|
|
|
|
( |
|
|
|
|
) |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
= |
4 − 1 |
+ |
(7 − |
−2 |
) = √90 = 3√10. |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
| | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
√10 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̅̅̅̅ |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Тогда | | = |
|
|
|
|
= 3 |
, то есть точка делит отрезок в отношении |
||||||||||||||||||||||||||||||||||||||||
1 |
3√10 |
|
||||||||||||||||||||||||||||||||||||||||||||||
= |
. Найдём координаты точки : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
= |
1+ 2 |
= |
|
2+3∙4 |
= |
5 |
, = |
1+ 2 |
= |
|
−5+3∙7 |
|
= −2. |
|||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
1 |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1+ |
|
|
|
1+ |
3 |
|
|
2 |
|
|
|
|
1+ |
|
|
|
|
1+ |
3 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Точка пересечения биссектрисы и стороны : (52 ; −2).
Ответ: (52 ; −2).
Пример 2.15. Даны вершины однородной треугольной пластины
1( 1; 1), 2( 2; 2), 3( 3; 3). Определить координаты её центра масс. Указание. Центр масс находится в точке пересечения медиан.
Решение. Обозначим точку пересечения медиан через . Точку пересечения медианы, проведённой из вершины 1, с противоположной стороной обозначим через (рис. 2.17).
2
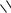 1
1
3
Рис. 2.17. Нахождение центра масс треугольной пластины (к Примеру 2.15)
Учитывая, формулы нахождения координат середины отрезка, находим координаты точки : = 2+2 3, = 2+2 3. Имеем: ( 2+2 3 ; 2+2 3).
Известно, что медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2: 1, считая от вершины, то есть точка
делит медиану 1 в отношении 2: 1, считая от точки 1. С учётом этого, |
||||||||||||
= |
| 1 | |
= 2. Далее находим точку : |
|
|
|
|
||||||
| | |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+2∙ 2+ 3 |
|
+ + |
+2∙ 2+ 3 |
|
+ + |
|||
|
|
|
1 |
2 |
|
1 |
2 |
|
||||
|
= |
|
= |
1 2 3 |
, = |
|
= |
1 2 3 |
. |
|||
|
|
1+2 |
|
1+2 |
|
3 |
||||||
|
|
|
|
3 |
|
|
|
|
||||
Получаем следующий центр масс однородной треугольной пластины:
36
( |
1+ 2+ 3 |
; |
1+ 2+ 3 |
). |
|
|||
|
|
|
||||||
3 |
|
|
3 |
|
|
|
|
|
Ответ: ( |
1+ 2+ 3 |
; |
1+ 2+ 3 |
). |
||||
|
3 |
|||||||
|
|
|
|
3 |
|
|
||
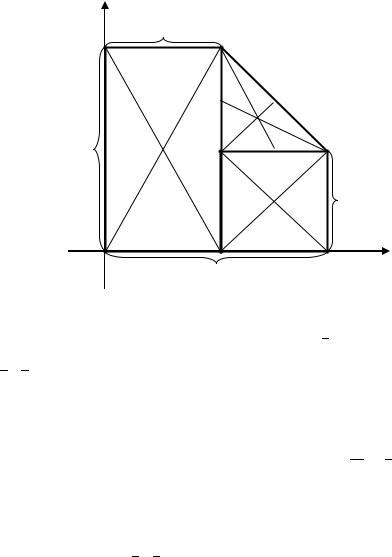
Пример 2.16. Однородная пластинка имеет форму квадрата со стороной, равной 2, от которого отрезан треугольник; прямая разреза соединяет середины двух смежных сторон, оси координат направлены по рёбрам пластины. Определить центр масс пластины.
Указание. Если однородную пластину разбить на две части и найти центр масс каждой из них, то центр масс исходной пластины находится в точке, которая делит расстояние между центрами масс каждой из частей в отношении, обратном отношению их площадей. Центр масс треугольника находится в точке пересечения его медиан. Центр масс прямоугольника находится в точке пересечения его диагоналей.
Решение. Разобьём пластину на три фигуры: прямоугольник, квадрат и треугольник. Центр масс прямоугольника обозначим 1, квадрата – 2, треугольника – 3 (рис. 2.18).
1
2 |
1 |
3 |
|
|
|
||
|
|
2 |
1 |
|
|
2 |
|
|
|
|
Рис. 2.18. Нахождение центра масс пластины (к Примеру 2.16)
По чертежу центр масс прямоугольника: 1 (12 ; 1), центр масс квад-
рата: 2 (32 ; 12). Сначала найдём центр масс пластины, состоящей из прямо-
угольника и квадрата. Для этого найдём их площади: 1 = 2, 2 = 1 соответственно. Тогда, согласно указанию к задаче, центр масс пластины, состоящей из прямоугольника и квадрата, находится в точке, которая делит
расстояние между точками 1 и 2 в отношении 1 = 2 = 1. Тогда центр
1 2
масс пластины, состоящей из прямоугольника и квадрата:
|
|
1 |
1 3 |
|
|
|
|
|
|
1 1 |
|
|
|
||
= |
1+ 1 2 |
= 2+21∙2 |
= |
5 |
|
, = |
1+ 1 2 |
= |
1+2∙2 |
= |
5 |
. |
|||
1+ 1 |
|
|
1 |
|
|||||||||||
|
1+ |
2 |
6 |
|
1+ 1 |
1+ |
2 |
6 |
|||||||
Получаем точку ′ (56 ; 56) – центр масс пластины, состоящей из прямоугольника и квадрата.
37
Далее найдём центр масс треугольника, используя результат Примера 2.15. Обозначим вершины треугольника через , , и запишем их координаты: (1; 2), (2; 1), (1; 1). Тогда координаты центра масс треугольника:
= |
1+ 2+ 3 |
= |
1+2+1 |
= |
4 |
, = |
1+ 2+ 3 |
= |
2+1+1 |
= |
4 |
. |
|
|
|
|
|
|
|||||||
3 |
3 |
3 |
3 |
3 |
3 |
|||||||
Получили точку 3 (43 ; 43) – центр масс треугольника.
Далее для нахождения центра масс исходной пластины нам понадобится площадь треугольника: 3 = 12.
Находим центр масс исходной пластины, учитывая, что он находится в точке, которая, согласно указанию к задаче, делит расстояние между точ-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
ками ′ и в отношении |
2 |
= |
= |
2 |
= |
: |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
1+ 2 |
2+1 |
6 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
5 |
1 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 4 |
|
|
|
|
||||||
′ = |
1+ 2 2 |
= 6+61∙3 |
= |
|
19 |
, ′ = |
|
1+ 2 2 |
= |
6+61∙3 |
= |
19 |
. |
|||||||||||||||||
|
|
21 |
|
21 |
||||||||||||||||||||||||||
|
1+ 2 |
1+ |
6 |
|
|
|
|
1+ 2 |
|
|
|
|
1+ |
6 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, получили точку |
( |
19 |
; |
19 |
) |
– |
центр масс исходной |
|||||||||||||||||||||||
|
21 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|||||
пластины. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: ( |
19 |
; |
19 |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
21 |
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2.5. Вычисление площади треугольника через координаты его вершин
Пусть 1( 1; 1), 2( 2; 2) и 3( 3; 3) – три данные точки, не лежащие на одной прямой. Вычислим площадь треугольника 1 2 3 че-
рез координаты его вершин. Обозначим через угол между отрезками
̅̅̅̅̅̅̅̅ |
̅̅̅̅̅̅̅̅ |
|
|
̅̅̅̅̅̅̅̅ |
1 2 |
и 1 3, через 1 |
обозначим полярный угол отрезка 1 2, через 2 |
||
|
|
̅̅̅̅̅̅̅̅ |
|
|
обозначим полярный угол отрезка 1 3. Рассмотрим два случая: когда |
||||
|
|
̅̅̅̅̅̅̅̅ |
̅̅̅̅̅̅̅̅ |
положителен и отрицате- |
наименьший угол между отрезками 1 2 |
и 1 3 |
|||
лен (рис. 2.19, рис. 2.20).
3
|
2 |
|
2 |
|
|
|
1 |
|
1 |
|
|
Рис. 2.19. Треугольник 1 2 3, когда наименьший угол |
||
̅̅̅̅̅̅̅̅ |
̅̅̅̅̅̅̅̅ |
положителен |
между отрезками 1 2 |
и 1 3 |
|
38 |
|
|

2
|
|
|
3 |
|
|
1 |
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
Рис. 2.20. Треугольник 1 2 |
3, когда наименьший угол |
||
̅̅̅̅̅̅̅̅ |
̅̅̅̅̅̅̅̅ |
отрицателен |
|
между отрезками 1 2 |
и 1 3 |
||
Найдём площадь треугольника 1 2 3. Площадь треугольника возьмём как половину произведения двух сторон треугольника на синус уг-
ла между ними: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
1 |
| |
| ∙ |
| | sin . |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
∆ |
2 |
1 2 |
|
1 3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
̅̅̅̅̅̅̅̅ |
̅̅̅̅̅̅̅̅ |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Если наименьший угол между отрезками 1 2 |
и 1 3 положителен |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̅̅̅̅̅̅̅̅ |
|
(рис. 2.19), то = 2 − 1. Если наименьший угол между отрезками 1 |
2 |
||||||||||||||||||||
̅̅̅̅̅̅̅̅ |
отрицателен (рис. 2.20), то = 1 − 2. Таким образом, = |
|
|||||||||||||||||||
и 1 3 |
|
||||||||||||||||||||
= ±( 2 − 1). Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
= |
1 |
| |
| ∙ |
| | sin = |
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
∆ |
2 |
1 2 |
|
1 |
3 |
|
|
|
|
|
|
||||||||
|
1 |
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
= ± |
| |
| ∙ | |
| sin( |
|
− ) |
= |
|
|
|
|
|||||||||||
|
2 |
|
|
|
|
||||||||||||||||
2 |
1 |
2 |
|
1 |
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|||||
= ± |
1 |
| |
| ∙ | |
|(sin |
|
cos |
− cos |
sin ). |
|
|
|||||||||||
|
2 |
|
|
||||||||||||||||||
2 |
1 |
2 |
|
1 |
2 |
|
|
|
1 |
|
2 |
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Учитывая формулы нахождения проекций направленного отрезка на |
|||||||||||||||||||
координатные оси через длину и полярный угол отрезка, получаем: |
|
||||||||||||||||||||
|
|
|
̅̅̅̅̅̅̅̅ |
= |
|
|
|
|
|
|
|
|
|
|
̅̅̅̅̅̅̅̅ |
= | 1 2| sin 1, |
|
||||
|
|
пр 1 |
2 |
|
| 1 2| cos 1, пр 1 2 |
|
|||||||||||||||
|
|
|
̅̅̅̅̅̅̅̅ |
= |
|
|
|
|
|
|
|
|
|
|
̅̅̅̅̅̅̅̅ |
= | 1 3| sin 2. |
|
||||
|
|
пр 1 |
3 |
|
| 1 3| cos 2, пр 1 3 |
|
|||||||||||||||
=± 12
=± 12
=± 12
Тогда площадь треугольника: |
|
|
|
|
|
||||||||||
|
|
|
|
|
= ± |
1 |
|
| |
| ∙ | |
|(sin |
cos − cos |
sin ) = |
|||
|
|
|
|
|
|||||||||||
∆ |
|
|
2 |
1 2 |
1 3 |
|
2 |
1 |
2 |
1 |
|||||
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
||||
(| 1 |
2 |
|
| ∙ | 1 3 | sin 2 cos 1 − | 1 |
2 | ∙ | 1 3 | cos 2 sin 1) = |
|||||||||||
(| 1 |
2 |
|
| cos 1 |
∙ | 1 3 | sin 2 |
− | 1 |
2 | sin 1 |
∙ | 1 3| cos 2) = |
||||||||
|
|
̅̅̅̅̅̅̅̅ |
|
|
|
̅̅̅̅̅̅̅̅ |
̅̅̅̅̅̅̅̅ |
|
̅̅̅̅̅̅̅̅ |
|
|
||||
(пр 1 |
2 |
∙ пр 1 3 |
− пр 1 |
2 ∙ пр |
1 3). |
|
|
||||||||
Учитывая формулы нахождения проекций направленного отрезка на
координатные оси через координаты концов отрезка, получаем:
∆ 1 2 3 = ± 12 [( 2 − 1)( 3 − 1) − ( 2 − 1)( 3 − 1)].
С учётом понятия определителя второго порядка формулу площади треугольника можно записать в виде:
39
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
± |
|
|
|
|
|
= |
1 |
|
| 2 − 1 |
|
2 − 1 |
|. |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 − 1 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
|
|
|
|
|
|
3 − 1 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Если три точки 1( 1; 1), 2( 2; 2) и 3( 3; 3) лежат на одной |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
прямой, то площадь треугольника 1 2 3 |
|
равна нулю. Формула площади |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
принимает вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
± |
1 |
|
[( − )( − ) |
− ( − )( − )] = 0. |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
1 |
3 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
3 |
1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Отсюда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 2 − 1)( 3 − 1) − ( 2 |
|
− 1)( 3 − 1) = 0 |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2− 1 |
= |
|
2− 1 |
. |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
− |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
|
|
3 |
|
|
1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Полученная формула связывает координаты трёх точек, лежащих на |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
одной прямой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
Пример 2.17. Даны три точки 1(−5; −2), |
2(−1; 4) и 3(3; 2). |
||||||||||||||||||||||||||||||||||||||||||||||||||||
Найти площадь треугольника 1 2 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Решение. По формуле площади треугольника получаем: |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
± |
|
|
|
|
|
|
|
|
|
= |
1 |
| |
2 − 1 |
2 |
|
− 1 |
| |
= |
1 |
| |
−1 − (−5) 4 − (−2) |
| = |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 − 1 |
3 − 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
∆ |
|
|
2 |
|
|
|
|
|
|
|
2 3 − (−5) 2 − (−2) |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
|
1 |
|4 |
|
6| = |
1 |
∙ (−32) = −16. Отсюда |
|
|
|
|
|
|
|
|
= 16. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
2 |
8 |
|
4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
3 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
Ответ: 16. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
Пример 2.18. |
|
Выяснить, |
лежат |
|
ли |
|
|
точки |
1(2; −3), 2(6; 5) и |
||||||||||||||||||||||||||||||||||||||||||||
3(−1; −9) на одной прямой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
Решение. Воспользуемся условием, при котором три точки лежат на |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
одной прямой: |
2− 1 |
= |
|
2− 1 |
|
. Подставляем координаты данных точек: |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
− |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
1 |
|
|
|
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
6−2 |
= |
|
|
5−(−3) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
−1−2 |
|
|
|
−9−(−3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
Отсюда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
4 |
= |
|
8 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
−3 |
|
−6 |
|
|
|
4 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
То есть − |
|
= − |
и точки лежат на одной прямой. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
Ответ: точки лежат на одной прямой. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Пример 2.19. Известны координаты |
|
двух |
вершин треугольника |
||||||||||||||||||||||||||||||||||||||||||||||||||
(2; 1) и (3; −2), |
|
|
|
а третья вершина лежит на оси . Площадь тре- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
угольника равна 4. Найти координаты вершины . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Решение. Обозначим абсциссу точки через , ордината этой точки |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
равна 0: ( ; 0). По формуле площади треугольника получаем: |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
± |
|
|
|
= |
1 |
| 2 |
− 1 |
|
|
|
2 |
− 1| = |
1 |
|3 − 2 −2 − 1| = |
1 |
| 1 |
−3| = |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
∆ |
|
|
2 |
3 |
− 1 |
|
|
|
3 − 1 |
|
|
|
2 − 2 |
|
0 − 1 |
|
2 − 2 −1 |
||||||||||||||||||||||||||||||||||
= |
1 |
(−1 + 3( − 2)) |
= |
1 |
(−7 + 3 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
По условию площадь треугольника равна 4, поэтому получаем сле- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
дующее уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
1 |
(−7 + 3 ) = ±4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
1 |
(−7 + 3 ) = 4 или |
|
1 |
(−7 + 3 ) = −4. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
40
