3. Непрерывные детерминированные модели Непрерывные модели динамических систем

Математические методы описания и анализа физических, механических, экологических, экономических и других динамических систем имеют разную историю, традиции и разный уровень развития. И хотя современные исследования связаны с понятием динамической системы в более широком смысле (включающем объекты, описываемые общими, как правило, стохастическими функциональными соотношениями), классические динамические системы, полученные на базе теории обыкновенных дифференциальных уравнений, продолжают оставаться основным инструментом решения многих практических задач [2,12]. Это объясняется, во-первых, наличием хорошо развитого аналитического аппарата и численных методов решения обыкновенных дифференциальных уравнений; во-вторых, наличием общедоступных качественных методов исследования решений обыкновенных дифференциальных уравнений, в частности методов оценки устойчивости, анализа поведения решений в окрестности особых точек и их асимптотического поведения и др.; и, в-третьих, прозрачностью и естественностью дифференциального уравнения как математической модели для описания процессов перехода реальных объектов из одного состояния в другое под действием внешних и внутренних причин.

Упомянутые обстоятельства приводят к тому, что системы, описываемые обыкновенными дифференциальными уравнениями, оказываются в методическом отношении весьма удобным материалом для первоначального ознакомления с общими понятиями, математическим аппаратом и методами моделирования динамических систем.

Систему обыкновенных дифференциальных уравнений, полученную в результате исследования какого-либо явления или процесса, называют непрерывной модельюэтого явления или процесса, поскольку все переменные этой модели являются непрерывными функциями времени. Такого рода модели технических систем в большинстве своем могут быть отнесены к классуаксиоматических, то есть полученных на основе законов той области науки, с которой связана природа изучаемой задачи. Так, например, в механике это могут быть законы Ньютона, в теории электрических цепей - законы Кирхгофа, в теории кинетики химических реакций - законы действия масс и т.д. Аксиоматические модели обладают достаточной точностью, чтобы быть использованными для получения как качественных, так и количественных характеристик моделируемых объектов (пример 3.1).

Для других систем, например производственных, экономических и экологических, для которых до сих пор не существует удовлетворительной системы постулатов математического описания взаимодействия элементов, дифференциальные модели строят исходя из интуитивно оправданных, не противоречащих опыту предположений относительно вида функции взаимосвязи фазовых переменных и темпов их изменения. Количественные значения параметров функциональных зависимостей в этом случае могут быть определены на основе экспериментальных данных, но чаще такие модели предназначаются для качественного исследования моделируемых систем (примеры 3.2, 3.3).

Пример 3.1.Механическая система. Простейшим примером аксиоматической модели является модель системы, состоящей из тела, которое совершает горизонтальные движения в вакууме под действием двух пружин (рис.3.1). Такая система является консервативной, т.е. системой, рассеянием энергии в которой можно пренебречь. Еслиобозначает смещение тела массойиз состояния равновесия, а сила, с которой пружины действуют на тело (восстанавливающая сила), пропорциональна смещению, то уравнение движения имеет вид

,

Рис.3.1.Простейшая механическая система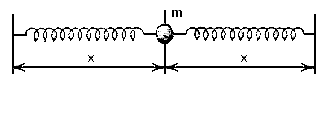

Пружины этого типа называются линейными, так как их восстанавливающая сила является линейной функцией. Если восстанавливающая сила f является произвольной функцией, такой чтоf(0)=0, то получим специальный случайнелинейной консервативной системы, которая описывается уравнением

.

Пример 3.2.Эффективность рекламы. Предположим, что торговыми учреждениями реализуется продукция, о которой в момент временииз числа потенциальных покупателейзнает лишьпокупателей. Предположим далее, что для ускорения сбыта продукциибыли даны рекламные объявления по радио и телевидению.

Последующая информация о продукции распространяется среди покупателей посредством общения друг с другом. С большой степенью достоверности можно считать, что после рекламных объявлений скорость изменения числа знающих о продукции пропорциональна как числу знающих о товаре покупателей, так и числу покупателей, о нем еще не знающих.

Если условиться, что время отсчитывается после рекламных объявлений, когда о товаре узнало человек, то приходим к дифференциальному уравнению

с начальными условиями . В полученном уравнении коэффициент- это положительный коэффициент пропорциональности.

Пример 3.3. Модели в экологии. Экология изучает взаимоотношение человека и вообще живых организмов с окружающей средой. Основным объектом экологии является эволюция популяций. Пусть- число особей в популяции в момент времени. Тогда если- число особей в популяции, рождающихся в единицу времени, а- число особей, умирающих в единицу времени, то с достаточным основанием можно утверждать, что скорость изменениясо временем задается формулой

.

Задача теперь состоит в том, чтобы описать зависимость иот. Простейшим случаем является ситуация, когдаA=ax, B=bx , гдеи- коэффициенты рождаемости и смертности особей в единицу времени соответственно. С учетом равенств дифференциальное уравнение перепишется в виде

.

Хотя приведенная модель является упрощенной, она все-таки в ряде случаев соответствует действительности. Практически же все модели, которые описывают реальные явления и процессы, нелинейны, и вместо линейного дифференциальнoгo уравнения следует рассматривать уравнение вида

,

где - нелинейная функция, например вида

, где.

Если рассматривается несколько сосуществующих видов, например, больших и малых рыб, где малые рыбы являются кормом для больших, то, составляя дифференциальные уравнения для каждого вида, получим систему дифференциальных уравнений

Рассмотрим, например, двухвидовую модель «хищник - жертва», которая впервые была построена Вольтерра для объяснения колебаний рыбных уловов в Адриатическом море, имеющих один и тот же период, но отличающихся по фазе.

Пусть - число больших рыб-хищников, которые питаются малыми рыбами-жертвами, число которых обозначим через. Модель, построенная Вольтерра, имеет вид

где - положительные константы.

В первом уравнении для больших рыб слагаемое выражает зависимость прироста больших рыб от численности малых рыб. Во втором уравнении слагаемоевыражает уменьшение числа малых особей в зависимости от численности больших. Согласно модели число рыб-хищников будет расти до тех пор, пока у них будет достаточно пищи, т. е. малых рыб-жертв, но в конце концов наступит ситуация, когда корма не будет хватать и в результате число больших рыб начнет уменьшаться. Это приведет к тому, что с некоторого момента число малых рыб снова начнет увеличиваться. Это будет способствовать новому росту числа больших особей, и цикл снова повторится.