Фазовые портреты простых канонических систем

(a) Различные действительные собственные значения

Система уравнений имеет вид

Решением системы является y₁ =; y₂ =,откуда получаем. Возможны два варианта:

(а.1) Корни ₁ и ₂ противоположного знака.

П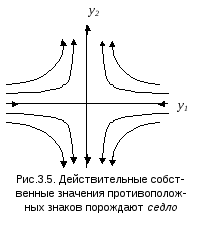олучается семействогипербол, имеющих асимптотами осиу1 иу2, которые так же являются траекториями. Направления, по которым траектории проходят через стационарную точку, можно определить непосредственно из решений приt,изменяющемся от0до. Суммарный фазовый портрет такой системы называетсяседлом.

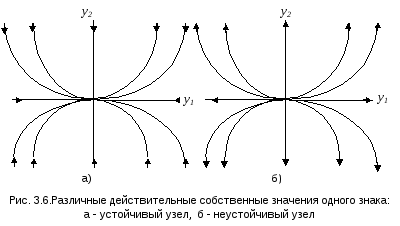
(а.2) Корни ₁ и ₂ одного знака.

Траектории в этом случае образуют семейство степенных функций, причем каждая траектория входит в точку покоя или выходит из нее (в зависимости от знака корней) с различных направлений. Совокупная картина фазовых траекторий называется в этом случае узлом устойчивым илинеустойчивым (рис.3.6).

(в) Действительные кратные собственные значения.

В этом случае имеем систему уравнений

имеющую решение. Откуда получаемy₂=cy₁, т.е. интегральными линиями служат все прямые, проходящие через начало координат. Этозвездообразный(звездный) узел.

(c)Действительные кратные значения.

В этом случае система уравнений принимает вид:

Получаем узел с одним направлением входа устойчивый при ₀ < 0 и неустойчивый при₀ > 0. Такой фазовый портрет называетсявырожденным узлом. Узлы такого вида представляют собой точки с координатами (2n,0), где n=0,1,... механической системы с трением, фазовый портрет которой приведен на рис.3.4,b.

(d) Комплексные собственные значения.

Система уравнений имеет вид

Выполним замену переменных:

Переходя в плоскости y₁ , y₂ к полярным координатам, получим систему уравнений

имеющую следующее решение:

Последнее уравнение задает логарифмические спирали, выходящие (или входящие) из начала координат (точки покоя). Направление движения по траекториям приt,изменяющемся от 0 до, определяется из решения системы уравнений. При < 0имеем устойчивый фокус, а при > 0-неустойчивый. При =0получим = с, т.е. в плоскостих,уполучается семейство подобных окружностей с общими осями симметрии. Фазовый портрет в этом случае называетсяцентром.

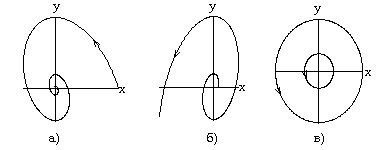
Рис.3.8. Комплексные собственные значения порождают:

а - неустойчивый фокус, >0

б - устойчивый фокус, <0

в - центр, =0

Фазовый портрет простой линейной системы

Фазовый портрет простой линейной системы можно получить из фазового портрета канонической системы с помощью преобразованияx=My, где являются координатами точкиx относительно базиса{m₁, m₂}, составленного из столбцов матрицыМ. Отсюда оси - это прямые, проходящие через начало координат на плоскости и имеющие направление векторовm₁, m₂. Влияние линейных преобразований вида x=My на фазовый портрет канонической системы

Рис.3.10. Влияние линейных преобразований на фазовый портрет

показано на рис.3.9, где (а) - фазовый портрет исходной канонической системы, а (б) - фазовый портрет преобразованной системы при матрице преобразований.

Рис.3.9.Влияние линейных преобразований на фазовый портрет:

а – каноническая система,

б – преобразованная система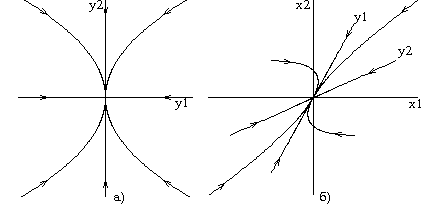

Теперь мы можем найти решение для любой линейной системы общего вида, если определим соответствующую ей каноническую систему и применим линейное преобразование координат.