Качественная эквивалентность

Две системы обыкновенных дифференциальных уравнений называются качественно (топологически) эквивалентными, если существует непрерывное взаимооднозначное преобразование, которое переводит фазовый портрет одной системы в фазовый портрет другой, так что сохраняется ориентация траекторий. Различных качественных типов фазовых портретов для линейных систем всего четыре: устойчивые, центр, седло, неустойчивые.

Непростые канонические системы

Линейная система называется непростой канонической, еслиA- сингулярная матрица, т.е.detA = 0, и, следовательно, хотя бы одно из собственных значенийA равно нулю. Отсюда следует, что существуют нетривиальные решения уравненияAx = 0и что кромеx=0система имеет и другие неподвижные точки. Для линейных систем на плоскости существует только две такие возможности: рангAравен 1, A- нулевая матрица.

На рис.3.10 показаны два примера , когда ранг А равен единице:

(a)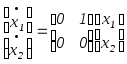, (б) .

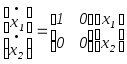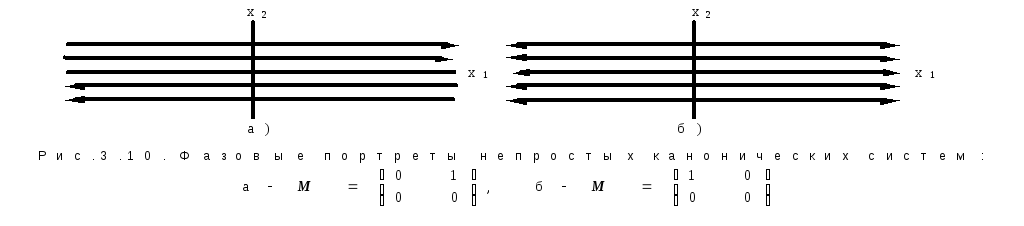
В примере (а) все точки оси x₁ являются неподвижными точками системы, а в случае (б) стационарные точки системы полностью заполняют ось x₂. Во втором из возможных вариантов, когда матрицаА нулевая (A = 0),все точки плоскостиx₁,x₂ являются неподвижными.

Выводы

Всё сказанное ранее относительно простых и непростых канонических систем второго порядка можно отобразить в виде следующей схемы, приведенной на рис.3.11.

Каждому типу фазового портрета соответствует некоторое множество точек на плоскостиtrA-detA. Каждой точке этой плоскости соответствует определённая пара собственных значений матрицыAи, следовательно, определённая каноническая система. Рис.3.11 иллюстрирует зависимость фазовых портретов и структуры корней характеристического уравнения от параметров системы обыкновенных дифференциальных уравнений, выраженных через след матрицы коэффициентов и ее определитель.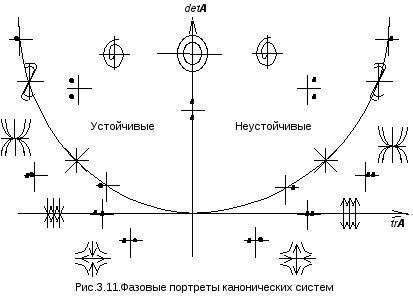

Нелинейные системы Глобальные и локальные фазовые портреты

Математическая модель нелинейной системы может быть представлена системой нелинейных дифференциальных уравнений где f(x)- нелинейная функция,x S  Rⁿ, n- порядок системы уравнений.

Рис.3.12.Примеры фазовых портретов нелинейных систем имеющих три (a) и две (b) стационарные точки

В отличие от линейных нелинейные системы могут иметь любое количество стационарных точек, и поэтому их фазовые портреты отличаются бесконечным разнообразием. На рис.3.12 приведены примеры фазовых портретов нелинейных систем второго порядка.

Ф

Рис.3.15 Фазовый портрет нелинейной системы, содержащей предельный цикл.

азовый портрет нелинейной системыпостроенный на всем фазовом пространствеS,называетсяглобальным.С увеличением размерности фазового пространства построение глобального фазового портрета и его исследование становятся все более сложной задачей. Исходя из этого, часто исследуют фазовый портрет только в определенной области фазового пространства, например в окрестности состояния равновесия или вблизи замкнутой траектории.

Рис.3.12.Фазовые портреты нелинейных систем:

а – имеет три стационарные точки, б – имеет две стационарные точки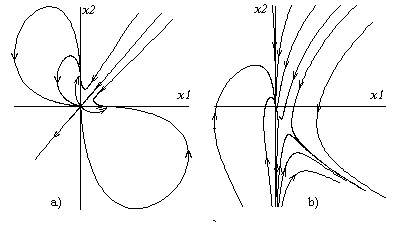

Локальнымфазовым портретом называется часть глобального фазового портрета системы, находящаяся в окрестности стационарной точки. Следует заметить, что совпадение локальных фазовых портретов в неподвижных точках не гарантирует эквивалентности глобального поведения.

На рис.3.14 показано ещё одно глобальное свойство фазовых портретов, которое не вытекает из исследования неподвижных точек. Изолированная замкнутая орбита вокруг одной из неподвижных точек называется предельным циклом. Нахождение предельных циклов требует глобального подхода. Таким образом, рассмотрение нелинейных систем требует техники, пригодной для исследования как локального, так и глобального поведения.