Многоканальные смо с взаимопомощью

В системах ПВО при появлении цели-заявки все приборы слежения и уничтожения могут работать по одной цели, увеличивая интенсивность обслуживания. С появлением второй цели-заявки часть приборов переключается на эту цель и т.д.

В системах обслуживания, организованных по такому принципу, интенсивность обслуживания увеличивается пропорционально числу обслуживающих устройств: , где - количество приборов; - интенсивность обслуживания одним прибором.

Можно показать, что для марковских систем неважно, как распределяются каналы между заявками при условии участия всех приборов в обслуживании. Таким образом, систему, имеющую каналов обслуживания, мы можем эквивалентировать системой, имеющей одно обслуживающее устройство с интенсивностьюS, при этом в системе может находиться от 0 до заявок одновременно.

При поступлении заявки в систему, в которой , заявка получит отказ. Если канал освободился от обслуживания, то он подключается к обслуживанию имеющихся в системе заявок.

Граф переходов системы с взаимопомощью показан на рис.4.11.

С помощью этого графа составим систему дифференциальных уравнений:

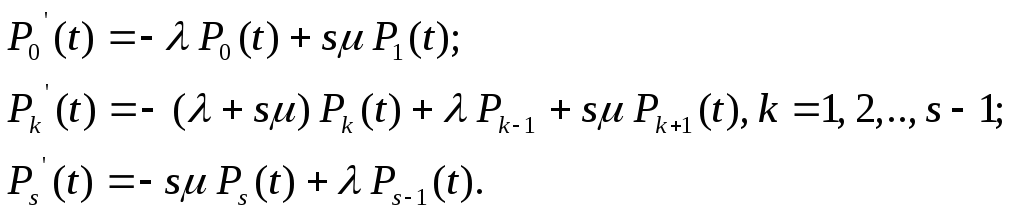Уравнения стационарного режима имеют вид

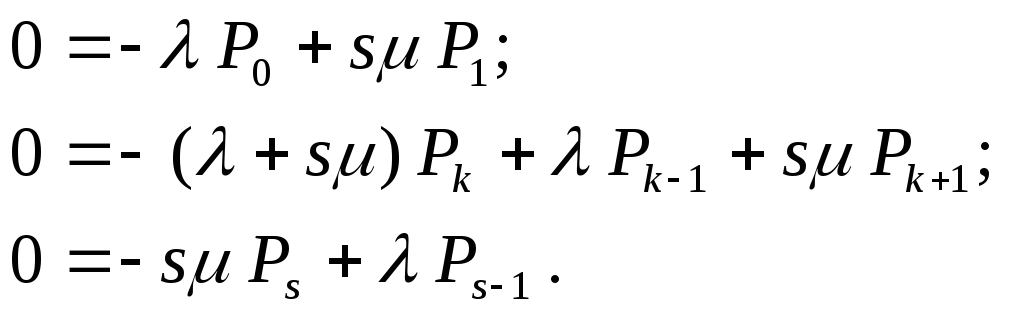
Из последних уравнений получаем .

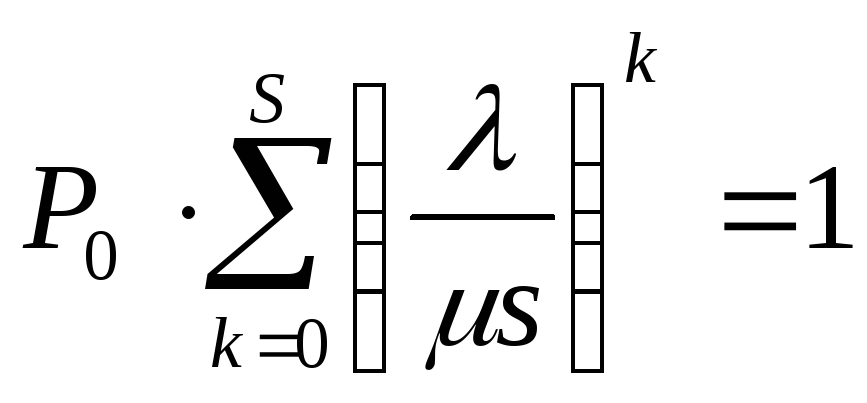Для определения привлекаем соотношение. Откуда следует, чтои далее

Окончательно

Среднее число заявок, находящихся в системе,

По этим формулам определяются и другие характеристики СМО.

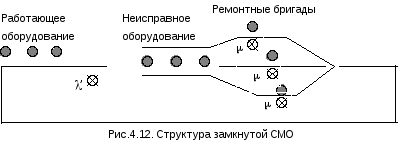
Замкнутые системы

Рассмотрим процесс восстановления единиц оборудования ремонтными бригадами. Пусть .

Предположим, что время безотказной работы единиц оборудования распределено по экспоненциальному закону с математическим ожиданием. Тогда интенсивность выхода из строя каждой единицы оборудования определяется соотношением .

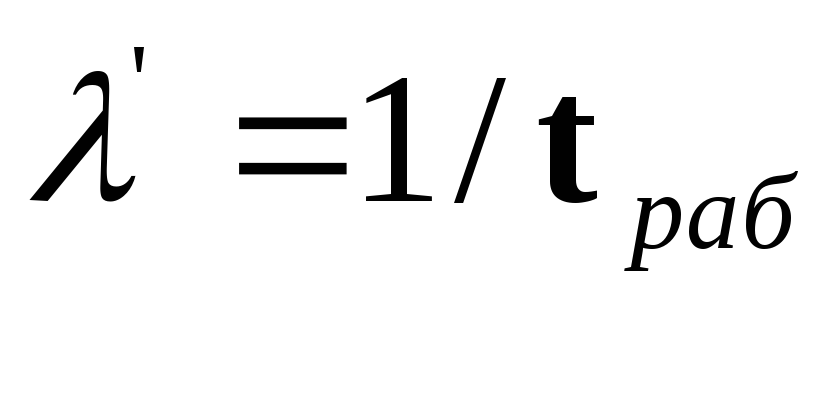Если в некоторый момент времени ремонтируется или ожидает ремонта единиц оборудования, а работают соответственно , то вероятность отказа в течение интервала равна.

При экспоненциальном времени обслуживания с параметром за интервал времениdtмогут произойти следующие переходы:

->определяется вероятностью поступления одной заявки в систему обслуживания за время : ;

->определяется вероятностью обслуживания одной заявки за время :

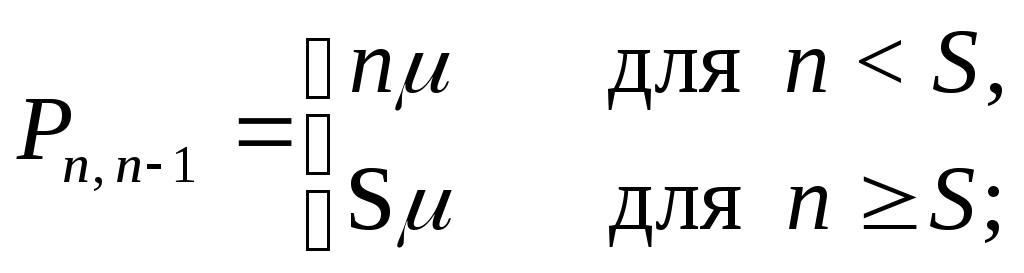
-> определяется вероятностью остаться в текущем состоянии за время :

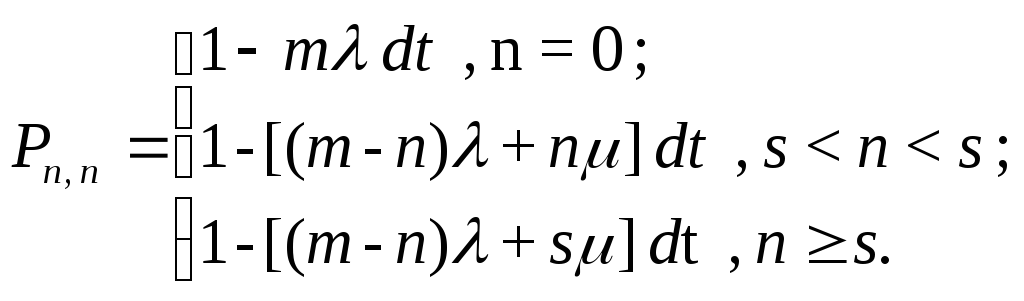
С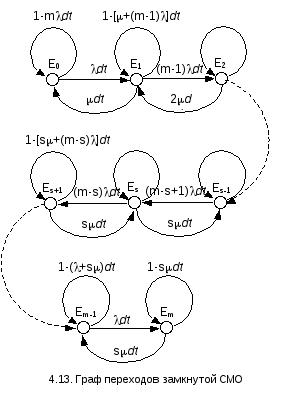оответствующий граф переходов для замкнутой СМО приведен на рис.4.13.

Уравнения состояний получаем в виде:

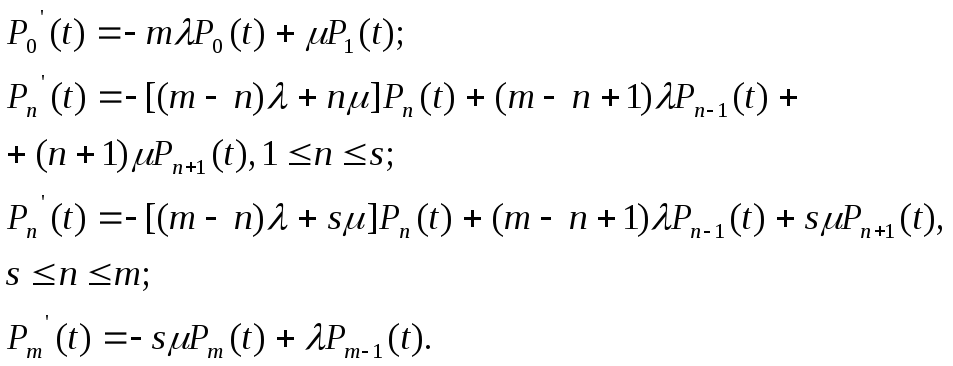
Для установившегося режима вероятности состояний определяются следующей системой:

Последовательно рассматривая уравнения, можно получить соотношения

где является коэффициентом загрузки СМО.

Комбинируя три последние формулы, получаем

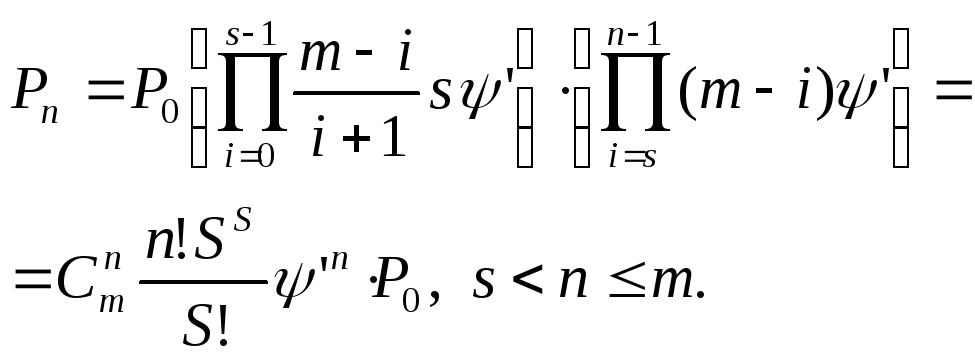
Из условия находимP₀:

.

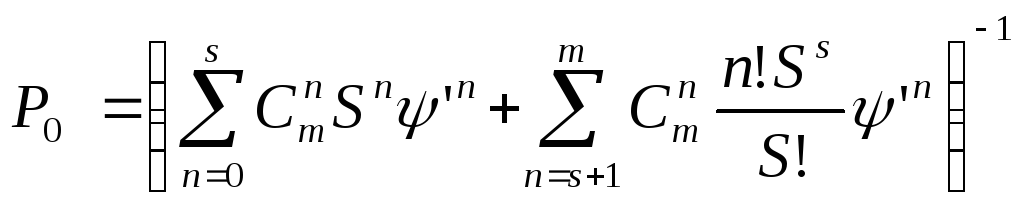Введем числовые характеристики замкнутых систем аналогично числовым характеристикам разомкнутых: - среднее число требований в очереди; () - среднее число требований, находящихся вне системы; () - среднее число занятых приборов.

Уравнения расхода для замкнутых систем можно записать в виде

,

где, напомним, - среднее число заявок в системе;- среднее время пребывания в системе; - среднее число незанятых приборов;- среднее время ожидания для одной заявки; - среднее время поступления одной заявки.

Откуда

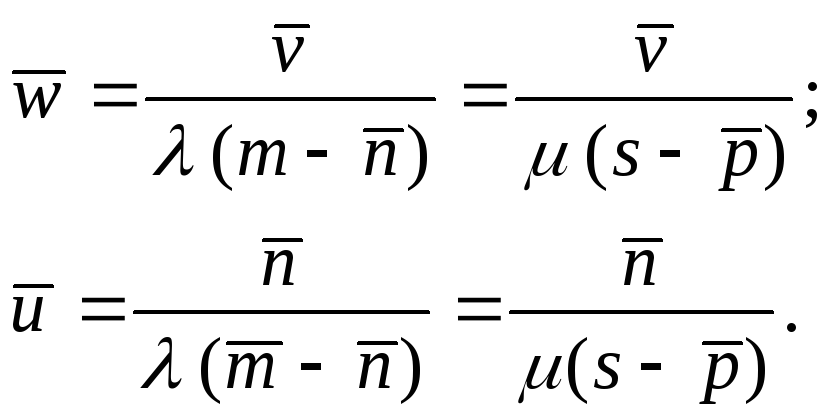
Вероятность нулевого ожидания заявки равна

.

Средняя интенсивность источника заявок в установившемся режиме.

В замкнутых системах количество заявок всегда ограничено и независимо от соотношения существует установившийся режим.

Когда коэффициент занятости прибора близок к единице, возникает явление«скученности». В этом случае основная масса заявок сосредоточивается в накопителе и устройствах обслуживания СМО и малая доля находится вне системы.