Линеаризация нелинейных систем

Рассмотрим нелинейную автономную систему

.

Пусть - неподвижная точка нелинейной системы. Будем исследовать поведение решения в окрестностях стационарного состояния. Введём вектор отклонений решения от:. Элементы вектораназываютсялокальнымикоординатами в точке.

Исходная нелинейная система уравнений в окрестности точки аппроксимируется с помощью разложения функции правых частей системы уравнений в ряд Тейлора. Сохраним члены ряда до первого порядка включительно:

Для стационарного решения имеем

и из разложения получаем

или в матричной записи

,

где , i=1,...,n, j=1,...,n.

J - матрица Якоби, причем значения всех производных берутся в точке. Полученная система уравнений представляет собой линейную систему уравнений с постоянными коэффициентами и называетсялинеаризациейнелинейной системыв точке. Для её исследования можно воспользоваться результатами анализа линейных систем.

Говорят, что стационарная точка являетсяпростойнеподвижной точкой нелинейной системы, если соответствующая линеаризованная система проста.

Следующая теорема устанавливает связь фазового портрета нелинейной системы в окрестности некоторой простой неподвижной точки с фазовым портретом ее линеаризации.

Теорема о линеаризации.Пусть нелинейная системаимеет простую неподвижную точкуx*. Тогда в окрестности этой точки фазовые портреты системы и ее линеаризации будуткачественно эквивалентны, если только неподвижная точка линеаризованной системы не являетсяцентром.

Принимая эту теорему без доказательства, отметим лишь, что особые точки типа узел, фокус и седло относят к так называемымгрубымособым точкам: их характер не меняется при малых возмущениях правых частей исходной нелинейной системы. Особая же точкацентр-негрубаяточка: характер фазовых траекторий в ее окрестности меняется уже при малых изменениях правых частей системы дифференциальных уравнений. При этом центр превращается в устойчивый или в неустойчивый фокус.

Г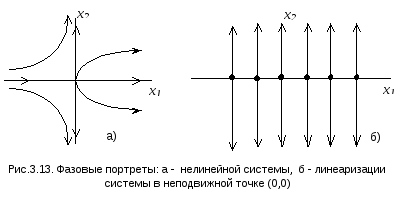оворят что неподвижная точка нелинейной системынепростая, если соответствующая точка линеаризованной системы является непростой. Фазовые портреты нелинейной системы и ее линеаризации в этом случае могут качественно отличаться. Характер локального фазового поведения определяется теперь нелинейными членами. Поэтому, в отличие от простых неподвижных точек, существует бесконечно много различных типов локальных фазовых портретов нелинейных систем в окрестности непростых неподвижных точек. На рис.3.13 приведены фазовые портреты нелинейной системыи ее линеаризациив стационарной точке этой системы (0,0).

Предельные циклы

Известно, что в случае особой точки типа центра некоторая область фазовой плоскости сплошь заполнена замкнутыми траекториями. Вместе с тем возможна и более сложная ситуация, когда имеется изолированная замкнутая траектория, т. е. траектория, в некоторой окрестности которой нет других замкнутых траекторий. Последний случай непосредственно связан с решением вопроса о существовании изолированных периодических решений. При этом интересно, что изолированные замкнутые траектории могут иметь только нелинейные дифференциальные уравнения и системы.

Изолированные периодические решения соответствуют самым разнообразным свойствам явлений и процессов, происходящих в биологии и радиофизике, в теории колебаний и астрономии, в медицине и теории конструирования приборов. Такие решения возникают при изучении дифференциальных моделей в экономике, при рассмотрении различных вопросов автоматического регулирования, самолетостроения и т. д. Здесь же мы рассмотрим как пример нелинейную дифференциальную систему

.

Чтобы решить ее, введем полярные координаты r,,гдеx=rcos, y=rsin.Тогда, продифференцировав соотношенияx2+y2=r2 и=arctg(y/x)поt, получим равенства

.

Умножая первое уравнение исходной системы на x, а второе - наyи складывая, с учетом первого находим, что

.

Если же умножить второе уравнение исходной системы на x, а первое - наyи вычесть, с учетом второго равенства получим соотношение

.

Система имеет единственную особую точку . Так как мы интересуемся сейчас только построением траекторий, то можно считать. А это означает, что система приводится к виду

,

.

Каждое из полученных уравнений системы легко интегрируется, и все семейство решений, как нетрудно видеть, задается формулами

или в старых переменных иформулами

Если теперь в первом уравнении системы положить , то получим. Эти равенства определяют замкнутую траекторию - окружность. Если, то ясно, чтоипри. Если же, тои сновапри. Это означает, что существует единственная замкнутая траектория, к которой все остальные траектории с течением времени приближаются по спиралям (рис. 3.14).

З

Рис.3.14. Фазовый портрет, содержащий замкнутую изолированную траекторию

амкнутые фазовые траектории, обладающие таким свойством, называютпредельными цикламиили, точнее,(орбитально) устойчивыми предельными циклами. Дело в том, что различают еще два типа предельных циклов. Предельный цикл называется(орбитально) неустойчивым, если все соседние к нему траектории спиралевидно от него удаляются приt.Предельный цикл называется(орбитально) полуустойчивым, если все траектории с одной стороны (например, изнутри) н

Рис.3.14.Фазовый портрет, содержащий замкнутую изолированную траекторию

аматываются на него, а с другой стороны (извне) разматываются с него приt.

Предельные циклы не всегда имеют вид окружностей, и не всегда их можно обнаружить, просто перейдя к полярным координатам. Не существует общих методов определения областей, содержащих предельные циклы, и поэтому успех зависит как от вида системы, так и от опыта исследователя.