книги из ГПНТБ / Пузырев В.А. Тонкие ферромагнитные пленки в радиотехнических цепях

только потери, определяемые сопротивлением намотанной катушки), так и от величины сопротивления нагрузки /?,,. Максимально возможное значение добротности выходного

рисунке дл я сравнения нанесены аналогичные эксперимен­ тально снятые зависимости.

Одним из в а ж н ы х параметров модуляционного устройства является угол направления управляющего

80

Ри с . 2.9

поля р. Величина (30pt зависит от соотношения H J H K , ко­ торое косвенно характеризует дисперсионные свойства пленки, обусловленные ее неоднородностями. В табл . 2.1

ниях управляющего поля, не превышающего оптимальной величины, можно получить из экспериментального графика рис. 2.10.

Эффективность модуляционного устройства м о ж н о оценить величиной отношения выходной мощности к пол­ ной мощности, подводимой к пленке на частоте несущей:

Л = ^ в ы х / (-^пл "Т~ -Рвых) .

где Рвых — выходная мощность высокочастотных коле­ баний; Р п л — мощность потерь в пленке.

На рис. 2.11 приведены экспериментально снятые за­ висимости эффективности модулятора от входной мощ-

81

/

Р и с . 2.11

ности. С определенного значения Рвх эффективность на­ чинает падать, что вызвано в основном влиянием гисте­ резиса (ростом потерь за счет частичного переключения пленки) . Пленки с меньшей величиной Gr имеют более крутой начальный участок зависимости (для оптималь ­ ного значения управляющего поля Ну).

82

В импульсном р е ж и м е в качестве управляющего (мо­ дулирующего) сигнала используется импульсное поле, которое формируется управляющей обмоткой (рис. 2.12). Ф о р м а ' в ы х о д н о г о радиоимпульса обмоточного варианта модулятора определяется в основном у п р а в л я ю щ е й цепью, так как постоянные времени лленки, входной и выходной цепей гораздо меньше постоянной времени управляющей цепи.

| импульсов

Осцилло­

граф

Р и с . 2.12

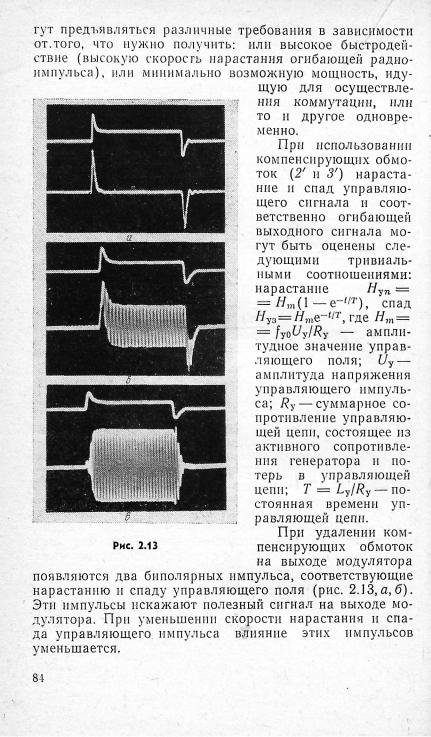
На рис. 2.13 показаны осциллограммы работы моду­

управляющей обмотке. Как можно видеть из осцилло­ грамм, форма огибающей выходного сигнала полностью определяется формой управляющего поля. Н а осцилло­ грамме рис. 2.13, а показаны управляющий (вверху) и выходной (внизу) сигналы при отсутствии входного вы­ сокочастотного сигнала и отключенных компенсирующих обмотках 2' и 3'. Пр и подаче входного сигнала без ком­ пенсирующих обмоток выходной сигнал будет иметь вид,

ствия плоской части импульсного управляющего поля

83

Влияние управляющей цепи на выходную цепь можно уменьшить в основном за счет увеличения ее постоянной времени. Это возможно "в тех случаях, когда параметр быстродействия несуществен. В противном случае необ­ ходимо прибегать к компенсирующим обмоткам .

Результаты теоретического исследования модуляцион­ ного устройства с достаточной д л я инженерной практики точностью совпадают с экспериментами . Полученные количественные характеристики позволяют выработать требования как к используемым в модуляторе пленкам, так и к внешним цепям. Рассмотренное модуляционное устройство может применяться в качестве амплитудного модулятора, балансного модулятора, а т а к ж е ключевого устройства.

2.2.2. Параметром

Использование в качестве нелинейного управляемо - • го элемента тонкой ферромагнитной пленки позволяет

является разработка способов создания пленок с неизме­ няющимися со временем параметрами, с малыми потеря­ ми, обусловленными различными эффектами, и с задан ­ ными нелинейными характеристиками .

Теоретическое исследование параметронов на Т Ф П — достаточно трудоемкая задача . С целью иллюстрации применения эквивалентной схемы Т Ф П для количествен­ ного исследования тонкопленочного параметрона вос­ пользуемся методом гармонического баланса, применен­

стоит из сигнальной цепи (выходная цепь), цепи подкач­

лосковых линий — в зависимости от рабочей частоты. В отличие от схемы модуляционного устройства, сигналь­ ный контур параметрона настроен на частоту, вдвое меньшую частоты входного сигнала (подкачки) . П о л е подкачки и поле смещения действуют вдоль легкого на­ правления пленки, а сигнальное поле — вдоль трудного.

85

Основные соотношения, характеризующие работоспо­ собность параметрона м о ж е м получить, исследуя стацио­

86

Решение системы уравнений (2.24) и (2.26) в стацио­ нарном режиме будем искать в виде суммы гармоник ря­ да Фурье:

рактеризующие связь м е ж д у эквивалентной схемой плен­ ки и сигнального контура.

87

Подставляя (2.29) в (2.28), после несложных преобразо­ ваний получаем

В„„ = - а л + bndn

+ ~ & " с " sin (лш* - <?,,).

An

Р и с . 2.15

Согласно принципу гармонического баланса осуществим подстановку (2.31) в уравнение (2.26). После того как сгруппируем и приравняем нулю коэффициенты при си­ нусной и косинусной составляющих, будем иметь

Решая эти уравнения относительно квадратурных компо­ нент сигнального тока, получаем

88

ствующая частота всегда будет ниже определяемой этим

Сучетом этих преобразований уравнение, характеризую ­

ще е поведение пленки после перехода к безразмерному времени может быть представлено в виде

качки.

* Для рассматриваемого случая в выражении для дифферен­ циальной индуктивности будем учитывать только знак плюс.

89