Раздел 3 преобразования при изменении базиса

§ 1. Основные понятия и теоремы

Пусть в линейном пространстве Vзадан базис , и другой базис . Разложим векторыf_kв базисе :

Если координаты векторов f_k нового базиса в старом базисе записать в столбцы некоторой матрицы, то получим матрицу линейного оператораР, который переводит векторые_iв векторыf_i соответственно. Этот операторназывается оператором переходаот базиса {е_i} к базису {f_i}, а его матрицаназывается матрицей переходаи обозначаетсяР_{е  f}.

При переходе от базиса {е_i} к базису {f_i} различные объекты, заданные в линейном пространстве преобразуются по разному:

а) базисные векторы: ;

б) векторы ;

в) матрицы линейных операторов: ;

г) коэффициенты линейных форм: ;

д) матрицы билинейных форм: ,

и, кроме того, при последовательных преобразованиях: T_{е  g} =Р_{е  f} ^.G_{f  g}.

§2. Контрольные вопросы и задания

1. Как изменятся координаты вектора, если: а) один из базисных векторов умножить на 0; б) переставить местами два базисных вектора?

2. Как изменятся коэффициенты линейной формы, если: а) один из базисных векторов умножить на 0; б) переставить местами два базисных вектора?

3. Как изменится матрица линейного оператора, если: а) один из базисных векторов умножить на 0; б) переставить местами два базисных вектора?

4. Как изменится матрица билинейной формы, если: а) один из базисных векторов умножить на 0; б) переставить местами два базисных вектора?

5. Сохраняется ли свойство положительной определенности квадратичной формы при переходе от одного базиса к другому?

§3. Примеры решения задач

Задача 1. Пустьi,j– координатные векторы прямоугольной системы координат на плоскости. Найти разложение вектораx=i+jпо базису {e₁,e₂}, еслиe₁= 7i+ 4j,e₂= 5i+ 3j.

Решение. По определению, матрица перехода от базиса {i,j} к базису {e₁,e₂} есть матрица . Вычислим обратную матрицу: . Векторхв базисе {i,j} имеет вид:х = (1, 1). По формулеx_f=P^–1x_e, находим столбецх_е координат векторахв базисе {e₁,e₂}:

.

Следовательно, х= –2е₁+ 3е₂.

Задача 2. В пространствеV₂даны три базиса: {e₁,e₂}, {f₁,f₂} и {g₁,g₂} причемf₁=e₁–e₂,f₂=e₁+e₂;g₁= 3e₁+e₂,g₂= 5e₁+e₂. Найти матрицу перехода от базиса {f₁,f₂} к базису {g₁,g₂}.

Решение. По определению матрица перехода от базиса {e₁,e₂} к базису {f₁,f₂} есть матрица , а матрица перехода от базиса {e₁,e₂} к базису {g₁,g₂} есть матрица . Тогдаf_i = P_efe_i, g_i = P_ege_i.Из первого равенства находим . Подставляя во второе равенство, получаем .

Таким образом, матрицей перехода от базиса {f₁,f₂} к базису {g₁,g₂} является матрица . Вычисляем матрицу : , а затем находим произведение :

.

Задача 3.Пустьi,j– координатные векторы прямоугольной системы координат на плоскости. Найти матрицу перехода от базиса {i,j} к базису {i,j}, повернутому на уголпо отношению к базису {i, j} и матрицу обратного перехода.

Решение. Из рис.1 ясно, что координаты векторовi,jв базисе {i,j} имеют видi= {cos, sin},j= {–sin, cos}. Пользуясь определением, составляем матрицу переходаА() переходя от базиса {i,j} к базису {i,j}:

. (1)

В

ычисляем матрицуА^–1() обратного перехода:

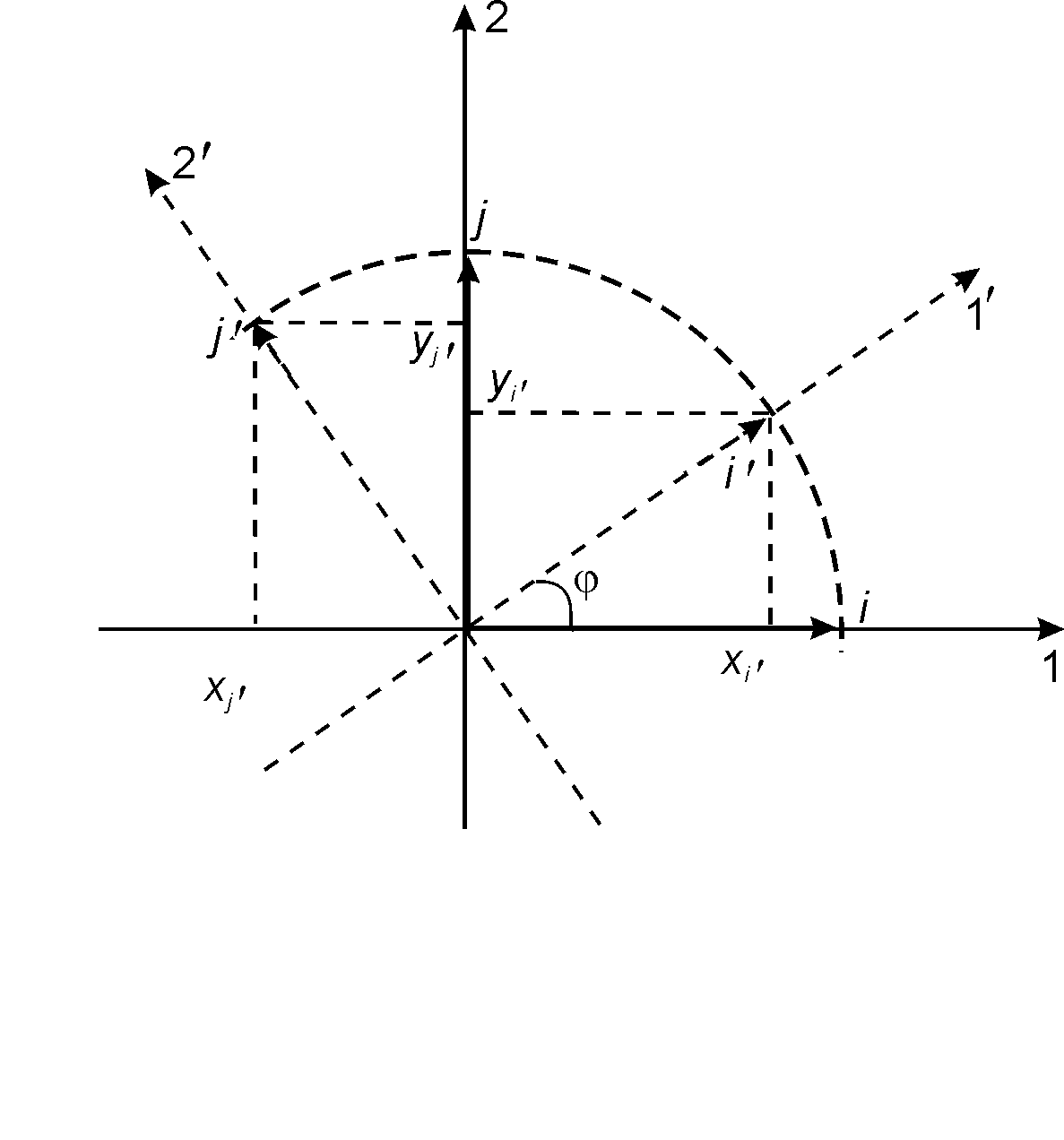
Рис.1. Поворот прямоугольной системы координат на угол против часовой стрелки.

. Отметим, что обратный переход от базиса {i,j} к базису {i,j} есть поворот базиса на угол (–), и поэтому матрицу этого перехода можно найти по формуле (1), заменивна (–):

А^–1() =А() =.

Задача 4. Билинейная форма(x,y) в базисе {e₁,e₂,e₃} имеет вид(x,y) = –2х₁у₁+ 3х₁у₂+х₁у₃+ 5х₂у₁+х₂у₃–х₃у₂. Найти выражение этой билинейной формы через координаты элементов в базисе {f₁,f₂,f₃}, еслиf₁ =e₂,f₂= –e₁,f₃ =e₂+e₃.

Решение. Составим матрицуРперехода от базиса {e₁,e₂,e₃} к базису {f₁,f₂,f₃} (со столбцами из координат элементовf₁,f₂,f₃ в базисе ):

,

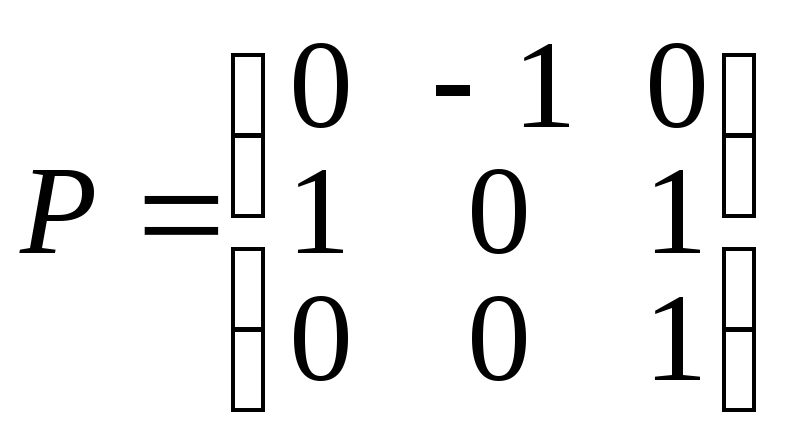и воспользуемся формулой B_f=P^TB_ePпреобразования матрицы билинейной формы при изменении базиса, гдеВ_e иВ_f– матрицы билинейной формы(x,y) в базисах {e₁,e₂,e₃} и {f₁,f₂,f₃}.

Составим матрицу В_e: . Далее вычисляем:

.

отсюда получаем следующий вид билинейной формы в базисе {f₁,f₂,f₃}:

(x,y) = –5₁₂+₁₂– 3₂₁– 2₂₂– 4₂₃–₃₁– 5₃₂,

где .

Задача 5. Привести уравнение кривой второго порядка

11x²– 20xy– 4y²– 20x– 8y+ 1 = 0 к каноническому виду с помощью поворота осей координат системыOxyи последующего параллельного переноса.

Решение. Приведем квадратичную форму 11x²– 20xy– 4y², связанную с заданным уравнением, ортогональным преобразованием к каноническому виду. С этой целью составим матрицу квадратичной формы: , и запишем характеристическое уравнение:

.

Оно имеет корни ₁= –9,₂= 16. Далее находим взаимно ортогональные нормированные собственные векторы (столбцы)F₁иF₂матрицыА: если₁= –9, то ; если₂= 16, то .

Следовательно, искомое ортогональное преобразование имеет матрицу , у которой detP= 1. Равенство единице определителя ортогонального преобразования обозначает, что происходит поворот системы координат без отражения относительно одной из осей, т.е. без изменения ориентации системы координат. МатрицаРявляется матрицей оператора поворота на уголтакой, что . Повернув оси координат системыОхуна угол (против часовой стрелки), получим прямоугольную системуОху. При этом координаты точек преобразуются по формуле или

.

При таком ортогональном преобразовании квадратичная форма переходит в форму: ₁(x )²+₂(y )²= –9(x )²+ 16(y )². Запишем в новых координатах линейные члены заданного уравнения:

.

В системе координат Охууравнение кривой принимает вид:

.

Выделяя полные квадраты по обеим переменным, получаем:

.

Полагая , т.е. производя параллельный перенос осей координат так, что начало координат, переходит в точку , приходим к каноническому уравнению данной кривой

.

Это – каноническое уравнение гиперболы в системе координат Оху.

Задача 6. С помощью поворота осей координат и последующего параллельного переноса привести уравнение кривой второго порядка 4x²– 4xy+y²– 2x– 3y+ = 0 к каноническому виду.

Решение. Составляем матрицу квадратичной формы, связанной с заданным уравнением: , и решаем характеристическое уравнение

.

Оно имеет корни ₁= 0,₂= 5. Находим взаимно ортогональные нормированные собственные векторы матрицыА:

, .

Они являются столбцами матрицы Рортогонального преобразования, приводящего квадратичную форму к каноническому виду:

.

Следовательно, преобразование (как и в предыдущем примере) это поворот на угол и координаты точек преобразуются по формулам: . Пользуясь этими формулами, запишем линейные члены заданного уравнения в координатахх,у:

.

Итак, уравнение данной кривой в системе координат Оху полученной из системыОхуповоротом осей на угол , имеет вид:

.

В результате выделения полного квадрата по переменной у получаем уравнение .

Положим х=х+ 1,у=у+ 0,7, т.е. произведем параллельный перенос осей координат системыОху так, что начало координат перейдет в точкуО (–1; –0,7). В системе координатОху уравнение кривой имеет канонический вид: (у )²= –0,8х. Это – каноническое уравнение параболы.

Задача 7. Перейти к такой прямоугольной системе координат, в которой уравнение поверхности 3y²+ 3z² + 4xy+ 4xz– 2yz – 12x– 14y+ + 2z+ 506 = 0 имеет канонический вид, и определить тип поверхности.

Решение. Квадратичная форма 3y²+ 3z² + 4xy+ 4xz– 2yz, связанная с заданным уравнением, имеет матрицу 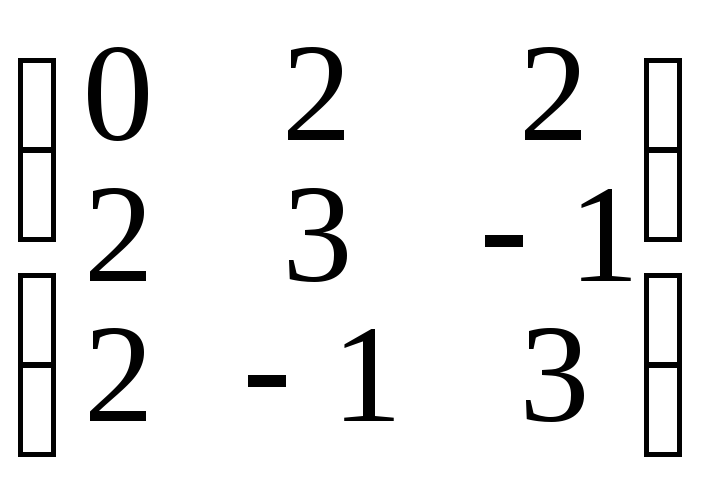. Собственные значения этой матрицы есть₁= –2,_2,3= 4, а столбцы (векторы)

, ,

являются попарно ортогональными нормированными ее собственными векторами. Определитель матрицы, составленной из этих столбцов, равен ­–1. Это означает, что ортогональное преобразование является поворотом с отражением относительно одной из координатных плоскостей. Во избежание этого поменяем местами, первый и второй столбцы в матрице (f₁ f₂ f₃), получим ортогональную матрицу: ,

определитель которой равен единице, т.е. преобразование не будет производить отражения.

Ортогональное преобразование переменных приводит квадратичную форму к следующему каноническому виду:

4(х )²– 2(y )²+ 4(z )².

С помощью формулы для ортогонального преобразования переменных вычислим в новых координатах линейные члены заданного уравнения:

.

Итак, в системе координат Охуzс координатными векторамиi,j,kуравнение поверхности имеет вид:

.

Выделив полные квадраты по переменным х иу, получим уравнение . Положим , , , т.е. произведем параллельный перенос осей координат системыОхуzтак, что начало координат перейдет в точку . В новой системе координатОхуzуравнение поверхности имеет канонический вид: . Это – уравнение однополостного гиперболоида.