Введение

Данные методические указания отражают многолетний опыт авторов по чтению лекций и ведению семинарских занятий по линейной алгебре на физико-техническом факультете Харьковского национального университета.

Трудно представить себе образование современного физика без знания и владения основными методами линейной алгебры. Линейной алгебре посвящена обширная литература, имеются прекрасно написанные учебники и задачники. Вместе с тем ощущается недостаток пособий, помогающих студентам выработать навыки решения задач по различным разделам линейной алгебры. Авторы данных указаний ставили перед собой цель в какой-то мере ликвидировать этот пробел.

Назначение указаний мы видим в том, чтобы активизировать самостоятельную работу студентов при изучении курса линейной алгебры, помочь активному и неформальному усвоению этого предмета.

Авторами задуман целый цикл методических указаний по различным разделам изучаемого курса «Высшая алгебра». Данные методические указания являются второй частью этого цикла и посвящены теме «Унитарные и евклидовы пространства».

Структура методических указаний подчинена решению, поставленных выше учебно-методических задач. Материал указаний разбит на четыре параграфа. В параграфе «Основные понятия и теоремы» приводятся без доказательства основные теоретические сведения (определения, теоремы, формулы), необходимые для решения задач. В параграфе «Контрольные вопросы и задания» содержатся вопросы по теории и простые задачи, решение которых не связано с большими вычислениями, но которые хорошо иллюстрируют то или иное теоретическое положение. Назначение параграфа – дать возможность студенту самому проконтролировать усвоение основных понятий. Предполагается, конечно, что основная работа над теоретическим материалом с проработкой доказательств теорем ведется по учебнику или конспекту лекций. В параграфе «Примеры решения задач» представлены решение типичных задач по изучаемой теме. Назначение параграфа «Задачи и упражнения для самостоятельной работы» отражено в его названии. Из этого раздела подбираются задачи для решения на практических занятиях, для домашних заданий по заданному разделу.

§ 1. Основные понятия и теоремы

В линейном пространстве Vнад числовым полемK определено скалярное произведение, еслии выполнены четыре аксиомы:

1° , еслиKC и, еслиK R;

2° ;

3° ;

4° , причем.

Комплексное конечномерное линейное пространство со скалярным произведением (KC) называется унитарным пространством.

Вещественное конечномерное линейное пространство со скалярным произведением (K R) называется евклидовым пространством. (Если в дальнейшем тексте написан знак «^–» комплексного сопряжения, то в евклидовом пространстве он не пишется).

Если в пространстве V со скалярным произведением задан базис {e_i}ⁿ, то, т.е. чтобы задать скалярное произведение достаточно задать матрицу с матричными элементами. Эта матрица называется матрицей Грамма.

Длиной (нормой) вектора хназывается величина. Другое обозначение нормы вектора –║х║ = .

В евклидовом пространстве углом  между векторамихиуназывается угол между 0 такой, что.

В унитарном пространстве содержательного понятия угла нет.

Векторы хиуевклидового или унитарного пространства называются ортогональными, если (х,у) = 0. Система векторовназывается ортогональной, если (f_i,f_j) = 0 дляi  j. Система векторовназывается ортонормированной, если.

В каждом евклидовом и унитарном пространстве существует ортонормированный базис. При этом, в ортонормированном базисе :

и.

Получить ортонормированный базис пространства Vиз произвольного базисаf₁,f₂, … ,f_nможно с помощью процесса ортогонализации:

Положим: e₁=f₁;e₂=f₂ + e₁. Здесьподбирается из условияe₁e₂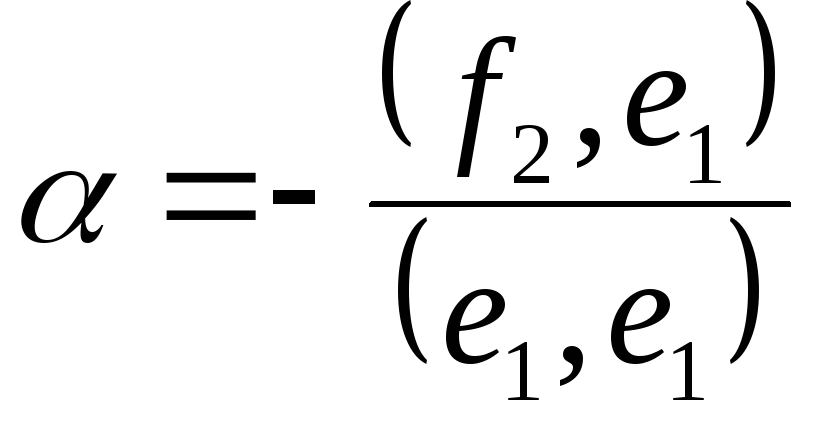.e₃=f₃ +₁ e₁+₂ e₂и₁,₂ищутся из условийe₁e₃,

е₂e₃: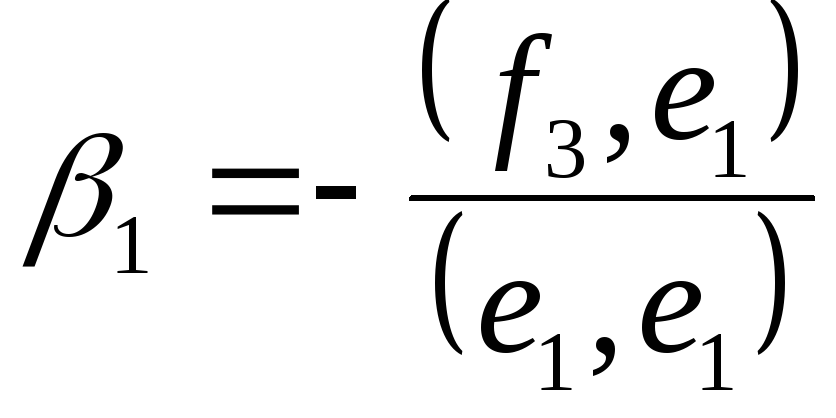;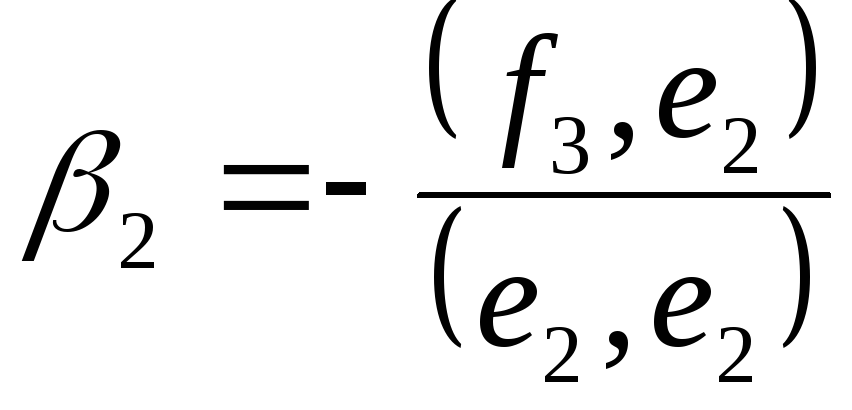и т.д.

e_k=f_k +₁ e₁+₂ e₂+ … +_k-1 e_k-1и

;; … ;.

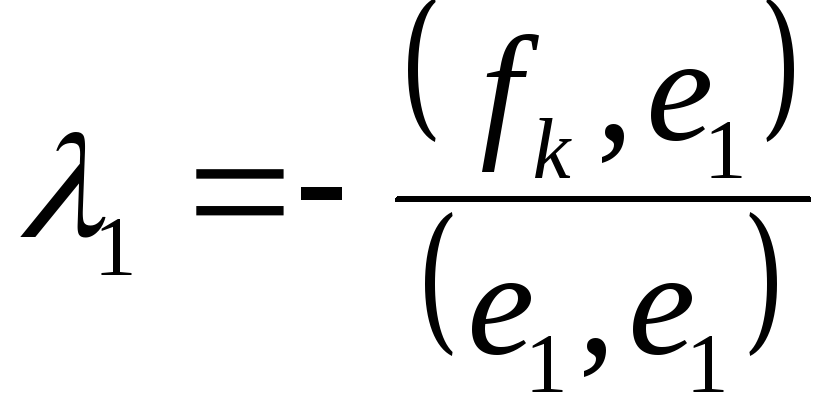Нормируя векторы e_k полученного базиса, мы сделаем его ортонормированным. Описанный процесс получения ортогонального базиса из заданного не ортогонального базиса, называетсяпроцессом ортогонализации Штурма.

Два евклидовых или унитарных пространства VиVназываются изоморфными, если они изоморфны как линейные пространства и, кроме того,x,yVx,yVтакие, чтоx  x, y y. Тогда (x,y) = (x,y).

Если два евклидовых или унитарных пространства изоморфны, то в них можно ввести одинаковую норму.

Вектор hназывается перпендикулярным к подпространствуL(hL) еслиyL(h,y) = 0.

Ортогональным дополнением L^к подпространствуLназывается:

L^{hV|hL}.

При этом, L^ само является подпространством и:

а) V=L L^, б) dimL+ dimL^ = dimV.

Пусть L– подпространствоV:

xVx₀L,x^L^ |x=x₀+x^.

x₀–называется ортогональной проекцией вектора x на подпространство L,

x^– называется ортогональной составляющей вектора x относительно L.

Длина вектора x^(|x^|) называется расстоянием между векторомx и подпространствомL.

Для евклидового пространства Vугол между векторамиx иx₀называется углом между векторомx и подпространствомL.

Если – ортогональный базис вV, то

.

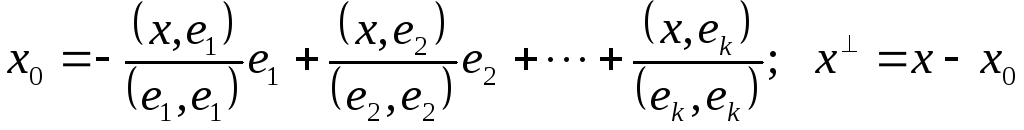Если М=у+Lмногообразие линейного подпространстваL, то расстоянием между подпространствомL и многообразиемМ называется длина ортогональной составляющейу^вектора сдвигау относительно подпространстваL.