
§ 4.Задачи и упражнения для самостоятельной работы
Будет ли пространство евклидовым, если в трехмерном геометрическом пространстве за скалярное произведение принять:
а) произведение длин двух векторов?
б) произведение длин двух векторов на косинус угла между ними?
в) удвоенное обычное скалярное произведение этих векторов?
а) нет; б)
да; в) да.
Можно ли в двухмерном вещественном линейном пространстве скалярное произведение (х.у) векторовх(х1,х2) иу(у1,у2) определить формулами:
а) (х,у) =х2у1; б) (х,у) =х1у1 + 2х1у2+ 10х2у2;
в) (х,у) =х1у2 +х2у1; г) (х,у) = 2х1у1 + 3х2у2;
д) (х,у) =х1у1 – 2х1у2– 2х2у1+ 5х2у2;
е) (х,у) = 7х1у1 + 6х1у2+ 6х2у1+ 9х2у2;
ж) (х,у) = 9х1у1 – 3х1у2– 3х2у1+х2у2;
з) (х,у) = 2х1у1 + 2х1у2+ 2х2у1+х2у2.
а) ,б) нет; нарушено
10;
в) нет; нарушено 40;
г), д), е) да; ж) нет; нарушено 40;
з) да.
3. Доказать, что в двухмерном вещественном
линейном пространстве функция F(x,y) =a11x1y1+a12x1y2+a21x2y1+a22x2y2, гдеx1,x2,y1,y2– координаты векторовx иyв некотором базисе, задает скалярное
произведение тогда и только тогда, когдаa21=a12,a11> 0,a11a22–![]() > 0.
> 0.
Можно ли в двухмерном комплексном пространстве скалярное произведение (x,y) векторовx(х1,x2) иy(y1,y2) определить формулами:
а) (х,у) =х1у1 +х2у2;
б) (х,у) =х1![]() ;
;
в) (х,у) = iх1![]() +iх2
+iх2![]() ;
г) (х,у) = iх1
;
г) (х,у) = iх1![]() –iх2
–iх2![]() ;
;
д) (х,у) = (3 +i)х1![]() +
(3 –i)х2
+
(3 –i)х2![]() ;
е) (х,у) =3х1
;
е) (х,у) =3х1![]() +
4х2
+
4х2![]() ;
;
ж) (х,у) =5х1![]() +iх2
+iх2![]() ;
з) (х,у) =х1
;
з) (х,у) =х1![]() +
(1+i)х1
+
(1+i)х1![]() +
(1–i)х2
+
(1–i)х2![]() +3х2
+3х2![]() .
.
а), б) нет; нарушено 10; в) нет; нарушено 10; г) нет; нарушено 40; д) нет; нарушено 40;
е) да; ж) нет;
нарушено 10;
з) да.
Обозначив через х1,х2 иу1,у2 координаты векторовхиу в некотором базисе двухмерного комплексного линейного пространства, найти условия на комплексные коэффициентыa11,a12,a21 иa22 необходимые и достаточные для того чтобы функцияF(x,y) = =a11x1
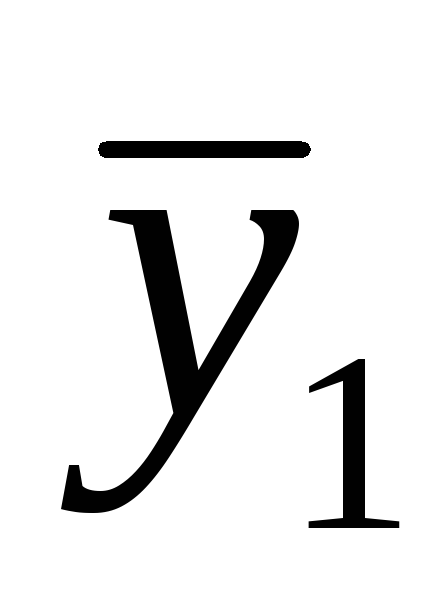 +a12x1
+a12x1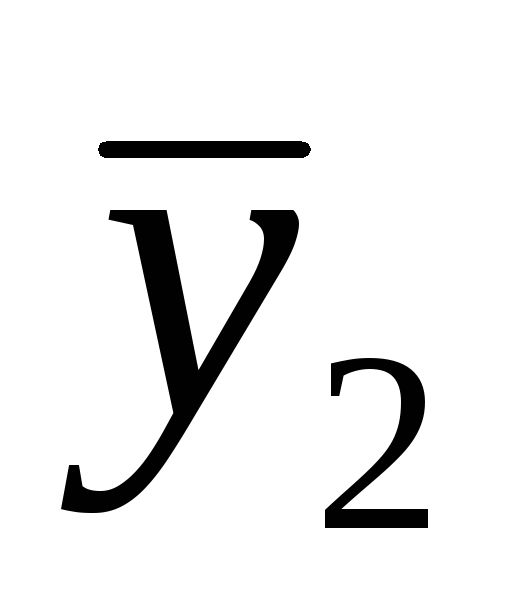 +a21x2
+a21x2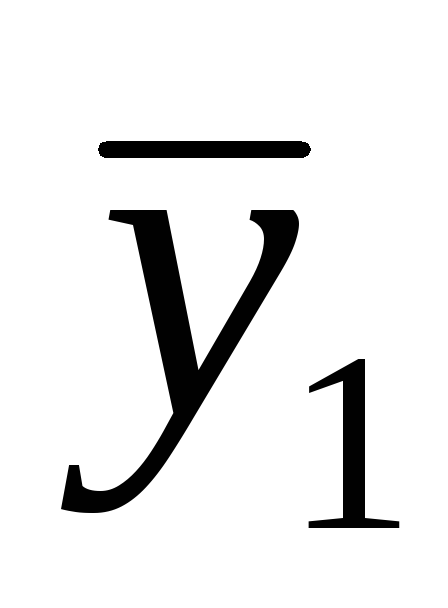 +a22x2
+a22x2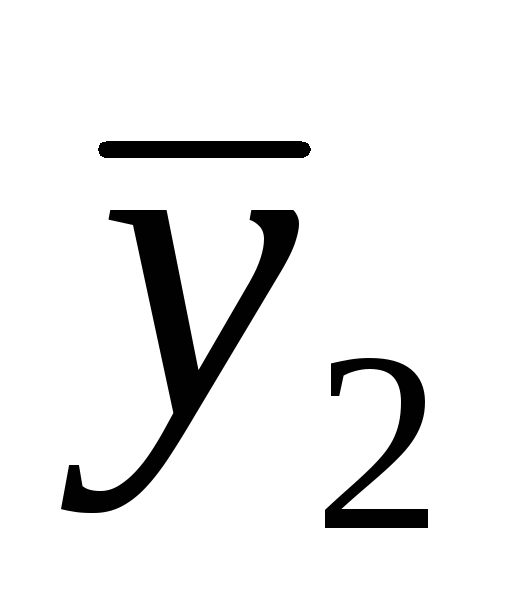 определяла унитарное скалярное
произведение.
определяла унитарное скалярное
произведение.
a21
= ![]() ;a11
> 0; a22
> 0; a11
a22
– | a12
|2
> 0.
;a11
> 0; a22
> 0; a11
a22
– | a12
|2
> 0.
В пространстве полиномов степени не выше трех можно ли скалярное произведение задать так:
![]() .
.
А для полиномов степени не выше двух?
n =
3, нет; нарушено 40;
n
= 2, да.
В пространстве полиномов с комплексными коэффициентами степени не выше n можно ли скалярное произведение полиномов
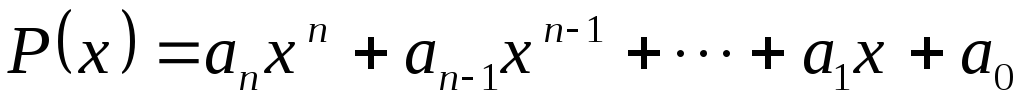 и
и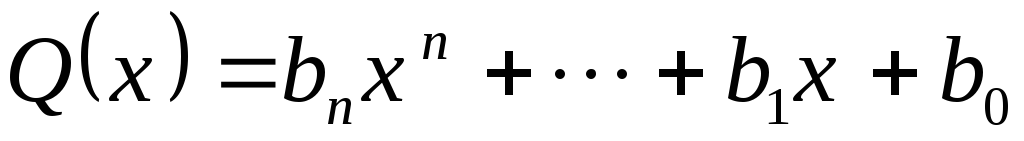 формулами:
формулами:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
а) да; б)
нет; нарушено 40;
в) да.
Показать, что в линейном пространстве полиномов степени не выше n с вещественными коэффициентами скалярное произведение
может быть задано формулами:
а)
![]() ,
где0,1,
… ,nи0,1,
… ,nкоэффициенты полиномовPиQ;
,
где0,1,
… ,nи0,1,
… ,nкоэффициенты полиномовPиQ;
б)
![]() ,
где
,
где![]() и
и![]() – производныеk-го порядка многочленовPиQ в некоторой точкех=а,аR.
– производныеk-го порядка многочленовPиQ в некоторой точкех=а,аR.
Можно ли принять за скалярное произведение в пространстве непрерывных функций, заданных на соответствующих интервалах следующие выражения:
а)
![]() на (–1, 1); б)
на (–1, 1); б)![]() на (0, 1);
на (0, 1);
в)
![]() на (–1, 1); г)
на (–1, 1); г)![]() на (–1, 1);
на (–1, 1);
д)
![]() на (0, 1); е)
на (0, 1); е)![]() на (0,);
на (0,);
ж)
![]() на (0, 1); з)
на (0, 1); з)![]() на (0, 1);
на (0, 1);
и)
![]() на (
на (![]() ).
).
а) нет; нарушено 40; б) да; в) да; г) нет; нарушено 40; д) нет; нарушено 20 и 30;
е) да; ж) да;
з) да, если V
вещественно и нет, если Vкомплексно; и)
да.
Найти длину вектора харифметического пространства с заданными скалярным произведением:
а) х(5, 4, 3), в стандартном скалярном произведении;
б) х(1, -2, 3, 4), в стандартном скалярном произведении;
в) х(1, 1), (х,у) =х1у1+х1у2 +х2у1 + 3х2у2 ;
г) х(1, –1, 2), (х,у) = 4х1у1+ 2х1у2 + 2х2у1 + 2х2у2 –х2у3 –х3у2 + 3х3у3;
д) х(1,i), (х,у) = 2х1![]() + (1+i)х1
+ (1+i)х1![]() +
(1–i)х1
+
(1–i)х1![]() +
3х1
+
3х1![]() ;
;
е) х(1+i, 1–i), (х,у)
=х1![]() –iх1
–iх1![]() +iх2
+iх2![]() +
2х1
+
2х1![]() +(2+i)х2
+(2+i)х2![]() +
+
+ (2–i)х3![]() +6х3
+6х3![]() .
.
Составить матрицы Грамма соответствующих скалярных произведений.
а) 5![]() ,
,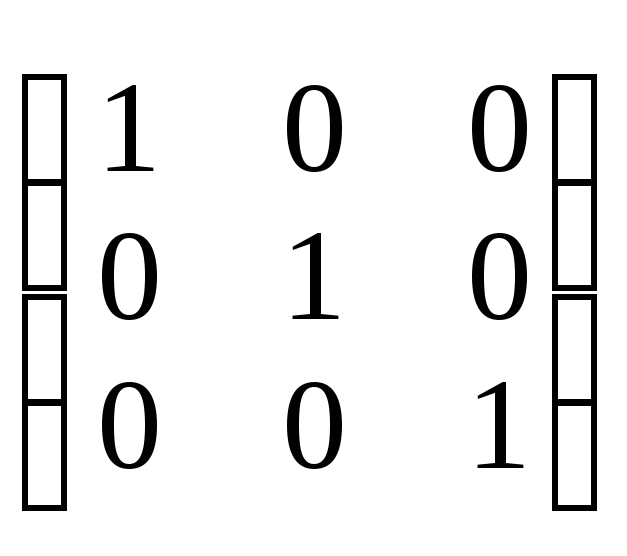 ;
б)
;
б)![]() ,
, ;
в)
;
в)![]() ,
,![]() ;
г) 3
;
г) 3![]() ,
,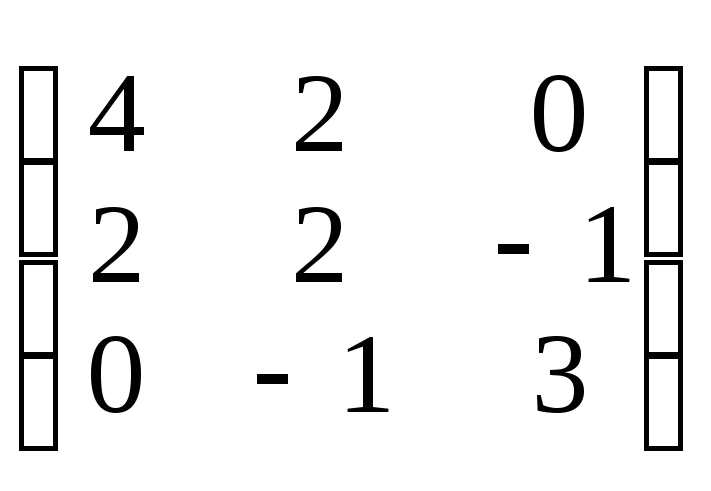 ;
;
д)
![]() ,
,![]() ;
е)
;
е)![]() ,
,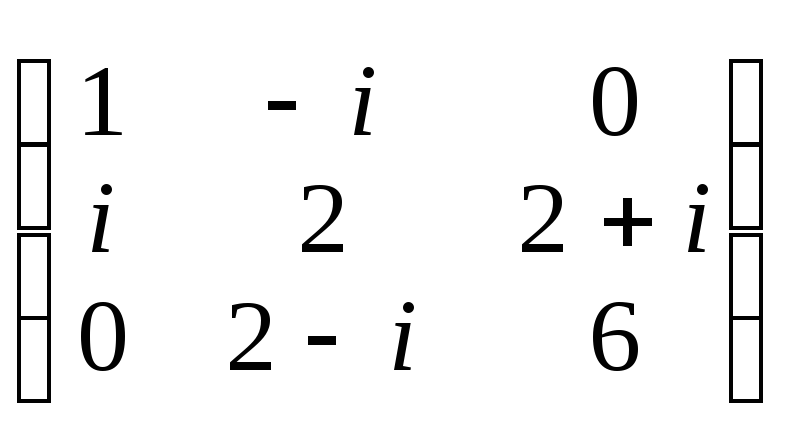 .
.
Найти угол между данными векторами в Е3со стандартным скалярным произведением:
а) (2, – 3, 1), (4, – 6, 2); б) (1, – 1, 2), (1, 0, 1); в) (1, 0, –1), (–1, 2, 2).
а) 0;
б)
/6; в)
3
/4.
Найти угол между данными векторами в Е4со стандартным скалярным произведением:
а) (1, –1, 1, –1), (–1, 1, –1, 1); б) (–1, 2, 3, –4), (5, 0, –2, 1);
в) (1, 2, 2, 1), (1, 1, 1, 2).
а) ;
б) 2
/3; в)
arccos
![]() .
.
Найти угол между векторами в Е2со скалярным произведением (х,у) =х1у1+х1у2 +х2у1 + 3х2у2:
а) (1, 0), (0, 1); б) (1, 0), (–1, 1).
а) arccos
![]() ;
б)
/ 2.
;
б)
/ 2.
Найти угол между векторами в Е3со скалярным произведением (х,у) = 4х1у1+ 2х1у2 + 2х2у1 + 2х2у2 –х2у3 –х3у2 + 3х3у3:
а) (1, 0, 0), (0, 1, 0); б) (–1, 0, 0), (–1, 2, 2).
а)
/ 4; б)
/ 2.
В пространстве Е4 в стандартном скалярном произведении опре-
делить (х,у) и угол между векторамихиу:
а) х(2, 1, 3, 1),у(1, 2, –2, 2); б)х(1, 2, 2, 3),у(3, 1, 5, 1);
в) х(1, 1, 1, 2),у(3, 1, –1, 0).
а) 0,
/ 2; б)
18,
/ 4; в) 3,
arccos
![]() .
.
В стандартном скалярном произведении найти нормированный вектор, ортогональный к векторам (1, 1,1,1), (1,–1, –1, 1), (2, 1, 1, 3).
один из
векторов
![]() .
.
Найти какой-нибудь нормированный вектор, ортогональный к данной системе векторов арифметического пространства с заданным скалярным произведением:
а) (2, 2, 1), (–2, 2, 3) в стандартном скалярном произведении;
б) (1, 2, 1, 0), (1, 1, 1, 1) в стандартном скалярном произведении;
в) (1, –1, 2), в стандартном скалярном произведении;
г) (1, 1), (х,у) =х1у1+х1у2 +х2у1 + 3х2у2 ;
д) (1, 2, 0), (2, 0, –1), (х,у) = 4х1у1+ 2х1у2+2х2у1+2х2у2–х2у3–х3у2+3х3у3;
е) (1+i, 1–i), в стандартном скалярном произведении;
ж) (–1, 1+i, 0), в стандартном скалярном произведении.
а) 1/3(1, -2, 2); б)
например, 1/2(1, -1, 1, -1); в) например,
![]() (1,
1, 0); г)
(1,
1, 0); г)![]() (2,
-1);
(2,
-1);
д)
![]() (1,
-1, 1); е) 1/2(1+i,
-1+i);
ж) 1/2(1–i,
1, –i).
(1,
-1, 1); е) 1/2(1+i,
-1+i);
ж) 1/2(1–i,
1, –i).
Применить процесс ортогонализации к линейно-независимой системе векторов вещественного арифметического пространства со стандартным скалярным произведением
(х,у) =х1у1+х1у2 + … +хnуn:
а) (1, –3, 1), (4, –5, 3); б) (1, 0, –1, 3), (2, 1, –1, 3);
в) (2, 0, 1), (4, –5, 3),(1, 7, –3); г) (1, 2, 2), (1, 1, 0), (0, 1, –4);
д) (2, 1, –2), (4, 1, 0), (0, 1, 0); е) (1, 1, –1, 0), (1, 2, 0, –1), (0, 0, 1, 0).
а) (1, -3, 1), (2, 1, 1); б) (1, 0, -1, 2), (1, 2, 1, 0); в) (2, 0, 1), (1, -1, -2), (1, 5, -2);
г) (1, 2, 2), (2, 1, -2), (2, -2, 1); д) (2, 1, -2), (1, 0, 1), (-1, 4, 1);
е) (1, 1, -1, 0),
(0, 1, 1, -1), (1, 0,1,1).
Система векторов задана в ортонормированном базисе евклидового или унитарного пространства своими координатами. Пользуясь процессом ортогонализации Штурма, построить ортонормированный базис в линейной оболочке этих векторов:
а) (1, 2, 1), (4, 4, 1), (–1, –3, –1); б) (1, 1, –1), (–4, 0, 5), (–8, 2, 0);
в) (3, –1, –2), (4, 0, –1), (5, 1, 0); г) (1, 2,–1, 1), (–5, –5, 4,–2), (–3, 6, 2,0);
д) (1, 0, 1, –1), (6, 0, 4, –5), (3, 2, –5, 4);
е) (1, –3, 2, 1), (–1, 7, –3, –2), (2, –2, 3, 1);
ж) (1, –1, 1, –1), (4, –2, 4, –2), (–2, 7, –4, 7), (2, 7, 2, 5);
з) (i, 1, –i), (2, 0, –1), (0, 2, –i);
и) (1, –1, 1 + i), (1, –i, –2 +i), (1 + 2i, 4 –i, –1).
а)
![]() (1,
2, 1),
(1,
2, 1),![]() (1,
0, -1),
(1,
0, -1),![]() (1,
-1, 1); б)
(1,
-1, 1); б)![]() (1,
1, -1),
(1,
1, -1),![]() (-1,
3, 2),
(-1,
3, 2),
![]() (-5,
1, -4); в)
(-5,
1, -4); в)
![]() (3,
-1, -2),
(3,
-1, -2),![]() (1,
1, 1); г)
(1,
1, 1); г)![]() (1,
2,-1, 1),
(1,
2,-1, 1),![]() (-2,
1, 1, 1),
(-2,
1, 1, 1),
![]() (0,
2, 1,-3); д)
(0,
2, 1,-3); д)![]() (1,
0, 1,-1),
(1,
0, 1,-1),![]() (1,
0, -1, 0),
(1,
0, -1, 0),![]() (1,
2, 1, 2); е)
(1,
2, 1, 2); е)![]() (1,
-3, 2, 1),
(1,
-3, 2, 1),
![]() (1,
1, 1, 0); ж) 1/2(1, -1, 1, -1), 1/2(1, 1, 1, 1),
(1,
1, 1, 0); ж) 1/2(1, -1, 1, -1), 1/2(1, 1, 1, 1),
![]() (1,
0, -1, 0),
(1,
0, -1, 0),![]() (0,
1, 0, -1);
(0,
1, 0, -1);
з)
![]() (i,
1, -i),
(i,
1, -i),
![]() (1,i,
0); и) 1/2(1, -1, 1+i),
(1,i,
0); и) 1/2(1, -1, 1+i),
![]() (1-i,
0, -1),
(1-i,
0, -1),
![]() (1,
3, 1+i).
(1,
3, 1+i).
Исходя из системы векторов f1,f2,f3арифметического пространства с заданным скалярным произведением с помощью процесса ортогонализации и нормировки построить ортонормированный базисе1,е2,е3, если:
а) f1(1, 0, 0),f2(0, 1, 0),f3(0, 0, 1);
) (х,у) = 4х1у1+ 2х1у2 + 2х2у1 + 2х2у2–х2у3 –х3у2 + 3х3у3;
) (х,у) =х1у1+ 2х1у2 + 2х2у1 + 5х2у2– 2х2у3 – 2х3у2 + 7х3у3;
б) f1(1, 0, –2),f2(0, 1, –2),f3(4, 0, 0);
(х,у) = 4х1у1+ 2х1у2 + 2х2у1 + 2х2у2–х2у3 –х3у2 + 3х3у3;
в) f1(0, 1, –1),f2(2, 0, 1),f3(–2, 4, 0);
(х,у) = 5х1у1–х1у2 –х2у1 +х2у2+ 2х1у3 + 2х3у1 + 4х3у3.
а. )
(1/2, 0, 0), (-1/2, 1, 0),
![]() (-1,
2, 2); а .)
(1, 0, 0), (-2, 1, 0),
(-1,
2, 2); а .)
(1, 0, 0), (-2, 1, 0),
![]() (-4,
2, 1),
(-4,
2, 1),
б) 1/4(1, 0,
-2),
![]() (-1,
1, 0), 1/4(-1, 4, 2), в)
(-1,
1, 0), 1/4(-1, 4, 2), в)![]() (0,
1,-1),
(0,
1,-1),![]() (-2,
-2, 1),
(-2,
-2, 1),
![]() (0,
4, 1).
(0,
4, 1).
Пусть е1,е2,е3– ортонормированная система базисных векторов трехмерного унитарного пространства. Показать, что система векторов:а1= 1/3(2е1+2е2–е3);а2= 1/3(2е1–е2+2е3);а1= 1/3(е1–2е2– 2е3) также образует ортонормированную систему базисных векторов этого пространства.
Ортонормировать базис: i– j,i+ 2j,i+ j–k.
![]() (i
– j),
(i
– j),
![]() (i
+ j),
- k.
(i
+ j),
- k.
Применяя процесс ортогонализации, построить ортогональный базис подпространства, натянутого на данную систему векторов:
а) (1, 2, 1, 3), (4, 1, 1, 1), (3, 1, 1, 0);
б) (1, 2, 2, –1), (1, 1, –5, 3), (3, 2, 8, –7);
в) (2, 1, 3, –1), (7, 4, 3, –3), (1, 1, –6, 0), (5. 7, 7, 8).
а) (1, 2, 1, 3), (10, -1, 1, -3), (19, -87, -61, 72); б) (1, 2, 2, -1), (2, 3, -3, 2), (2, -1, -1, -2);
в) (2, 1, 3, -1),
(3, 2, -3, -1), (1, 5, 1,10).
В ортонормированном базисе V4дополнить пару векторов до ортогонального базиса:
а) (1, 1, 1, 2), (1, 0, 1, –1); б) (1, –1, 2, 0), (–1, 1, 1, 3);
в) (1, 2, 1, 2), (1, 1, –1, –1); г) (4, 0,–1, 0), (1, –6, 1, 2).
а) (-1, 0, 1, 0), (1, -6, 1, 2); б) (1, 1, 0, 0), (1, -1, -1, 1); в) (1, -1, -1, 1), (2, -1, 2, -1);
г) (1, 1, 1, 2), (1,
0, 1, –1).
25. Построить ортонормированный базис пространства, приняв за два вектора этого базиса векторы е1(1/2, 1/2, 1/2,1/2),е2 (1/6, 1/6, 1/2,–5/6).
е1,
е2,е3=
![]() (0,
-4, 3, 1),е4=
(0,
-4, 3, 1),е4=
![]() (-13,
5, 6, 2).
(-13,
5, 6, 2).
Проверить, что векторы следующих систем попарно ортогональны
и дополнить их до ортогональных базисов:
а) (1, –2, 2, –3), (2, –3, 2, 4); б) (1, 1, 1, 2), (1, 2, 3, –3).
а) (2, 2, 1,
0), (5, -2, -6, -1); б) (1, -2, 1, 0), (25, 4, -17,
-6).
Найти векторы, дополняющие следующие системы векторов до ортонормированных базисов:
а) (2/3, 1/3, 2/3), (1/3, 2/3, –2/3); б) (1/2, 1/2, 1/2, 1/2), (1/2, 1/2,–1/2, –1/2).
а) (2/3, -2/3,
-1/3); б) (1/2, -1/2, 1/2, -1/2), (1/2, -1/2, -1/2,
1/2).
В пространстве всех многочленов степени не выше 2 на интервале (0, 1) скалярное произведение определено так:
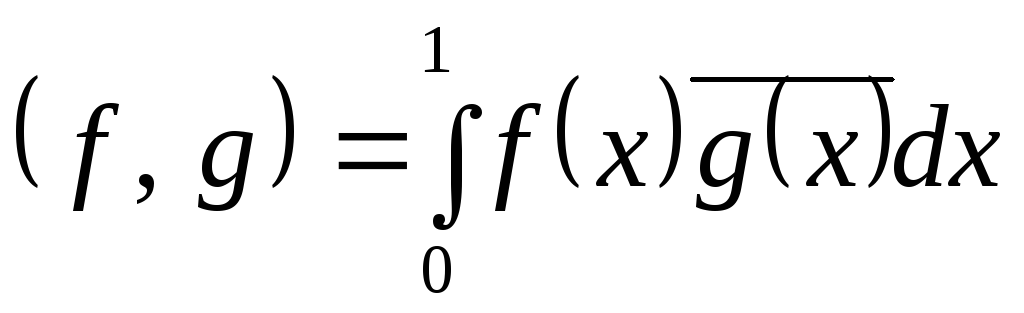 .
Показать, что это будет унитарное
пространство размерности 3. Показать,
что если в этом пространстве ортонормировать
последовательность 1,х,х2,
то получим 1,
.
Показать, что это будет унитарное
пространство размерности 3. Показать,
что если в этом пространстве ортонормировать
последовательность 1,х,х2,
то получим 1,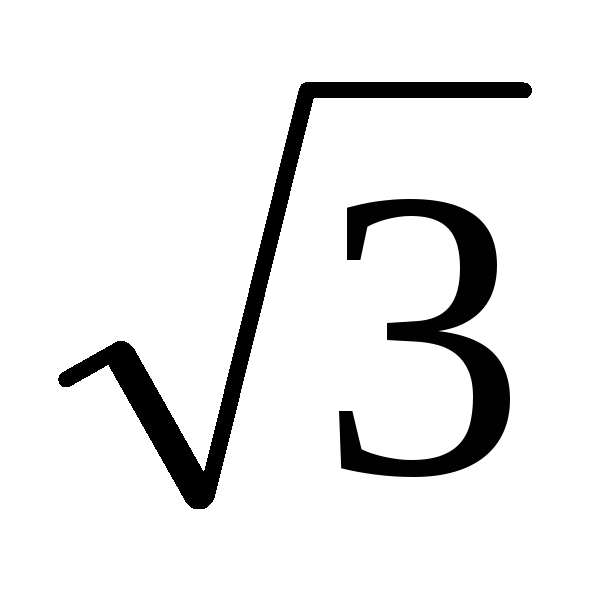 (2х– 1),
(2х– 1), (6х2– 6х+ 1).
(6х2– 6х+ 1).
Доказать, что полиномы вида
 образуют ортонормированную систему в
пространстве со скалярным произведением
образуют ортонормированную систему в
пространстве со скалярным произведением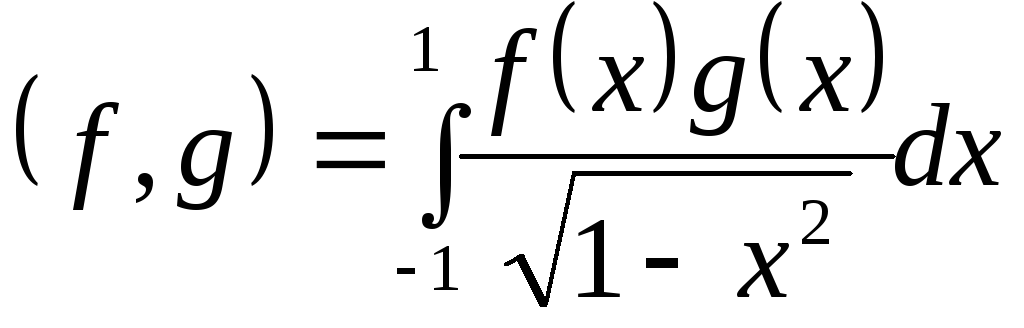 .
Эти полиномы называются полиномами
Чебышева I-го рода.
.
Эти полиномы называются полиномами
Чебышева I-го рода.
Многочлены, определенные формулами:
![]() ,k= 1, 2, 3, …
,k= 1, 2, 3, …
называются многочленами Лежандра.
Доказать, что многочлены ЛежандраL0,L1, … ,Lnобразуют ортогональный базис в евклидовом
пространствеРnмногочленов
степени не вышеnсо скалярным
произведением![]() .
Найти норму этих многочленов.
.
Найти норму этих многочленов.
![]()
В пространстве полиномов от х степени не выше 3 функции 1,х,х2,х3 образуют базис. Ортогонализовать этот базис, если скалярное произведение, задано формулой:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
В результате ортогонализации системы векторов 1, х,х2,х3 с помощью указанных скалярных произведений, получим первые четыре а) полинома Лежандра; б) полинома Чебышева I-го рода; в) полинома Эрмита.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Пусть V– пространство непрерывных функций на интервале (0, +
 ),
в котором определено скалярное
произведение
),
в котором определено скалярное
произведение
![]() .
.
Дан базис этого пространства {е-x,xе-x,x2е-x, …}. Проверить, будет
ли этот базис ортогональным и, если он не ортогонален, то найти
первые четыре элемента ортогонального базиса.
Не ортогонален;
![]() ,
,![]() ,
,![]() ,
,
![]() .
.
Найти базис ортогонального дополнения LподпространстваL, натянутого на векторы:а1(1, 0, 2, 1),а2(0, 1, –2, 1).
Например,
b1(2,
-2, -1, 0), b2(1,
1, 0, -1).
В трехмерном пространстве векторов построить ортогональное дополнение к подпространству векторов: (i–j). (i + j) + k.
Найти базис ортогонального дополнения LподпространстваL, еслиL задано системой уравнений:
 .
.
Например,
(1, 0, 6, 0), (3, 2, 0, -2).
В пространстве полиномов степени не выше 3 построить ортогональное дополнение к подпространству полиномов, обращающихся в нуль при х= 0. За скалярное произведение принять:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)![]() .
.
В ортогональном базисе
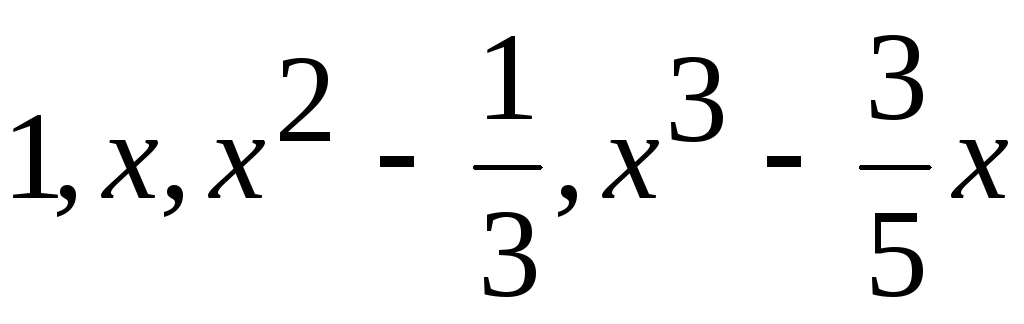 евклидового пространства со
скалярным произведением
евклидового пространства со
скалярным произведением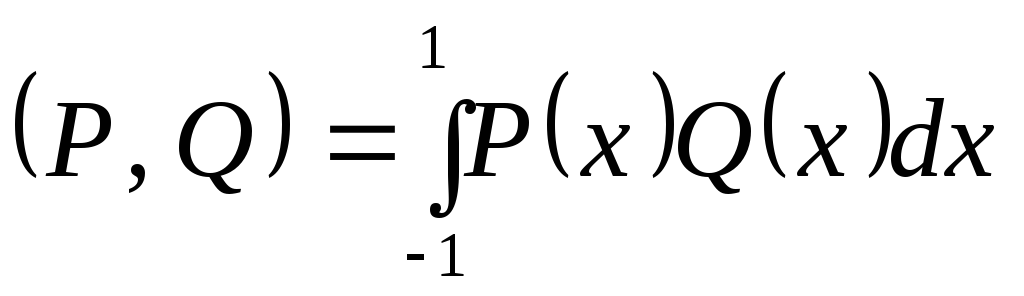 найти координаты вектора:
найти координаты вектора:
а) х3; б)х2; в)а3х3+а2х2+а1х+а0.
а) (0, 3/5, 0,
1); б) (1/3, 0, 1, 0); в) (а0
+а2/3,
а1
+(3/5)а3,
а2,
а3
).
Найти ортогональную проекцию вектора х3–х+ 1 на(1,х), если скалярное произведение задано в виде:
а)
![]() ;
б)
;
б)![]() .
.
а)
1 – (2/5)х;
б) х
– (2/7)х.
Найти проекцию вектора х3–iх+ 1 наℒ(1,х) со скалярным произведением
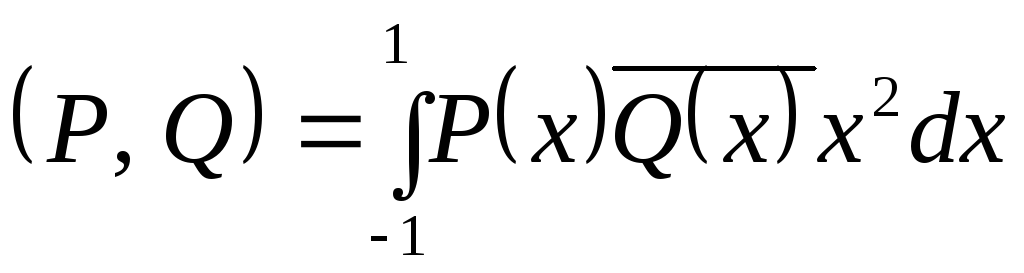 .1
+ (5/7 +i)х.
.1
+ (5/7 +i)х.
Подпространство Lевклидового пространства является линейной оболочкой векторов, заданных в некотором ортонормированном базисе пространства своими координатами. Найти ортогональную проекцию наL и ортогональную составляющую относительноL векторах, заданного в этом же базисе своими координатами:
а) а(10, –20, 10),х(0, 1, 0); б)а1(1, 1, 1),а2(4, 0, 5),х(7, –3, –1);
в) а(4, 3, 2, 1),х(1, –1, 1, –1); г)а1(1, –1, 1, 0),а2(2,–1, 0, 1),х(1, 0, 2,–2);
д) а1(1, –1, 1, 1),а2(1, 4, –1, 0),х(2, 1, 1, 0);
е) а1(1, 0, –1, 1),а2(3, 3, –2, 1),а3(–1, 6, 3, –5),х(1, 4, 0, 2);
ж) а1(2, 0, –1, –1),а2(1, –1, 1, –1),а3(1, 1, –1, –1),х(1, 2, 0, –1);
з) а1(1, 1, 1, 1),а2(5, 1, 1, 3),а3(3, –1, 1, 0),х(5, 4, –3, –2).
а) 1/3(-1, 2, -1), 1/3(1, 1, 1); б) (2, -2, 3), (5, -1, -4); в) 1/15(4, 3, 2, 1), 1/15(11, -18, 13,-16);
г) (0, -1, 2, -1), (1, 1, 0, -1); д) 1/2(3, 2, 1, 2), 1/2(1, 0, 1, -2); е) (2, 3, -1, 0), (-1, 1, 1, 2);
ж)
1/2(1, 3, -1, -3), 1/2(1, 1, 1, 1); з) (3, 0, -1, 2), (2, 4,
-2, -4).
Найти ортогональную проекцию уи ортогональную составляющуюzвекторахнаℒ(а1,а2, … ,аk):
а) х(4, –1, –3, 4),а1(1, 1, 1, 1),а2(1, 2, 2, –1),а3(1, 0, 0, 3);
б) х(5, 2, –2, 2),а1(2, 1, 1, –1),а2(1, 1, 3, 0),а3(1, 2, 8, 1);
в)
х(7, –4, –1, 2), аL задано уравнениями: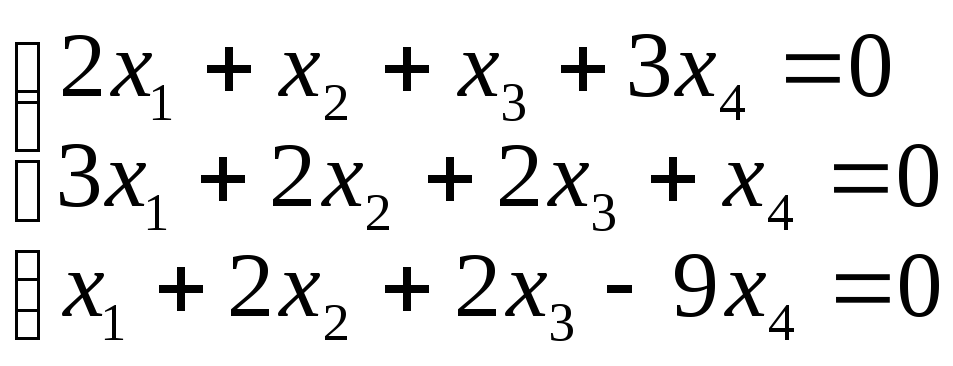 .
.
а) у = 3а1–2а2 = (1,-1,-1,5); z = (3,0,-2,-1); б) у = 2а1–а2 = (3,1,-1,-2); z = (2, 1,-1, 4);
в) у
= (5, -5, -2, -1); z
= (2, 1, 1, 3).
Найти ортогональную проекцию уи ортогональную составляю-
щую zвекторахна подпространствоLнатянутое на векторыа1,а2, … ,аk:
а) х(5, 2, –2, 2),а1(2, 1, 1, –1),а2(1, 1, 3, 0);
б) х(–3, 5, 9, 3),а1(1, 1, 1, 1),а2(2, –1, 1, 1),а3(2, –7, –1, 1).
а) у
(3, 1, -1, -2), z
(2, 1, -1, 4); б) у(1,
7, 3, 3), z(-4,
-2, 6, 0).
Линейное подпространство Lарифметического пространства со стандартным скалярным произведением натянуто на векторыf1,f2, … ,fm. Найти угол между векторомхи подпространствомL:
а) х(0, 1, 1),f1(1, 0, 1),f2(0, 1, 0); б)х(5, 1, –2),f1(1, –1, 2),f2(1, 1, 3);
в) х(1, –1, 0),f1(0, 2, 1),f2(1, 3, 0); г)х(–1, 1, 2),f1(1, 2, 1),f2(2, 1, –1);
д) х(–2, 2, 1, 0),f1(1, 2, 3, 0),f2(1, 0, 1, –2);
е) х(1, 0, 2, 1),f1(3, 3, –1, –1),f2(2, 1, 0, –2);
ж) х(1, 1, 0, 1),f1(1, –1, 1, –1),f2(1, 1, 3, 3),f3(3, –2, 4, –1);
з) х(1, 1, 1, 3),f1(1, –1, 1, –2),f2(1, 0, 1, –1),f3(3, 1, 2, –1);
а) /6;
б) /2;
в) arccos![]() ;
г) 0; д) arccos
;
г) 0; д) arccos![]() ;
е)/2;
ж) /4;
з) /6.
;
е)/2;
ж) /4;
з) /6.
Найти угол между ℒ(а1,а2, … ,аk) и векторомх:
а) х(1, 3, –1, 3),а1(1, –1, 1, 1),а2(5, 1, –3, 3);
б) х(2, 2, –1, 1),а1(1, –1, 1, 1),а2(–1, 2, 3, 1),а3(1, 0, 5, 3);
в) х(2, 2, 1, 1),а1(3, 4, –4, –1),а2(0, 1, –1, 2).
а)
/4;
б) /2;
в) /3.
Определить расстояние от точки х до линейного многообразияа0 +1а1 +2а2 +… +m аm:
а) х(1, 2, –1, 1),а0(0, –1, 1, 1),а1(0, –3, –1, 5),а2(4, –1, –3, 3);
б) х(0, 0, 0, 0),а0(1, 1, 1, 1),а1(1, 2, 3, 4).
а)
![]() ;
б)
;
б)![]() .
.
Найти расстояние от точки, заданной вектором хдо линейного многообразия, заданного системой уравнений:
а) х(4, 2, –5, 1); б)х(4, –1, 3, 7);
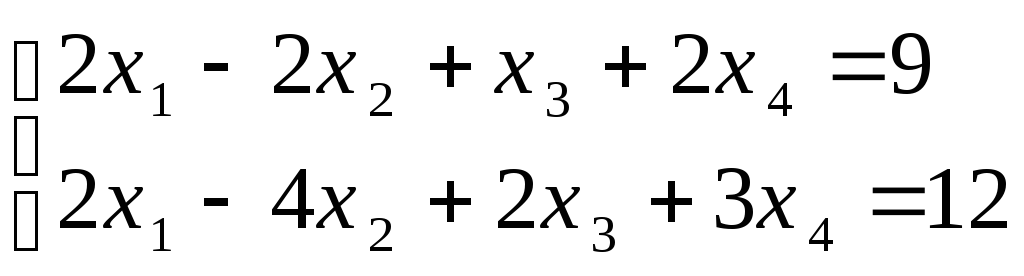 ;
;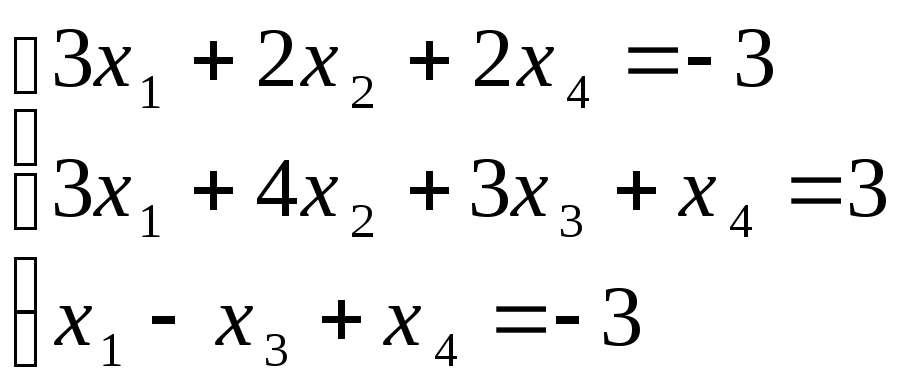 .
.
а)
5; б) 7.
Рассматривается пространство полиномов, степени не выше n. Скалярное произведение:
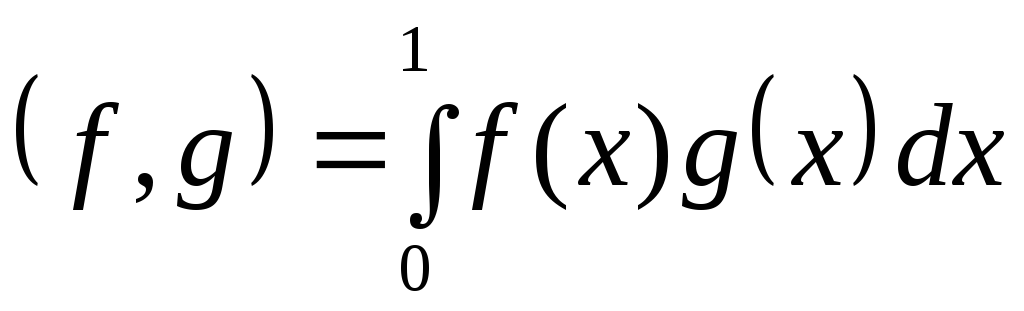 .
Определить расстояние от начала
координат до линейного многообразия
состоящего из полиномов:хn +а1хn-1+а2
хn-2+… +аn-1х+ аn .
.
Определить расстояние от начала
координат до линейного многообразия
состоящего из полиномов:хn +а1хn-1+а2
хn-2+… +аn-1х+ аn .
![]() .
.
Доказать, что определитель Грамма не изменится при применении к векторам а1,а2, … ,аkпроцесса ортогонализации, т.е. в результате ортогонализации векторыа1,а2, … ,аk перейдут в векторыb1,b2, …,bkиG(а1,а2, … ,аk) =G(b1,b2, … ,bk) = (b1,b1)(b2,b2)…(bkbk). Пользуясь этим выяснить геометрический смыслG(а1,а2) иG(b1,b2), предполагая векторы линейно-независимыми.
G(а1, а2) = квадрату площади параллелограмма на векторах а1, а2;
G(а1,
а2,
а3)
= квадрату объема параллелепипеда на
векторах а1,
а2,
а3.
Пусть есть система линейно-независимых векторов g1, g2, … ,gn. Доказать, что векторые1,е2, … ,еnполученные изg1, g2, … ,gn процессом ортогонализации имеют вид:
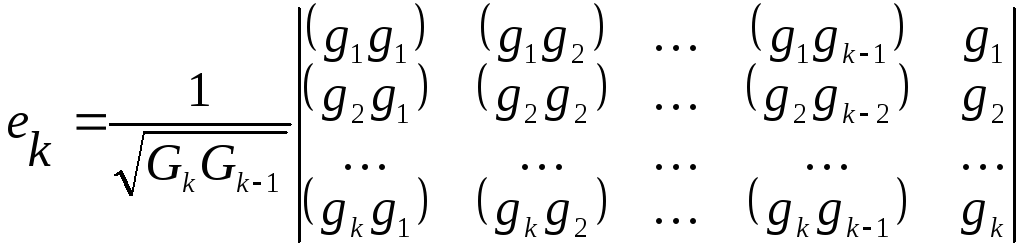 ,
,
где G0
= 1,Gk =G(g1,
g2, … ,gk) и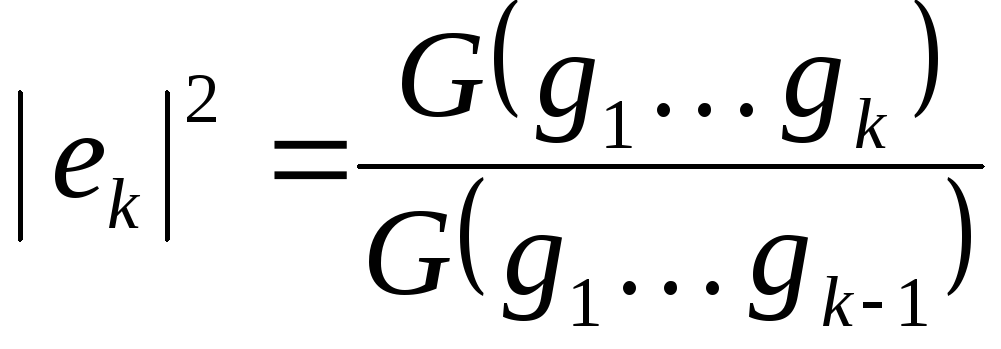 .
.
С помощью процесса ортогонализации Грамма (см. зад. 48), ортогонализовать следующие системы векторов:
а) (1, 2, 1), (4, 4, 1), (–1, –3, –1);
б) (1, 1, –1), (–4, 0, 5), (–8, 2, 0);
в) (3, –1, –2), (4, 0, –1), (5, 1, 0).
а)
![]() (1,
2, 1),
(1,
2, 1),![]() (1,
0, -1),
(1,
0, -1),![]() (1,
-1, 1); б)
(1,
-1, 1); б)![]() (1,
1, -1),
(1,
1, -1),![]() (-1,
3, 2),
(-1,
3, 2),
![]() (-5,
1, -4); в)
(-5,
1, -4); в)
![]() (3,
-1, -2),
(3,
-1, -2),![]() (1,
1, 1).
(1,
1, 1).
