Введение

Методические указания отражают многолетний опыт авторов по чтению лекций и ведению семинарских занятий по линейной алгебре на физико-техническом факультете Харьковского национального университета.

Трудно представить себе образование современного физика без знания и владения основными методами линейной алгебры. Линейной алгебре посвящена обширная литература, имеются прекрасно написанные учебники и задачники. Вместе с тем ощущается недостаток пособий, помогающих студентам выработать навыки решения задач по различным разделам линейной алгебры. Авторы данных указаний ставили перед собой цель в какой-то мере ликвидировать этот пробел.

Назначение указаний мы видим в том, чтобы активизировать самостоятельную работу студентов при изучении курса линейной алгебры, помочь активному и неформальному усвоению этого предмета.

Авторами разработан и издан цикл методических указаний по различным разделам курса «Высшая алгебра». Данные методические указания являются заключительной, шестой частью этого цикла и посвящены теме «Элементы теории групп и теории тензоров».

Структура методических указаний подчинена решению поставленных выше учебно-методических задач. Материал каждого раздела указаний разбит на четыре параграфа. В параграфе «Основные понятия и теоремы» приводятся без доказательства основные теоретические сведения (определения, теоремы, формулы), необходимые для решения задач. В параграфе «Контрольные вопросы и задания» содержатся вопросы по теории и простые задачи, решение которых не связано с большими вычислениями, но которые хорошо иллюстрируют то или иное теоретическое положение. Назначение параграфа – дать возможность студенту самому проконтролировать усвоение основных понятий. Предполагается, конечно, что основная работа над теоретическим материалом с проработкой доказательств теорем ведется по учебнику или конспекту лекций. В параграфе «Примеры решения задач» представлено решение типичных задач по изучаемой теме. Назначение параграфа «Задачи и упражнения для самостоятельной работы» отражено в его названии. Из этого параграфа подбираются задачи для решения на практических занятиях и для домашних заданий по заданному разделу.

Раздел I элементы теории групп

§ 1. Основные теоремы и определения

Def. Множество G элементов х, у, z ... произвольной природы назы­вается группой, если в нем корректным образом введена внутренняя операция (закон

композиции), т. е. х,yG zG такое, что z = ху (или z = х⊙у), удовле­творяющая следующим трем аксиомам:

1) xy(yz) = (xy)z; 1) x⊙y(y⊙z) = (x⊙y)⊙z;

2) G  хG х = х; 2) lG  хG х⊙e = х;

3) хG yG  xy = ; (y = –x) . 3) хG yG  х⊙y = e; (y = x^–1) .

В столбике слева приводится аддитивная форма записи аксиом групповой операции, а в столбике справа – мультипликативная форма записи тех же аксиом.

Если групповая операция есть операция сложения (есть, а не называется), то группа называется аддитивной. Если групповая операция есть операция умножения, то группа называется мультипликативной.

Первая аксиома выражает свойство ассоциативности операции и позволяет операцию, определенную для двух элементов множества, определить для любого конечного числа таких элементов. Вторая аксиома постулирует существование в множестве элемента нейтрального по данной операции. И, наконец, третья аксиома требует, чтобы для любого элемента множества существовал элемент этого же множества, который, взаимодействуя с заданным, дает нейтральный. В аддитивной группе такой элемент называется противоположным, в мультипликативной группе и в произвольной группе – обратным.

Если введенная операция еще и коммутативна, т. е.

4. xy = yx 4) x⊙y = y⊙х

то группа называется абелевой.

Def. Подмножество G₁ элементов G называется подгруппой, если:

1) х,yG₁ xyG₁; 2) G₁ ; 3) хG₁ (–x)G₁.

Если группа содержит конечное число элементов, то группа называ­ется конечной, а количество ее элементов называется порядком группы. Группа из элементов а⁰ = e, а, а², ... a^k = e называется циклической группой, порождаемой элементом а. Порядок группы – k.

Примеры групп. 1°. Группа симметрий ромба.

Рассмотрим множество преобразований ромба, в которое входят:

Е – тождественное преобразование;

S_BD – симметричное отражение относительно оси BD;

S_AC – симметричное отражение относительно оси АС;

S_O – симметричное отражение относительно точки О.

Закон композиции в множестве определим таблицей Кэли:

	Е	SBD	SAC	SO
Е	Е	SBD	SAC	SO
SBD	SBD	E	So	SAC
SAC	SAC	So	E	SBD
SO	SO	SAC	SBD	E

Множество рассмотренных преобразований с операцией, определенной приведенной таблицей Кэли, образует абелеву группу, которая называется группой симметрий ромба.

2°. Группа самосовмещений правильного треугольника.

Д

ля заданного равностороннего треугольникаАВС рассмотрим преобра­зования, отображающие треуго- льник сам на себя:

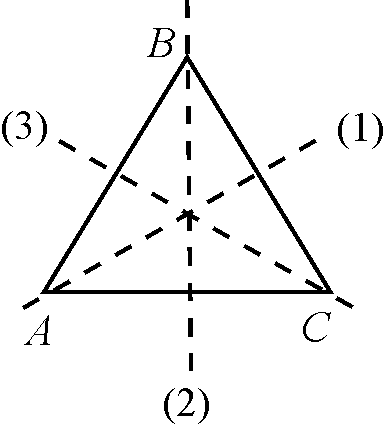
1) Е – тождественное преобразование;

2)  – поворот на угол против часовой стрелки;

3)  – поворот на угол против часовой стрелки;

4) S₁ – симметрия относительно оси (1) (В  С);

5) S₂ – симметрия относительно оси (2) (А  С);

6) S₃ – симметрия относительно оси (3) (А В).

Закон композиции определим таблицей:

I \ II	E			S1	S2	S3
E	E			S1	S2	S3
			E	S2	S3	S1
		E		S3	S1	S2
S1	S1	S2	S3	E		
S2	S2	S3	S1		E	
S3	S3	S1	S2			E

Такой закон не коммутативен. В частности, . Группа не абелева. Подмножество {Е,, } элементов данной группы образуют подгруппу (притом абелеву) группы самосовмещений, которая называется группой поворотов равностороннего треугольника.

3°. Группа перестановок. Перестановкой назовем закон, по которому элементам а, b, с, d, ... взаимно однозначно ставится в соответствие элементы того же множества, но, возможно, в другом порядке:

.

Композицией двух перестановок f₂⊙f₁ назовем последовательное приме­нение этих двух перестановок: сначала f₁, а затем f₂.

Для конечного множества Е из п элементов перестановки (или подстановки, как их иногда называют) образуют группу (не абелеву) порядка п!, которая называется симметрической груп­пой и обозначается S_n .

Иллюстрация. В группе S₄:

а) ;;f₂⊙f₁ = ⊙.

Равенство говорит о том, что перестановки f₁ и f₂ – взаимно обратные.

б) ;;f₃⊙f₄ = f₄⊙f₃ = ;

в) ;;f₅⊙f₆ = ;f₆⊙f₅ = .

Перестановки f₃ и f₄ коммутируют, а перестановки f₅ и f₆ не коммутируют.

Группу самосовмещений правильного треугольника можно представить как группу перестановок из трех элементов: ;;;;;.

Две группы G₁ и G₂ называются изоморфными, если существует взаимно однозначное соответствие f между элементами G₁ и G₂:

G₁G₂ такое, что если , тох₁+ х₂  у₁ + у₂.

Из определения изоморфных групп легко понять, что группа перестановок из трех элементов и группа самосовмещений правильного треугольника – изоморфны.

Изоморфное отображение группы G самой на себя называется авто­мор-физмом.

Def. Если Н₁ и H₂ – подмножества группы G, то произведением H₃ под­множеств Н₁ и H₂ называется: Н₃ = Н₁H₂ = {h₃h₃ = h₁h₂, h₁Н₁, h₂H₂}. Отметим, что если Н₁ и H₂ – подгруппы, то H₃, вообще говоря, не под­группа.

Если Н подгруппа G и aG, то аН и На, рассматриваемые как про­изведение множества Н и одноэлементного множества {а}, называются левым и правым смежными классами подгруппы H в G.

Свойства смежных классов (сформулированы для левых, но справед­ливы и для правых):

1°. a Н  аН  Н.

2°. а^–1bН  аН = bН (элементы а и b порождают один и тот же смежный класс, если а^–1bН). Такие элементы а и b называются эквива­лентными относительно подгруппы Н.

3°. Два смежных класса одной подгруппы H либо совпадают, либо не имеют общих элементов.

4°. aаН.

Подгруппа Н, для которой все левые смежные классы являются одновременно и пра­выми смежными классами, называется нормальным делителем группы G.

Если Н нормальный делитель группы G, то произведение смежных классов есть смежный класс.

Def. Пусть G – группа с элементами а, b, с, ... и – некоторое множество с элементами , в котором введена операция: .

Отображение f группы G на множество : f: G  называется го­моморфизмом, если a, bG выполнено f(a, b) = f(a) f(b).

при этом назы­вается гомоморфным образом группы G.

Если задано гомоморфное отображение G на , то все элементы группы G разбиваются на непересекающиеся классы; в классы объединя­ются все элементы G, которые отображаются в один и тот же элемент множества .

Т°. Гомоморфный образ группы есть группа.

Т°. Отображение f группы G на смежные классы по нормальному делителю Н при определении операции умножения классов смеж­ности как подмножеств группы G, представляет собой гомомор­физм.

Т°. Множество смежных классов группы G по нормальному дели­телю Н

с операцией умножения этих классов как подмножеств группы G образуют

группу.

Эта группа называется фактор-группой группы G по нормальному делителю Н и обозначается: G/H.

Группы линейных преобразований. Очень важными являются груп­пы различных линейных преобразований. Назовем важнейшие из таких групп:

1°. GL(n) – группа невырожденных линейных преобразований -мер­ного линейного пространстваV.

2°. О(п) – ортогональная группа или группа всех ортогональных пре­образований евклидового пространства Е_n.

3°. SO(n) – группа всех собственных ортогональных преобразований евклидового пространства Е_п.

4°. U(n) – унитарная группа или группа всех унитарных преобразова­ний унитарного пространства размерности п.