
Введение
Данные методические указания отражают многолетний опыт авторов по чтению лекций и ведению семинарских занятий по линейной алгебре на физико-техническом факультете Харьковского национального университета.
Трудно представить себе образование современного физика без знания и владения основными методами линейной алгебры. Линейной алгебре посвящена обширная литература, имеются прекрасно написанные учебники и задачники. Вместе с тем ощущается недостаток пособий, помогающих студентам выработать навыки решения задач по различным разделам линейной алгебры. Авторы данных указаний ставили перед собой цель в какой-то мере ликвидировать этот пробел.
Назначение указаний мы видим в том, чтобы активизировать самостоятельную работу студентов при изучении курса линейной алгебры, помочь активному и неформальному усвоению этого предмета.
Авторами задуман целый цикл методических указаний по различным разделам изучаемого курса «Высшая алгебра». Первой «ласточкой» в этом цикле, являются методические указания по первой части изучаемого курса «Линейные (векторные) пространства. Алгебра матриц».
Структура методических указаний подчинена решению, поставленных выше учебно-методических задач. Материал указаний разбит на четыре параграфа. В параграфе «Основные понятия и теоремы» приводятся без доказательства основные теоретические сведения (определения, теоремы, формулы), необходимые для решения задач. В параграфе «Контрольные вопросы и задания» содержатся вопросы по теории и простые задачи, решение которых не связано с большими вычислениями, но которые хорошо иллюстрируют то или иное теоретическое положение. Назначение параграфа – дать возможность студенту самому проконтролировать усвоение основных понятий. Предполагается, конечно, что основная работа над теоретическим материалом с проработкой доказательств теорем ведется по учебнику или конспекту лекций. В параграфе «Примеры решения задач» представлены решение типичных задач по изучаемой теме. Назначение параграфа «Задачи и упражнения для самостоятельной работы» отражено в его названии. Из этого раздела подбираются задачи для решения на практических занятиях, для домашних заданий по заданному разделу.
§ 1. Основные понятия и теоремы
Def:
Множество V
называется линейным (векторным)
пространством над числовым полем K,
если на множестве V
корректно*)
заданы две операции: одна внутренняя,
в дальнейшем именуемая сложением
(обозначается ![]() или
+), другая – внешняя над полем K,
в дальнейшем именуемая умножением на
скаляр (обозначается ⊙
или .),
удовлетворяющие аксиомам:
или
+), другая – внешняя над полем K,
в дальнейшем именуемая умножением на
скаляр (обозначается ⊙
или .),
удовлетворяющие аксиомам:
А. ![]()
1) ![]() ;
2)
;
2) ![]() ;
;
3) ![]() ;
4)
;
4) ![]() .
.
В. ![]() ⊙
х
⊙
х
1) 1K;
1 ⊙
x
= x
2) ![]()
⊙
(⊙
x)
= ()⊙
x.
⊙
(⊙
x)
= ()⊙
x.
С. Эти операции связаны соотношениями:
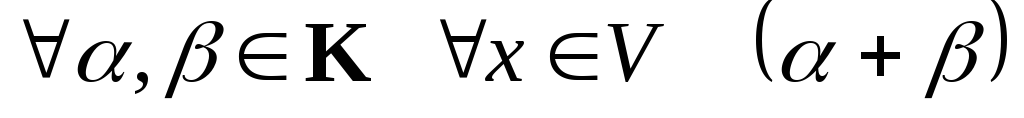 ⊙
⊙ ⊙
⊙ ⊙x;
⊙x;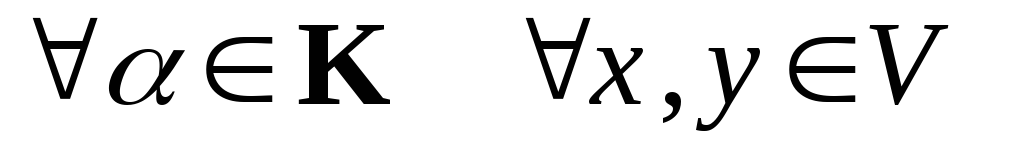
⊙
⊙ =
⊙
=
⊙ ⊙y
⊙y
Если поле K это R (поле вещественных чисел), то V называется вещественным линейным пространством. Если же поле K это С (поле комплексных чисел), то V называется комплексным линейным пространством.
Элементы линейного (векторного) пространства называются векторами.
Если множество ![]() и 1)
и 1) ![]() ,
2)
,
2) ![]()
![]() ⊙
⊙![]() ,
то множество W называется подпространством
линейного пространства V.
,
то множество W называется подпространством
линейного пространства V.
Вектор ![]() называется линейной комбинацией векторов
е1,
е2,
… , еk.
называется линейной комбинацией векторов
е1,
е2,
… , еk.
Множество
всевозможных линейных комбинаций
векторов ![]() называется линейной оболочкой этих
векторов и обозначается ℒ
называется линейной оболочкой этих
векторов и обозначается ℒ![]() .
.
Если ℒ![]() ,
то система векторов
,
то система векторов ![]() называется полной в пространстве V.
называется полной в пространстве V.
Система векторов
![]() называется линейно-независимой, если
называется линейно-независимой, если
![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() .
.
В линейном
пространстве V
система векторов ![]() называется базисом пространства V,
если система является:
называется базисом пространства V,
если система является:
а) минимальной полной в V или
б) максимальной линейно-независимой в V или
в) полной линейно-независимой в V.
Количество векторов в базисе называется размерностью пространства V и обозначается dim V.
Если в пространстве
V
задан базис ![]() ,
то
,
то ![]() такие, что
такие, что ![]() .
Такое представление называется
разложением вектора х
по базису
.
Такое представление называется
разложением вектора х
по базису ![]() ,
а числа
,
а числа ![]() – координатами вектора х
в базисе
– координатами вектора х
в базисе ![]() .
.
Два линейных
пространства V
и V
называются изоморфными, если между их
элементами установлено взаимно-однозначное
соответствие ![]() ,
причем такое, что: если
,
причем такое, что: если ![]() и
и ![]() ,
то
,
то ![]() и α ⊙
x
↔ α
⊙
x'.
и α ⊙
x
↔ α
⊙
x'.
Линейные пространства V и V изоморфны тогда и только тогда, когда dim V = dim V .
Пусть L1 и L2 – подпространства V. Тогда суммой L и пересечением N этих подпространств называются:
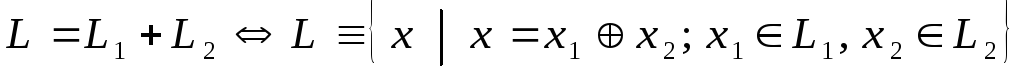 ;
;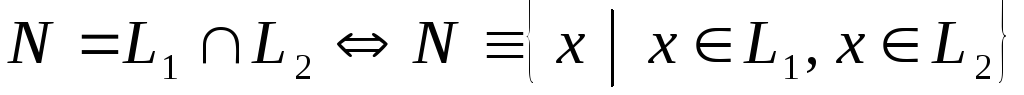
Сумма и пересечение подпространств есть подпространство.
Формула
Грасмана:
![]() .
.
Сумма L
= L1
+ L2
подпространств называется прямой суммой
(и обозначается ![]() ),
если представление
),
если представление ![]() единственно
единственно ![]() .
.
Если L – подпространство V и х0V, то множество М { x | x = х0⊕y, yL} называется линейным многообразием в V. Базис и размерность подпространства L называются базисом и размерностью линейного многообразия М, а вектор х0V называется вектором сдвига.
Если х0L (и только в этом случае) М является подпространством пространства V и при этом L М.
Def:
Линейное пространство V
над числовым полем K
называется
алгеброй если на нем корректно введена
еще одна операция (![]() или )
такая, что:
или )
такая, что:
![]() со свойствами:
со свойствами:
 ⊙
⊙ (
( ⊙
x)
⊙
x)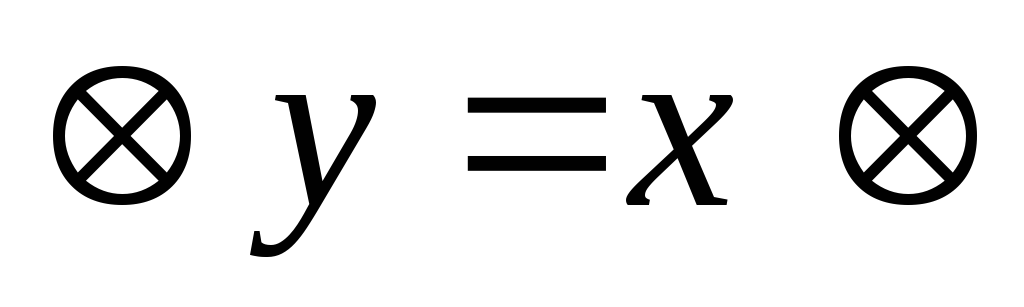 (
( ⊙ y);
⊙ y);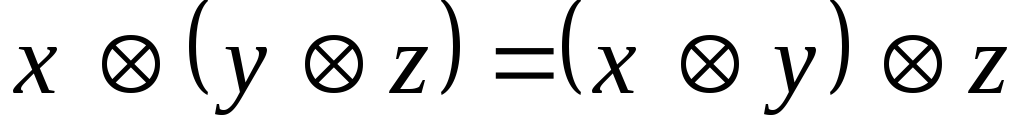 ;
;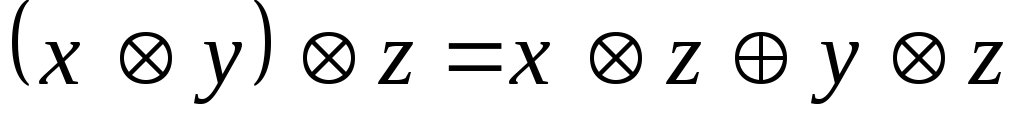 .
.
Матрицей порядка n m называется прямоугольная таблица:
 .
.
Здесь ![]() (числовое
поле) и называются элементами матрицы
А.
Другое обозначение матричных элементов
матрицы А:
(А)ij.
(числовое
поле) и называются элементами матрицы
А.
Другое обозначение матричных элементов
матрицы А:
(А)ij.
Def: Матрица А, для которой аij = aji называется симметрической, а аij = – aji называется кососимметрической (антисимметрической).
Любая квадратная матрица может быть однозначно разложена в сумму симметрической и кососимметрической матриц.
Операции над матрицами:
Умножение на скаляр из поля K: (А)ij = (Аij);
Сложение матриц одного порядка: (А + В)ij = (А)ij + (В)ij;
Умножение матриц Аn x m . Вm x k. (Вводится только для матриц у которых количество столбцов у 1ой матрицы совпадает с количеством строк у 2ой матрицы):
 .
Это правило в обиходе называют: строка
на столбец;
.
Это правило в обиходе называют: строка
на столбец;Транспонирование матрицы:
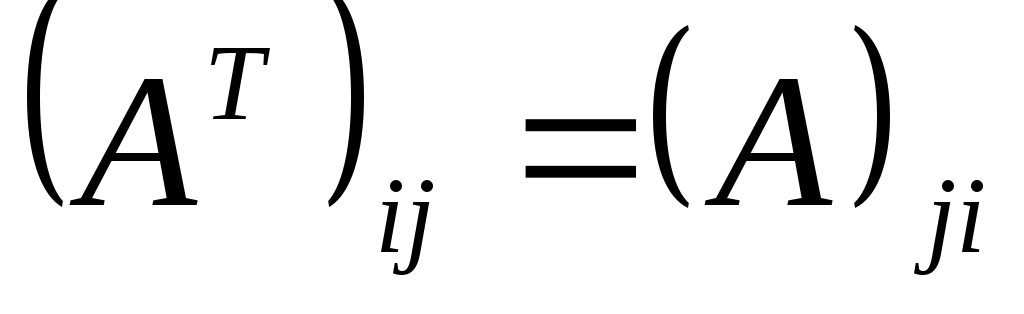 ;
;Операция комплексного сопряжения (для матриц с комплексными элементами):
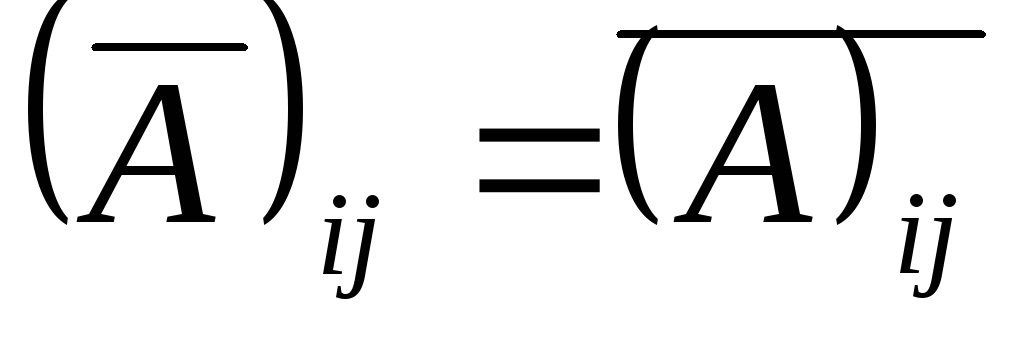 ;
;Операция эрмитового сопряжения (для матриц с комплексными элементами, обозначается * или + ):
 .
.
Нетрудно понять, что по операциям 1), 2) и 3) множество квадратных матриц (т.е. матриц порядка n x n) для заданного n образуют алгебру.
