§4. Задачи и упражнения для самостоятельной работы

1. Найти координаты вектора хв базисее₁,е₂,е₃,е₄:

а) х(1, 2, 1, 1);е₁(1, 1, 1, 1),е₂(1, 1,–1,–1),е₃(1, ­–1, 1, –1),е₄(1, –1, –1, 1);

б) х(0, 0, 0, 1);е₁(1, 1, 0, 1),е₂(2, 1, 3, 1),е₃(1, ­1, 0, 0),е₄(0, 1, –1, –1).

 а) (5, 1, –1, –1); б) (1, 0, –1, 0). 

2. Дан вектор х(1, 0, –1, 3, 8). Найти координаты этого вектора в базисе:е₁(1, 1, 1, 1, 1),е₂(0, 1, 1, 1, 1),е₃(0, ­0, 1, 1, 1),е₄(0, 0, 0, 1, 1),е₅(0, 0, 0, 0, 1).

 (1, –1, –1, 4, 5). 

3. Вектор хV_nв базисе имеет координаты (₁,₂, … ,_n). Как построить базис вV_n, чтобы координаты векторахв этом базисе были бы: (1, 0, 0, … , 0)? {₁е₁ + ₂е₂ + … + _nе_n, е₂, е₂, … е_n}. 

4. Составить формулы преобразования координат при переходе от базиса е₁,е₂,е₃,е₄ к базису . Записать матрицу переходаР_{е  е} :

а) е₁(1, 0, 0, 0),е₂(0, 1, 0, 0),е₃(0, 0, 1, 0),е₄(0, 0, 0, 1),

(1, 1, 0, 0), (1, 0, 1, 0), (1, 0, 0, 1), (1, 1, 1, 1);

б) е₁(1, 2, –1, 0),е₂(1, –1, 1, 1),е₃(–1, 2, 1, 1),е₄(–1, –1, 0, 1),

(2, 1, 0, 1), (0, 1, 2, 2), (–2, 1, 1, 2), (1, 3, 1, 2).

 a) ; б) . 

5. Проверить, что каждая из двух систем векторов является базисом и составить формулы преобразования координат при переходе от базиса ке₁,е₂,е₃,е₄. Записать матрицу переходаР_{е  е} :

а) е₁ = (1, 2, 1),е₂(2, 3, 3),е₃(3, 7, 1),

е₁(3, 1, 4),е₂(5, 2, 1),е₃(1, 1, –6);

б) е₁(1, 1, 1, 1),е₂(1, 2, 1, 1),е₃(1, 1, 2, 1),е₄(1, 3, 2, 3),

е₁(1, 0, 3, 3),е₂(–2, –3, –5, –4),е₃(2, 2, 5, 4),е₄(–2, –3, –4, –4).

 a) х₁ = –27х₁ –71х₂ – 41х₃; б) х₁ = 2х₂ + х₃ – х₄;

х₂ = 9х₁ + 20х₂ + 9х₃; х₂ = –3х₁ + х₂ – 2х₃ + х₄;

х₃= 4х₁ + 12х₂ + 8х₃; х₃ = х₁ – 2х₂ + 2х₃ – х₄;

х₄ = х₁ – х₂ + х₃ – х₄;

; . 

6. Каковы будут координаты векторов х(2, –3),у(–1, 5) в новом базисе, если векторы нового базиса выражаются через векторы старого по формулам: а) =е₂, = –е₁; б) = –е₂, =е₁.

 а) х(–3, –2), у(5, 1); б) х(3, 2), у(–5, –1). 

7. Найти матрицу перехода от базиса 1, х,х², … ,хⁿк базису 1,х–, (х–)², … , (х–)ⁿпространства полиномов степени не вышеn.

 . В этой матрице в (k +1) столбце стоят числа: (–)^k,

, 

8. Как изменится матрица линейного оператора, если в базисе е₁,е₂, …,е_nпоменять местами два вектораe_iиe_j?

 В матрице переставятся i-я и j-я строки, а также i-й и j-й столбцы. 

9. Линейные операторы АиВ вV₄имеют в базисее₁,е₂.е₃,е₄матрицы: . Каковы будут матрицы этих операторов в базисах:

а) е₁,е₃,е₂,е₄; б)е₁,е₁ + е₂,е₁+ е₂ +е₃,е₁ + е₂ +е₃ + е₄?

 а);б). 

10. Линейный оператор Азадан матрицей в базисее₁,е₂.е₃,е₄. Найти его матрицу в базисе: = е₁ +е₂ + 3е₃+е₄, = –2е₂ +е₃+е₄, = е₃+ 5е₄, =е₄. . 

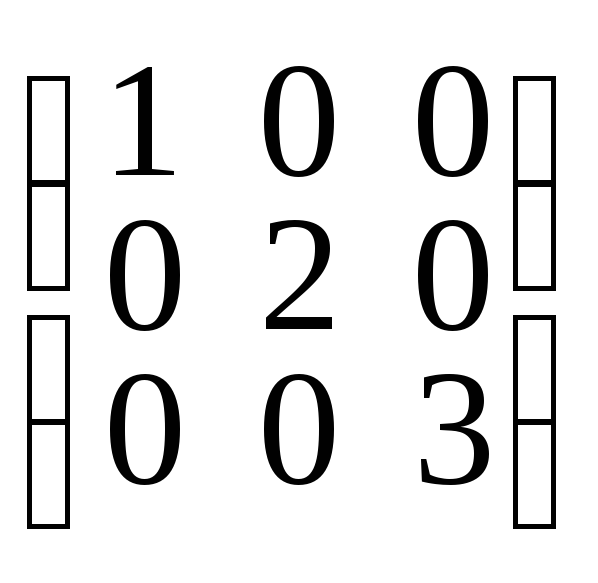
11. Линейный оператор Ав базисее₁,е₂,е₃ имеет матрицу . Найти его матрицу в базисе:f₁ = 2е₁ + 3е₂ +е₃,f₂ = 3е₁ + 4е₂+е₃,f₃ = e₁+ 2е₂+ 2е₃. . 

12. Линейный оператор Ав базисеа₁(2,–1, 0),а₂(–1, 1, –1),а₃(0,–1, 1) имеет матрицу . Найти его матрицу в базисе:b₁(1, 0, 1),b₂(0, –1, 2),b₃(1, 1, 0). . 

13. Доказать, что матрицы одного и того же линейного оператора в двух базисах совпадают тогда и только тогда, когда матрица перехода от одного из этих базисов к другому перестановочна с матрицей этого линейного оператора в одном из заданных базисов.

14. Оператор Ав базисеа₁(1, 2),а₂(2, 3) имеет матрицу . ОператорВв базисеb₁(3, 1),b₂(4, 2) имеет матрицу . Найти матрицу оператораА+Вв базисеb₁,b₂. . 

15. Найти результат последовательного выполнения линейных операций .

 Матрица преобразования будет ,

а само преобразование: . 

16. Даны матрицы операторов АиВ. Найти матрицу оператораС, еслиz=Cx,y=Ax,z=By. .

 . 

17. Оператор Ав базисеа₁(1, –2),а₂(–1, 3) имеет матрицу , а операторВв базисеb₁(2, –3),b₂(1, 2) имеет матрицу . Найти матрицу оператораАВв базисе, в котором заданы координаты всех векторов. . 

18. В базисе е₁,е₂,е₃линейная форма выражается через координаты₁,₂, ₃ векторахформулойf(x) =₁ + 2₂ + 3₃. Какой формулой выражаетсяf(x) через координатыхв базисе = е₁ +е₂, = е₂ +е₃, = е₁+е₃?

 f(x) = 4₁ + 3₂ + 5₃. 

19. В базисе {e_i}линейная формаfимеет строку коэффициентовh. Найти ее строку коэффициентовh, еслиe=Se:

а) h(1, –1, 1), ; б) h(–1, 1, 2), ;

в) h(1, 1, 1), ; г)h(1, 1, –1), .

 а) (0, 0, 2); б) (5, –5, –2); в) (3, 3, 3); г) (0, 1, 2). 

20. Дана билинейная форма А(х,у), записанная через координатыхиув базисее₁,е₂, … ,е_n. Написать эту же билинейную форму через координатыхиу в базисе , , … , .

а) А(х,у) =₁₁+ 2₁₃+ 4₂₁ + 5₂₂+ 7₂₃+₃₂+ 3₃₃,

= 2е₁ –е₂, =е₁+е₂–е₃, =е₁+ 2е₂+ 5е₃;

б) А(х,у) = 5₁₁+ 5₂₂–₁₃ –₃₁+ 2₂₃+ 2₃₂+ 5₃₃,

=е₁ , =е₁+е₂, =е₁+ 2е₂+е₃;

в) А(х,у) =₁₁+ 2₂₂ –₁₃–₃₁ + 3₂₃+ 3₃₂+ 3₃₃– 2₂₄ –2₄₂ +

+ ₃₄ +₄₃ + 4₄₄, =е₁ +е₂, =е₃+е₄, =е₂, =е₄.

 а) А(х, у) = ₁₁ – 4₁₂ –27₁₃ +6₂₁+3₂₂+43₂₃+3₃₁ –7₃₂ +194₃₃;

б) А(х, у) = 5₁₁+5₁₂+5₂₁+10₂₂+4₁₃+4₃₁ +16₂₃+16₃₂+36₃₃;

в) А(х, у) = 3₁₁+9₂₂+2₁₃+2₃₁+₂₃+₃₂+2₃₃ – 2₁₄ – 2₄₁+5₂₄+

+ 5₄₂ – 2₃₄ – 2₄₃ +4₄₄ . 

21. Как изменится матрица билинейной (квадратичной) формы, если изменить базис е₁,е₂, … ,е_nследующим образом:

а) поменять местами i^йиj^йвекторы;

б) умножить i^йбазисный вектор на0;

в) вектор е_iзаменить нае_i +е_j;

г) векторы базиса расположить в обратном порядке.

 а) поменяются местами i^я и j^я строка, а также i^й и j^й столбцы; б) i^я строка и j^й столбец

умно­жатся на  (при этом элемент диагонали, стоящий на их пересечении умножится

на ²); в) к i^й строке прибавится j^я строка, умноженная на ,а также к i^му столбцу приба-

вится j^й столбец умноженный на  (при этом элемент диагонали, стоящий на их пересе-

чении преобразуется по формуле: b_ii = b_ii +2b_ij +²b_jj); г) матрица отразится симметрич-

но относительно побочной диагонали а_{1 n}, а_{2 n–1}, … , а_{n 1}. 

22. Квадратичная форма и линейный оператор в некотором базисе имеют

одинаковые матрицы. Какой должна быть матрица Рперехода к другому

базису для того, чтобы и в другом базисе матрицы совпали?

 Р^ТР = Е – ортогональная матрица. 

23. Квадратичная форма в базисе {e_i} задана. Записать квадратичную форму в базисе {}:

а) =е₁ +е₂, = –е₁+е₂;

б) = 2е₁ –е₂, =е₁–е₂;

в) =е₁ –е₂, = е₁+ е₂;

г) =е₁+е₂+е₃, = 2е₁–е₂+е₃, = –е₁+2е₂ –3е₃.

• а) ; б) ;в) ;

г) ; 

24. Упростить уравнение кривой 2^гопорядка 9х²+24ху+16у²–40х+30у=0 и написать формулы преобразования координат.

 у² = 2х; . 

25. Привести уравнение следующих центральных поверхностей 2^гопорядка к каноническому виду и определить тип поверхности:

а) 8х² – 7у² + 8z²+ 8ху – 2хz + 8уz +1 = 0;

б) 4х² + 5у² + 6z²– 4ху +4уz = 27;

в) 2х² + 5у² + 2z²– 2ху – 4хz + 2уz = 1;

г) х² – 15у² +z²+ 12ху – 4хz + 12уz = 3.

 а) 9х² + 9у² – 9z² = –1; двуполостный гиперболоид вращения с осью Оz;

б) 2х² + 5у² + 8z² = 27; трехосный элипсоид; в)3х² + 6у² = 1; эллиптический цилиндр

с образующими параллельными оси Оz; г) 3х²+3у²–19z² = 3; однополостный

гиперболоид вращения с осью Оz. 

26. Привести уравнения следующих центральных поверхностей 2^го порядка к каноническому виду и указать преобразования координат:

а) х² + 5у² +z²+ 2ху + 6хz + 2уz = 5;

б) 2х² + 6у² + 2z²+ 8хz = 1;

в) 5х² + 8у² + 5z²+ 4ху – 8хz + 4уz = 27;

г) 6х² – 2у² + 6z²+ 4хz + 1 = 0.

 а) ; б) .

в) ; г) . 