1.6. Область пространственного заряда p-n перехода

Одномерная полупроводниковая структура с p-nпереходом представлена на рис. 6. Распределения донорови акцепторовтаковы, что в точкепроисходит изменение типа электропроводности сpнаn. Вокруг этой точки образуется двойной электрический слой, содержащий объемный заряд некомпенсированных подвижными носителями доноров и акцепторов – область пространственного заряда (ОПЗ). Внутри него существует электрическое поле напряженностьюи изменяется электрический потенциал. Их зависимости отxоднозначно определяются распределением эффективной концентрации легирующих примесей. Рассмотрим эту взаимосвязь.

Рис. 6. Одномерная полупроводниковая структура с p-n переходом

Распределение потенциала в полупроводниковой структуре с p-nпереходом описывается уравнением Пуассона, которое в одномерном случае имеет вид:

, (1.6)

в правой части которого фигурирует объемный заряд доноров и акцепторов, дырок и электронов. Получить аналитическое решение этого уравнения в случае произвольного распределения невозможно, поэтому теория полупроводниковых приборов обычно использует два приближения. Первое – приближение резкой границы ОПЗ, согласно которой существует четкая граница между ОПЗ и электронейтральными областями полупроводника. С одной стороны границы имеется объемный заряд, а с другой – электронейтральная полупроводниковая область и ее объемный заряд равен нулю (точк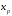иина рис. 6). Второе приближение считает, что внутри ОПЗ можно пренебречь зарядом подвижных носителей и правая часть уравнения Пуассона становится не зависящей от потенциала:

(1.7)

Вне ОПЗ из-за неоднородного легирования областей pиnтоже существует электрическое поле

(1.8)

(‘+’ для p-области, ‘-‘ дляn-области), но его напряженность обычно на порядки меньше, чем в ОПЗ. На границах ОПЗ эта напряженность имеет значения:

(1.9а)

(1.9б)

Потенциал на p-границе ОПЗ можно принять равным нулю или какому либо другому произвольному значению. Наn-границе он будет выше на величину- контактной разности потенциалов:

(1.10а)

(1.10б)

Интегрирование уравнения (1.7) с граничными условиями (1.9а) и (1.10а) позволяет получить распределение напряженности электрического поля и потенциала в ОПЗ:

(1.11)

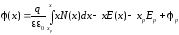(1.12)

Вне ОПЗ распределение напряженности описывается формулой (1.8), а распределение потенциала имеет вид:

(1.13)

Положение границ ОПЗ определяется из системы двух нелинейных уравнений, которая получается при подстановке (1.11) и (1.12) в граничные условия (1.9б) и (1.10б):

(1.14)

Входящие в нее выражения для зависимостей ,иприведены выше.

Система (1.14) достаточно надежно решается методом Ньютона. На рис. 7 приведены зависимости потенциала и напряженности электрического поля в полупроводниковой структуре с постоянной концентрацией доноров см^-3и гауссовым распределением акцепторовприсм^-3. Характеристическая длина= 0.76 мкм обеспечивает точку залеганияp-nперехода= 2 мкм. На рис.8 приведены распределения концентраций дырок и электронов и плотности объемного заряда в том же переходе.

а

б

Рис. 7. Распределение потенциала (а) и напряженности электрического поля (б) в p-n переходе с произвольным профилем легирующих примесей.

а

б

Рис. 8. Распределение концентраций дырок и электронов (а) и плотности объемного заряда (б) в p-n переходе с произвольным профилем легирующих примесей.

Для более простого случая p-nперехода с однородно легированными областями и ступенчатым распределением примесей (= 0):

;

;,

система уравнений (1.13) допускает аналитическое решение и приводит к известным формулам:

; ;.

Выражения (1.10) и (1.11) тоже превращаются в известные:

;

На рис. 9 представлены зависимости потенциала и напряженности электрического поля в ступенчатом p-nпереходеcN_a= 3^.10¹⁵см^-3иN_d= 10¹⁵см^-3при разных значения приложенного напряжения.