
- •Лабораторные работы. Сборник задач.
- •Оглавление
- •Часть 1. Лаборатоные работы
- •Работа со структурами и объединениями …………………………………….91
- •3 Задача
- •4 Задача
- •5 Задача
- •6 Задача
- •Дополнительное условие:использование цикла с предусловием.
- •1 Задача
- •2 Задача
- •Дополнительное условие: программа написана без использования функции.
- •Дополнительное условие: программа написана с использованием функций.
- •3 Задача
- •Дополнительное условие: программа написана без использования функции.
- •Дополнительное условие: программа написана с использованием функции.
- •4 Задача
- •Дополнительное условие: программа написана без использования функции
- •Дополнительное условие: программа написана с использованием функции.
- •Самостоятельная работа
- •Лабораторная работа №3
- •Самостоятельная работа
- •1 Задача
- •2 Задача
- •1 Задача
- •2 Задача
- •3 Задача
- •Лабораторная работа №6
- •1 Задача
- •1 Задача
- •2 Задача
- •3 Задача
- •1 Задача
- •1 Задача
- •2 Задача
- •3 Задача
- •4 Задача
- •Синтаксический анализатор
- •Самостоятельная работа
- •1 Задача
- •2 Задача
- •3 Задача
- •Работа с каталогами
- •Самостоятельная работа
- •1 Задача
- •2 Задача
- •1 Задача
- •2 Задача
- •3 Задача
- •1 Задача
- •2 Задача
- •1 Задача Реализовать очередь, состоящую из целых чисел
- •Комментарий:
- •2 Задача
- •1 Задача
- •Идеально-сбалансированные деревья
- •1 Задача
- •2 Задача
- •1 Задача
- •2 Задача
- •3 Задача
- •1 Задача
- •2 Задача
- •3 Задача
- •1 Задача
- •1 Задача
- •1 Уровень сложности
- •2 Уровень сложности
- •3 Уровень сложности
- •1 Уровень сложности.
- •2 Уровень сложности
- •3 Уровень сложности
- •1 Уровень сложности
- •Работа с несколькими массивами
- •Преобразование массива
- •Изменение элементов массива
- •2 Уровень сложности Формирование массива и вывод его элементов
- •Анализ элементов массива
- •Преобразование массива
- •Изменение элементов массива
- •Удаление и вставка элементов
- •Серии целых чисел
- •3 Уровень сложности Множества точек на плоскости
- •1 Уровень сложности
- •2 Уровень сложности
- •3 Уровень сложности
- •1 Уровень сложности
- •2 Уровень сложности
- •3 Уровень сложности
- •1 Уровень сложности
- •2 Уровень сложности
- •3 Уровень сложности
- •Not простое_логическое
- •(Простое_логическое знак_операции простое_логическое)
- •Построить синтаксический анализатор для понятия предложение.
- •1 Уровень сложности
- •2 Уровень сложности
- •1 Уровень сложности
- •Примеры:
- •Двусвязные списки
- •1 Уровень сложности
- •2 Уровень сложности
- •3 Уровень сложности
3 Уровень сложности
Получить последовательность dk,dk-1,…,d0десятичных цифр числа2200, т. е. такую целочисленную последовательность, в которой каждый член diудовлетворяет условию0≤di≤9 и, дополнительно, dk*10k+dk-1*10k-1+…+d0= 2200.
Получить последовательность d-1,d-2,…,d-kдесятичных цифр числа 2-200, т. е. такую целочисленную последовательность, в которой каждый член diудовлетворяет условию0≤di≤9 и, дополнительно, d-1*10-1+d-2*10-2+…+d-k*10-k=2-200.
Получить последовательность dk, dk-1,…,d0десятичных цифр числа 100!, т. е. такую целочисленную последовательность, в которой каждый член diудовлетворяет условию0≤di≤9 и, дополнительно, dk10k+dk-110k-1+…+d0= 100!
Дано натуральное количество n (n≥5). Получить все пятерки натуральных чисел x1, x2, x3, x4, x5такие, что x1≥x2≥x3≥x4≥x5и x1+…+x5= n.
Дано натуральное число m. Вставить между некоторыми цифрами 1, 2, 3, 4, 5, 6, 7, 8, 9, записанными именно в таком порядке, знаки +, - так, чтобы значением получившегося выражения было число m. Например, если m = 122, то подойдет следующая расстановка знаков: 12+34–5–6+78+9. Если требуемая расстановка знаков невозможна, то сообщить об этом.
Даны одновременно не равные 0 целые f и g. Найти НОД(|f|,|g|) и целые u, v такие, что fu+gv=НОД (|f|,|g|).
Даны целые k, l, m такие, что k и l одновременно не равны 0, а m делится на НОД(|f|,|g|). Найти какое-нибудь целочисленное решение уравнения kx+ly=m.
Показать, что если x1, y1и x2, y2– два целочисленных решения уравнения kx+ly=m, то x1–x2, y1–y2– целочисленное решение уравнения kx+ly=0. Вывести отсюда, что если ¯x,¯y – какое-нибудь целочисленное решение уравнения kx+ly=m, то все целочисленные решения этого уравнения описываются формуламиx=¯x + l’t,y=¯y – k’t, где k’ = k/НОД(k,l), l’ = l/НОД(k,l) (t=0, ±1, ±2,…).
Написать программу, которая позволяет проверить, обладает ли уравнение kx + ly = m решением в целых неотрицательных числах, и если обладает, то позволяет построить какое-то одно такое решение.
Даны натуральные взаимно простые числа n, p. Используя алгоритм (Даны одновременно не равные 0 целые f и g. Найти НОД(|f|,|g|) и целые u, v такие, что fu+gv = НОД (|f|,|g|).) найти натуральное m такое, что, во-первых, m < p и, во-вторых, nm при делении на p дает остаток 1.
Дано натуральное число k и одновременно не равные 0 целые числа n1,…,nk. Найти НОД(|n1|,…,|nk|) и целые u1,…,ukтакие, что u1n1+…+uknk= НОД(|n1|,…,|nk|).
Даны натуральные числа a1,…,a10. Предположим, что имеется десять видов монет достоинством a1,…,a10. Обозначим через bkчисло решений уравнения a1x1+…+a10x10= k, где xiможет принимать целые неотрицательные значения. Получить b0,…,b20.
Дано натуральное число n. Как наименьшим количеством монет можно выплатить n копеек? Предполагается, что в достаточно большом количестве имеются монеты достоинством в 1, 2, 3, 5, 10, 15, 20 и 50 коп.
Дано четное число n>2. Проверить для этого числа гипотезу Гольдбаха. Эта гипотеза (на сегодняшний день не опровергнутая и полностью не доказанная) заключается в том, что каждое четное n, большее двух, представляется в виде суммы двух простых чисел.
Известно, что любое натуральное число можно представить в виде суммы не более чем четырех квадратов натуральных чисел или, что то же самое, в виде суммы четырех квадратов неотрицательных целых чисел (теорема Лагранжа). Дано натуральное n. Указать такие неотрицательные целые числа x, y, z, t, что n = x
 + y
+ y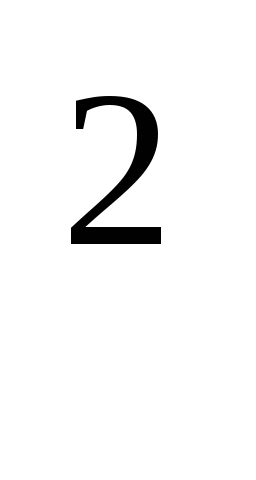 + z
+ z + t
+ t .
.Дано число 14567 в 5-ричной системе счисления и число 10101 в двоичной системе счисления. Необходимо подсчитать сумму этих двух чисел. Сумму вывести в 9-ричной системе счисления.
Дано число 3214 в 8-ричной системе счисления и число 123 в 3-ичной системе счисления. Необходимо найти разность этих чисел. Результат разности вывести в 7-ричной системе счисления.
Получить последовательность dk, dk-1,…,d0десятичных цифр числа:
100!+2100;
100!–2100, т. е. такую целочисленную последовательность, в которой каждый член diудовлетворяет условию0≤di≤9 и, дополнительно, dk10k+dk-110k-1+…+d0равно 1000!+2100или соответственно 100!–2100.
Даны действительное число x, натуральное число q (0≤x<1,q≥2). Получить пять цифр q-ичного представления числа x, т. е. получить последовательность целых неотрицательных a-1,…,а-5такую, что x = a-1q-1+…+a-5q-5+r,0≤ai≤q-1,r<q-5.
Дано натуральное число p. Получить последовательность a0,…,an, каждый член которой равен -1, 0 или 1, такую, что p = an3n+…+a13+a0(an≠0).
Даны натуральное число n, целые числа a0,…,anтакие, что каждое aiравно нулю или единице и an≠0. Последовательность a0,…,anзадает двоичное представление некоторого целого числаp=an2n+…+a12+a0. Получить последовательность нулей и единиц, задающую двоичное представление:
числа p+1;
числа p–1;
числа 3p.
Ряды
