
- •Лабораторные работы. Сборник задач.
- •Оглавление
- •Часть 1. Лаборатоные работы
- •Работа со структурами и объединениями …………………………………….91
- •3 Задача
- •4 Задача
- •5 Задача
- •6 Задача
- •Дополнительное условие:использование цикла с предусловием.
- •1 Задача
- •2 Задача
- •Дополнительное условие: программа написана без использования функции.
- •Дополнительное условие: программа написана с использованием функций.
- •3 Задача
- •Дополнительное условие: программа написана без использования функции.
- •Дополнительное условие: программа написана с использованием функции.
- •4 Задача
- •Дополнительное условие: программа написана без использования функции
- •Дополнительное условие: программа написана с использованием функции.
- •Самостоятельная работа
- •Лабораторная работа №3
- •Самостоятельная работа
- •1 Задача
- •2 Задача
- •1 Задача
- •2 Задача
- •3 Задача
- •Лабораторная работа №6
- •1 Задача
- •1 Задача
- •2 Задача
- •3 Задача
- •1 Задача
- •1 Задача
- •2 Задача
- •3 Задача
- •4 Задача
- •Синтаксический анализатор
- •Самостоятельная работа
- •1 Задача
- •2 Задача
- •3 Задача
- •Работа с каталогами
- •Самостоятельная работа
- •1 Задача
- •2 Задача
- •1 Задача
- •2 Задача
- •3 Задача
- •1 Задача
- •2 Задача
- •1 Задача Реализовать очередь, состоящую из целых чисел
- •Комментарий:
- •2 Задача
- •1 Задача
- •Идеально-сбалансированные деревья
- •1 Задача
- •2 Задача
- •1 Задача
- •2 Задача
- •3 Задача
- •1 Задача
- •2 Задача
- •3 Задача
- •1 Задача
- •1 Задача
- •1 Уровень сложности
- •2 Уровень сложности
- •3 Уровень сложности
- •1 Уровень сложности.
- •2 Уровень сложности
- •3 Уровень сложности
- •1 Уровень сложности
- •Работа с несколькими массивами
- •Преобразование массива
- •Изменение элементов массива
- •2 Уровень сложности Формирование массива и вывод его элементов
- •Анализ элементов массива
- •Преобразование массива
- •Изменение элементов массива
- •Удаление и вставка элементов
- •Серии целых чисел
- •3 Уровень сложности Множества точек на плоскости
- •1 Уровень сложности
- •2 Уровень сложности
- •3 Уровень сложности
- •1 Уровень сложности
- •2 Уровень сложности
- •3 Уровень сложности
- •1 Уровень сложности
- •2 Уровень сложности
- •3 Уровень сложности
- •Not простое_логическое
- •(Простое_логическое знак_операции простое_логическое)
- •Построить синтаксический анализатор для понятия предложение.
- •1 Уровень сложности
- •2 Уровень сложности
- •1 Уровень сложности
- •Примеры:
- •Двусвязные списки
- •1 Уровень сложности
- •2 Уровень сложности
- •3 Уровень сложности
2 Уровень сложности
Дано натуральное число n. Проверить, является ли это число палиндромом.
Найти все натуральные числа, не превосходящие заданного N и делящиеся на каждую из своих цифр.
Найти все натуральные числа, не превосходящие заданного N и равные сумме кубов своих цифр.
Даны натуральные числа m и n. Получить все меньшие n натуральные числа, квадрат суммы цифр которых равен m.
Дано натуральное число n. Среди чисел 1,2,…,n, найти автоморфные, т. е. такие, запись которых совпадает с последними цифрами записи их квадрата (6
 = 36, 25
= 36, 25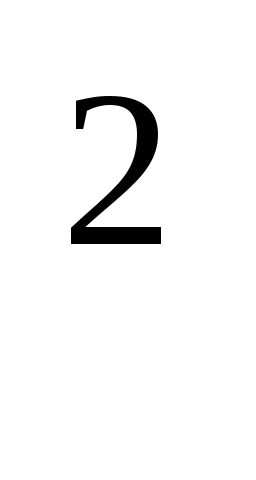 = 625).
= 625).Найти натуральное число из интервала [1, n] с максимальной суммой делителей.
Даны целые числа p и q . Получить все взаимнопростые с p делители числа q.
Два натуральных числа называют дружественными, если каждое из них равно сумме всех делителей другого, кроме самого этого числа . Найти все пары дружественных чисел, лежащих в диапазоне от А до В.
Натуральное число называется совершенным, если оно равно сумме всех своих делителей, за исключением самого себя.
Число 6 совершенное, т.к. 6 = 1 + 2 + 3
Число 8 не совершенное, т.к. 8
 1 + 2 + 4
1 + 2 + 4
Дано натуральное n. Получить все совершенные числа, меньше n.
Даны натуральные числа m и n . Получить все их натуральные общие кратные, меньшие m*n .
Дано натуральное число n. Выяснить, имеются ли среди чисел n,n+1,…,2n близнецы, т. е. простые числа, разность между которыми равна двум.
Напечатать все представления натурального числа N суммой натуральных чисел. Перестановка слагаемых нового способа не дает.
Напечатать все представления заданного натурального числа N в виде суммы не менее двух попарно различных положительных слагаемых. Перестановка слагаемых нового способа не дает.
Дано натуральное число N (N
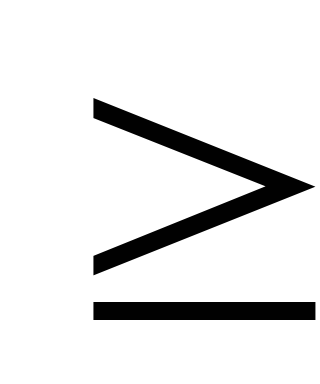 3).
Получить все тройки натуральных чисел
x1,x2,x3
такие, что x1
3).
Получить все тройки натуральных чисел
x1,x2,x3
такие, что x1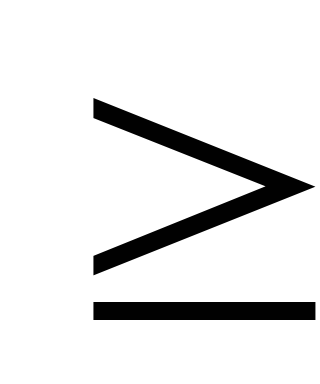 х2
х2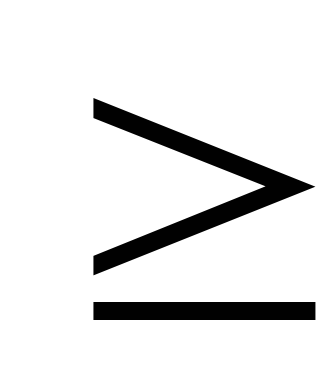 x3 и x1+x2+x3=n.
x3 и x1+x2+x3=n.Дано натуральное число N. Получить все Пифагоровы тройки натуральных чисел, каждое из которых не превосходит n, т. е. все такие тройки натуральных чисел a, b, c, что a
 +b
+b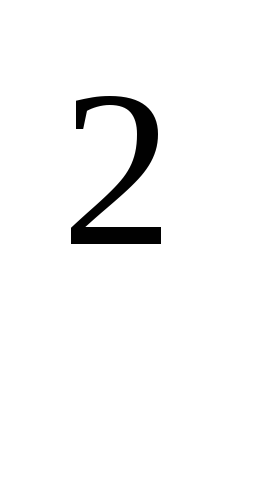 = c
= c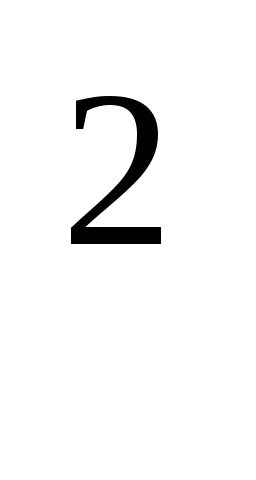 (a
(a b
b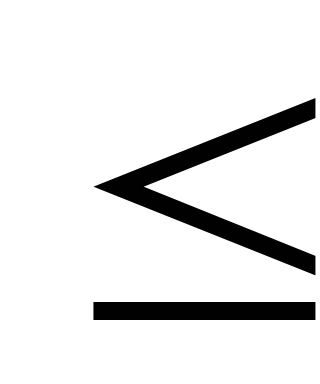 c
c N).
N).Дано натуральное число N. Можно ли представить его в виде суммы двух квадратов натуральных чисел. Если можно, то:
указать пару x, y таких натуральных чисел, что N=x
 +y
+y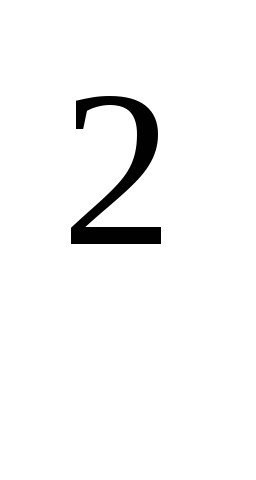 ;
;указать все пары таких натуральных чисел, что N=x
 +y
+y , x
, x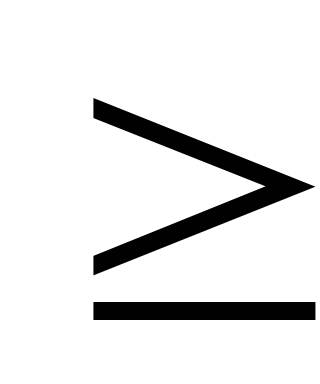 y.
y.
Дано натуральное
число N. Можно ли представить его в виде
суммы трех квадратов натуральных чисел?
Если можно, то указать тройку x, y, z таких
натуральных чисел, что N=x![]() +y
+y![]() +z
+z![]() .
.
Найти все натуральные числа, не превосходящие заданного N и представимые в виде суммы квадратов двух каких-либо различных натуральных чисел.
Найти все способы
представления заданного натурального
числа N в виде суммы двух кубов натуральных
чисел: N = i3 + j3(i![]() j).
j).
Найти наименьшее
натуральное число N, представимое двумя
различными способами в виде суммы кубов
двух натуральных чисел: N = x3 + y3
(x![]() y).
y).
Определить, можно ли представить заданное натуральное число как сумму кубов каких-либо трех натуральных чисел.
Найти минимальное число, которое представляется суммой четырех квадратов натуральных чисел не единственным образом.
Для заданного
натурального N определить наименьшее
число S, которое можно представить в
виде суммы a![]() +b
+b![]() по крайней мере двумя различными
способами (a, b – натуральные числа;
представления, отличающиеся лишь
порядком слагаемых, различными не
считаются).
по крайней мере двумя различными
способами (a, b – натуральные числа;
представления, отличающиеся лишь
порядком слагаемых, различными не
считаются).
В качестве основания
позиционной системы может быть взято
отрицательное целое число. Например,
можно рассмотреть систему с основанием
–10 . Любое целое n единственным образом
представляется в виде суммы
a![]() (-10)
(-10)![]() +a
+a![]() (-10)
(-10)![]() +…+a
+…+a![]() (-10)+a
(-10)+a![]() ,
где0
,
где0![]() a
a![]()
![]() 9,i=0,…,s.
Из сказанного следует, что любое целое
n записывается в системе с основанием
–10 в виде целого числа без знака
a
9,i=0,…,s.
Из сказанного следует, что любое целое
n записывается в системе с основанием
–10 в виде целого числа без знака
a![]() a
a![]() …a
…a![]() a
a![]() .
Дано целое n. Построить представление
n в системе с основанием –10, т.е. найти
соответствующие a
.
Дано целое n. Построить представление
n в системе с основанием –10, т.е. найти
соответствующие a![]() a
a![]() …a
…a![]() a
a![]() .
.
Найти все натуральные числа, не превосходящие заданного N, десятичная запись которых есть строго возрастающая (строго убывающая) последовательность цифр.
Получить все меньшие 106натуральные числа, которые являются палиндромами как в десятичной, так и в двоичной системах.
Дано натуральное число m. Найти такое натуральное n, что двоичная запись n получается из двоичной записи m изменением порядка цифр на обратный (m задано в десятичной системе, и n надо также получить в десятичной системе, например, для m=6 получаетсяn=3).
Дано натуральное число n. Требуется получить последовательность, которая состоит из нулей и семерок и образует десятичную запись некоторого натурального числа, делящегося на n.
(Воспользоваться тем, что в числовой последовательности 7, 77, 777,… обязательно найдутся два члена, дающие при делении на n один и тот же остаток.)
Дано натуральное число m (m<27). Получить все трехзначные натуральные числа, сумма цифр которых равна m.
Вводится последовательность из nцелых чисел. Найти сумму 3-х наибольших чисел. Эту задачу необходимо решить без использования массива.
Дано натуральное число n. Найти все меньшие n числа Мерсена. (Простое число называется числом Мерсена, если оно может быть представлено в виде 2p–1, где p – тоже простое число).
Натуральное число из n цифр является числом Армстронга, если сумма его цифр, возведенных в n-ю степень, равна самому числу (как, например, 153 = 13+53+33). Получить все числа Армстронга, состоящие из двух, трех и четырех цифр.
Найти все простые несократимые дроби, заключенные между 0 и 1, знаменатели которых не превышают 7 (дробь задается двумя натуральными числами – числителем и знаменателем).
Дано натуральное число n. Выяснить, можно ли представить n! в виде произведения трех последовательных целых чисел.
Дано натуральное число n (n≤ 99). Получить все способы выплаты суммы n с помощью монет достоинством 1, 5, 10 и 20 коп.
Назовем натуральное число палиндромом, если его запись читается одинаково с начала и с конца (как, например, 4884, 393, 1 и т. д.). Найти все меньшие 100 натуральные числа, которые при возведении в квадрат даю палиндром.
Рассмотрим некоторое натуральное число n. Если это не палиндром, то изменим порядок его цифр на обратный и сложим исходное число с получившимся. Если сумма не палиндром, то над ней повторяется то же действие и т. д., пока не получится палиндром. (Неизвестно, завершится ли этот процесс для любого натурального n). Даны натуральные k, l, m (k
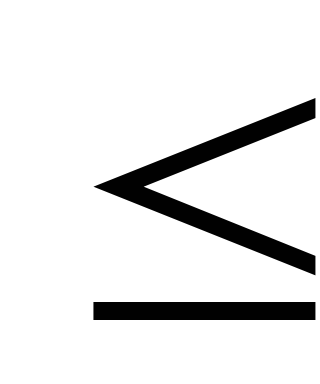 l). Проверить, верно ли, что для любого
натурального числа из диапазона [k,l],
процесс завершится не позднее, чем
после m таких действий.
l). Проверить, верно ли, что для любого
натурального числа из диапазона [k,l],
процесс завершится не позднее, чем
после m таких действий.Рассмотрим некоторое натуральное число n (n>1). Если оно четное, то разделим его на 2, иначе умножим на 3 и прибавим 1. Если полученное число не равно 1, то повторяется, то же действие и т. д., пока не получится 1. (Неизвестно, завершится ли этот процесс для любогоn>1). Даны натуральные числа k, l, m (1<k
 l). Проверить, верно ли, что для любого
натурального n из диапазона [k, l] процесс
завершится не позднее, чем после m таких
действий.
l). Проверить, верно ли, что для любого
натурального n из диапазона [k, l] процесс
завершится не позднее, чем после m таких
действий.Алгоритм Евклида (нахождения наибольшего общего делителя (НОД) неотрицательных целых чисел) основан на следующих свойствах этой величины. Пусть m и n – одновременно не равные нулю целые неотрицательные числа и пусть m ≥ n. Тогда, если n = 0, то НОД(n, m) = m, а если n≠0, то для чисел m, n и r (r – остаток от деления m на n) выполняется равенство: НОД(m,n) = НОД(n,r). Например, НОД(15, 6) = НОД(6, 3) = НОД(3, 0) = 3) допускает многочисленные обобщения. Например, вместе с НОД(f, g) можно вычислять целые u и v такие, что fu+fv = НОД(f, g).
