Замечание 1. Если функция f(x) интегрируема на отрезке с концами a, b, то справедливо неравенство
|
b f(x) dx |
≤ |
|
b |
|
Z |
|
Z |
|||
a |
|
|
a |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|f(x)| dx .
Замечание 2. Если функция f(x) непрерывна на [a, b], f(x) ≥ 0 на
Zb
[a, b] и x0 [a, b] : f(x0) > 0, то f(x) dx > 0.
a
1.6 Интегрируемость кусочно непрерывной функции
Рассмотрим класс интегрируемых функций, более широкий по сравнению с классом непрерывных функций. Для этого потребуется следующая лемма, указывающая еще одно достаточное условие интегрируемости функции.
Лемма 1.3. Пусть функция f(x) интегрируема на отрезке [a, b]. Изменение значения функции в конечном числе точек не влияет на ее интегрируемость на [a, b] и на величину интеграла.
1) Если f(x) = 0 на |
[a, b], |
то |
f R[a,b] и I(f) = |
Zb f(x) dx |
= 0. |
|
|
|
|
a |
и |
Измененим значение этой функции в одной точке. Пусть α [a, b] |
|||||
f(x) = |
0, x [a, b] \ {α}, |
|
|
||
e |
|
A, |
x = α. |
|
|
|
|
|
|
|
|
Пусть, для определенности, A > 0. Зафиксируем ε > 0 и выберем
ε
произвольное разбиение τ = {xk}nk=0 N[a, b] с диаметром d(τ) < 2A. Точка α может принадлежать только одному отрезку разбиения, если α не является точкой из разбиения τ, или двум отрезкам, если α является точкой из разбиения τ, не совпадающей с a или b. В любом случае
Sfe(τ) < 2A · |
ε |
= ε, sfe(τ) = 0, |
2A |
и потому Sfe(τ) − sfe(τ)f |
< ε. Из пункта 3) теоремы 1.9 следует, что f |
||||
|
. А так как |
lim |
s |
(τ) = 0, |
то из пункта 2) теоремы 1.9 следует, что |
R[a,b] |
|
e |
|||
|
|
e |
|
||
Zb
I(fe) = fe(x) dx = 0.
a
22
2) Пусть f R[a,b],
f(x) = |
f(x), |
x [a, b] \ {α}, |
|
e |
|
A, |
x = α, |
|
|
|
|
0, x [a, b] \ {α},
иg(x) = A − f(α), x = α.
(1.21)
Тогда fe(x) = f(x) + g(x), x [a, b], и по теореме 1.12 функция fe интегрируема на [a, b], при этом
Zb f(x) dx = |
Zb f(x) dx + Zb g(x) dx = |
Zb f(x) dx. |
||
a |
e |
a |
a |
a |
Если изменение значения функции происходит в конечном числе точек отрезка [a, b], то для каждой такой точки следует построить функцию, аналогичную функции g, которая будет интегрируема на [a, b], составить сумму, аналогичную (1.21), и применить теорему 1.12.
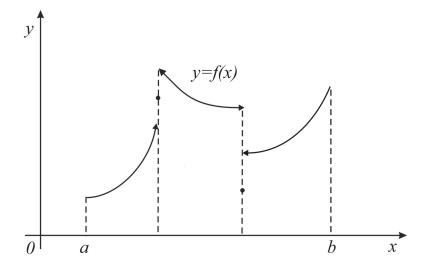
Определение 1.6. Функция f :
непрерывной на отрезке [a, b], если ключением конечного числа точек, разрыва первого рода.
[a, b] → R называется кусочно она непрерывна на [a, b] за искоторые являются ее точками
Рис. 1.1: Пример кусочно непрерывной функции
Теперь мы можем доказать результат, расширяющий класс интегрируемых по Риману функций.
Теорема 1.19. Если функция f : [a, b] → R кусочно непрерывна на отрезке [a, b], то она интегрируема на нем.
Рассмотрим случай, когда функция f(x) имеет на отрезке [a, b] одну точку разрыва первого рода c (a, b), то есть существуют конечные
23
предельные значения f(c + 0) и f(c − 0). Рассмотрим функции
f1(x) = |
|
f(x), x [a, c), |
и f2(x) = |
|
f(x), x (c, b], |
||
|
f(c |
− |
0), x = c, |
|
f(c + 0), x = c. |
||
|
|
|
|
|
|
|
|
Так как функции f1(x) и f2(x) непрерывны на отрезках [a, c] и [c, b] соответственно, то они интегрируемы на этих отрезках. Тогда по лемме 1.3 функция f(x), отличающаяся от функции f1(x) значением в одной точке, интегрируема на отрезке [a, c]. Аналогично, f(x) интегрируема и на отрезке [c, b]. Тогда по теореме 1.17 f(x) интегрируема на [a, b].
Замечание. Если функция f(x) кусочно непрерывна на отрезке [a, b], то она интегрируема на нем и для вычисления определенного интеграла от такой функции отрезок [a, b] разбивается на конечное число отрезков [ak, bk] так, что f(x) является непрерывной и ограниченной функцией на интервалах (ak, bk).
1.7Первая интегральная теорема о среднем
Теорема 1.20. Пусть функции f и g удовлетворяют условиям:
1) f и g интегрируемы на отрезке [a, b]; |
|
|
|
2) |
числа m и M такие, что m ≤ f(x) ≤ M, |
x [a, b]; |
|
3) |
функция g не меняет знак на отрезке [a, b], то есть |
|
|
|
g(x) ≥ 0, x [a, b], или g(x) ≤ 0, x [a, b]. |
|
|
Тогда |
|
|
|
|
µ [m, M] : Zb f(x)g(x) dx = µ Zb g(x) dx. |
(1.22) |
|
|
a |
a |
|
Пусть, например, g(x) ≥ 0, x [a, b], тогда из условия 2) следует, что mg(x) ≤ f(x)g(x) ≤ Mg(x), x [a, b]. Так как функции f и g
интегрируемы на отрезке [a, b], то функция f · g также интегрируема на этом отрезке и в силу теоремы 1.18
m Zb g(x) dx ≤ Zb f(x)g(x) dx ≤ M Zb g(x) dx. |
(1.23) |
||
a |
a |
a |
|
Если Zb g(x) dx = 0, то из (1.23) следует, что |
Zb f(x)g(x) dx = 0, и в этом |
||
a |
|
a |
|
случае равенство (1.22) выполняется при любом µ.
24
Если же Zb g(x) dx 6= 0, то |
Zb g(x) dx > 0. Поэтому неравенство (1.23) |
||||
a |
a |
|
|
|
|
равносильно неравенству |
|
|
|
|
|
|
Zb f(x)g(x) dx |
||||
m ≤ µ ≤ M, где µ = |
a |
|
|
. |
|
|
b |
|
|||
|
|
|
Z |
g(x) dx |
|
a
Из определения µ следует равенство (1.22). Аналогично доказывается теорема и в случае, когда g(x) ≤ 0 на [a, b].
Cледствие 1. Если функция f интегрируема на отрезке [a, b] и m ≤ f(x) ≤ M, x [a, b], то
Zb
µ [m, M] : f(x) dx = µ(b − a).
a
Cледствие 2. Если функция f(x) непрерывна на отрезке [a, b], а функция g(x) интегрируема и не меняет на нем знак, то
c [a, b] : |
Zb f(x)g(x) dx = f(c) Zb g(x) dx. |
(1.24) |
|
|
a |
a |
|
В частности, если g(x) ≡ 1 на [a, b], то |
|
||
c [a, b] : |
Zb f(x) dx = f(c)(b − a). |
(1.25) |
|
|
|
a |
|
Из непрерывности функции f(x) на отрезке [a, b] следует, что она интегрируема на нем. Согласно второй теореме Вейерштрасса
p, q |
a, b |
f p |
max f(x) = Mf , |
f(q) = min f(x) = mf , |
|
|
[ |
] : ( |
|
[a,b] |
|
) = x |
x [a,b] |
||||
то есть mf ≤ f(x) ≤ Mf , x [a, b]. Все условия теоремы 1.20 выполнены, поэтому
µ [mf , Mf ] : |
Zb f(x)g(x) dx = µ Zb g(x) dx. |
|
|
a |
a |
По теореме Больцано–Коши о промежуточном значении непрерывной на отрезке функции, существует точка c, принадлежащая отрезку с концами в точках p и q, а значит, c [a, b], такая, что f(c) = µ. Таким образом,
c [a, b] : |
Zb f(x)g(x) dx = f(c) Zb g(x) dx. |
|
|
a |
a |
25