Electrodynamics

значению интеграла, именно эта функция определяет классическую траекторию физической системы.

Рассмотрим изменение интеграла действия при малых изменениях функций q t :

Поскольку принцип наименьшего действия формулируется в предположении, что моменты времени t1 и t2 координаты системы фиксированы (см. (2.35)), то

q t1 0, q t2 0 , (2.38)

и внеинтегральный член в (2.37) обращается в 0. Необходимым условием экстремальности функционала действия является обращение в 0 его первой вариа-

В теории поля в качестве обобщенных координат выступают полевые переменные, зависящие не только от времени, но и от пространственных переменных. Покажем, что уравнения электромагнитного поля получаются в результате варьирования действия

Здесь интеграл берется по всему пространству и по отрезку времени, ограниченному моментами t1 и t2 . Интеграл действия (2.40) состоит из двух частей: член, описывающий свободное электромагнитное поле (в отсутствие зарядов)

Мы знаем, что интеграл по объему от дивергенции векторного поля в трехмерном пространстве может быть преобразован по теореме Остроградского – Гаусса в интеграл по поверхности, охватывающей этот объем. Теорема Остроград-

34

ского – Гаусса может быть обобщена на случай четырехмерного пространствавремени:

где dS – элемент гиперповерхности в четырехмерном пространстве-времени.

В нашем случае

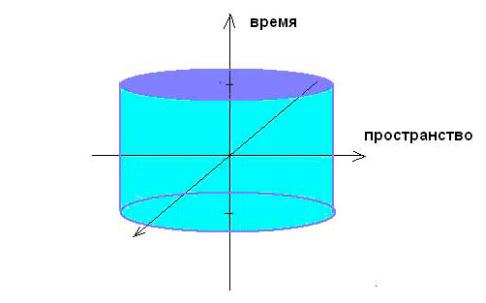
Поверхность в пространстве-времени должна быть выбрана следующим образом. Она должна состоять из двух гиперплоскостей S1 и S2 , которые представляют все пространство в моменты времени t1 и t2 , и "боковой" поверхности четырехмерного цилиндра (см. рис. 1).

(аналогично тому, как это имело место для координат механической системы, см. (2.38)). Поскольку полная гиперповерхность должна охватывать все трехмерное пространство в моменты времени между t1 и t2 , "боковую" часть гипер-

35

совпадает с четвертым уравнением Максвелла (1.17).

Таким образом, мы получили четыре уравнения для четырех компонент поля A . Что касается первого и второго уравнений Максвелла, их можно рассматривать как следствие связи между потенциалами и напряженностями поля (2.5), (2.2). В самом деле, мы получили связь между напряженностью магнитного поля H и векторным потенциалом A как следствие второго уравнения Максвелла, а связь между напряженностью электрического поля E и скалярным и векторным потенциалами – как следствие первого уравнения Максвелла. Об-

получаем первое уравнение Максвелла (1.56). Беря дивергенцию от обеих частей уравнения (2.2),

Он является антисимметричным по всем своим индексам вследствие антисим-

содержат первое и второе уравнения Максвелла. В этом легко убедиться, расписав уравнения (2.64) по компонентам, как это было сделано выше для уравнений (2.50). В силу антисимметричности отличны от нуля только те компоненты тензора A , у которых индексы , , принимают различные значе-

ния. Таких комбинаций индексов , , всего четыре, поэтому запись (2.64) содержит четыре скалярных уравнения. Уравнения (2.64) можно записать еще в одной форме, введя единичный абсолютно антисимметричный псевдотензор

Последнее выражение имеет один свободный индекс, , что делает совершенно очевидным тот факт, что (2.66) содержит четыре независимых уравнения.

2.4. Теорема единственности для системы уравнений Максвелла.

Итак, мы имеем два представления уравнений электромагнитного поля: либо через напряженности, либо через потенциалы поля. Система уравнений Максвелла (1.1) – система дифференциальных уравнений в частных производных первого порядка относительно полевых переменных (напряженностей). Можно доказать так называемую теорему единственности для системы уравнений Максвелла:

Пусть заданы источники поля – функции r, t и j r, t в произвольный

V, а на поверхности S этого объема заданы граничные условия – компоненты одного из векторов E r, t S или H r, t S в произвольный момент вре-

мени. При этих условиях решение уравнений Максвелла внутри объема V единственно.

38

Доказательство теоремы проводится от противного и не представляет сложностей. Предположим, что существуют два различные решения системы

Воспользуемся уравнением баланса энергии (1.77), которое, как указывалось ранее, является следствием уравнений Максвелла. Используем интегральную

Поскольку, согласно граничным условиям (2.70), на поверхности S напряженности полей обращаются в нуль, интеграл в правой части (2.71) также равен нулю. Мы получаем:

Но, согласно начальным условиям (2.69), напряженности полей в начальный момент времени равны нулю, постоянная в правой части (2.72) равна нулю. Это возможно, если только во всем объеме V во все моменты времени

E r, t 0, H r, t 0 , (2.73)

что доказывает теорему.

2.5. Уравнения движения заряженных частиц. Теорема утверждает, в

частности, что единственное решение уравнений Максвелла существует, если

39

известны источники поля – распределение зарядов и токов r, t и j r, t . Поэтому, чтобы полностью определить распределение зарядов и конфигурацию полей в пространстве в произвольный момент времени, уравнения Максвелла следует дополнить уравнениями движения зарядов

В правой части этого уравнения стоит выражение для силы Лоренца (1.81), действующей на заряд со стороны электромагнитного поля.

Так же, как и уравнения электромагнитного поля, уравнения движения заряда могут быть получены из принципа наименьшего действия. При этом необходимо искать вариацию действия не по полевым переменным (потенциалам поля), а по координатам частицы.

Нужно иметь в виду, что электродинамика является релятивисткой теорией, она должна согласовываться с требованиями специальной теорией относительности. На это указывает тот факт, что константа c – скорость света – входит в важнейшие уравнения электродинамики. При скоростях, близких к скорости света, проявляются релятивистские эффекты. Разумеется, когда Максвелл выводил свои уравнения, ни о каких релятивистских эффектах еще не было известно. В 1879 году, в год смерти Максвелла, родился Эйнштейн, который создал специальную теорию относительности в 1905 году. Однако в том и заключается гений великого ученого, чтобы предвидеть дальнейшее развитие теории. Уравнения Максвелла полностью согласуются со специальной теорией относительности, более того, именно развитие электродинамики, в частности, установление экспериментального факта, что скорость света одинакова по отношению ко всем системам отсчета, привело в итоге к созданию специальной теории относительности. Не будем забывать, что работа Эйнштейна 1905 года, в которой формулировалась его теория, носила название "К электродинамике движущихся тел".

40