Electrodynamics

Определение вектора Пойнтинга совпадает с определением (1.76), которое было дано в случае электромагнитных полей в вакууме.

Произведение j,E представляет собой работу электромагнитного поля над сторонними зарядами в единице объема в единицу времени. Кроме того, появляется новый член, характерный для электродинамики сплошных сред, содержащий производные по времени от диэлектрической и магнитной проницаемостей среды:

Появление нового вклада в уравнение баланса неудивительно, так как помимо работы над сторонними зарядами электромагнитное поле совершает работу и над зарядами внутри вещества, вызывая их перераспределение в проводнике или диэлектрике. Совершение этой работы может привести к выделению тепла, связанному с потерями энергии при поляризации и намагничивании. Для того, чтобы получить закон сохранения энергии в окончательном виде, необходимо учитывать термодинамические свойства вещества, в частности, зависимость и от термодинамических параметров (давления, температуры и т. д.).

Закон сохранения энергии (7.59) можно представить в интегральной фор-

7.7. Закон сохранения импульса в сплошной среде. Обратимся теперь к закону сохранения импульса электромагнитного поля. Естественно, что закон сохранения импульса должен выполняться на микроуровне. Умножим третье из

уравнений для микроскопических напряженностей полей (7.1) векторно на h,

101

первое уравнение – векторно на e, второе уравнение умножим скалярно на h, четвертое – скалярно на e. Сложим первое и третье уравнения и вычтем из них второе и четвертое и, после преобразований, повторяющих те, которые были проведены в конце раздела 1, получим закон сохранения импульса:

Здесь π – плотность импульса частиц, Π – плотность импульса электромагнитного поля, которая выражается через микроскопические напряженности полей аналогично (1.92),

ij – тензор плотности потока импульса, следующая формула дает его выра-

жение через напряженности микрополей:

Перейдем к усредненным уравнениям (7.39). Умножим третье уравнение векторно на B, первое уравнение – векторно на D, второе уравнение умножим скалярно на H, четвертое – скалярно на E. Сложим первое и третье уравнения и вычтем из них второе и четвертое:

102

Как и в законе сохранения энергии (7.63), здесь появляются дополнительные члены, феноменологически учитывающие силы, действующие на вещество

вприсутствии электромагнитного поля.

7.8.Принцип взаимности Лоренца. Получим соотношения, являющиеся следствием уравнений Максвелла и известные под названием принцип взаимности или теорема взаимности. Рассмотрим два расположенных в среде источника электромагнитного поля, генерирующие волны одинаковой частоты .

Первое из этих уравнений умножим скалярно на H2 , второе – на E2 , третье – на H1 , четвертое – на E1 . Складывая первые два и вычитая из них третье и четвертое, получим:

H2 ,rot E1 E2 ,rot H1 H1 ,rot E2 E1 ,rot H2

(7.85)

(7.86)

(7.87)

Далее необходимо использовать уравнения связи между E и D, H и B. В принципе, среда может быть достаточно неоднородна и анизотропна. Потребуем лишь, чтобы выполнялись линейные соотношения (7.51), (7.52). Тогда

105

Здесь мы воспользовались тем, что тензор диэлектрической проницаемости среды ij является симметричным. Для доказательства этого факта используют-

ся термодинамические соотношения для диэлектриков. Аналогично,

Таким образом, (7.85) принимает вид:

div E1 ,H2 H1 ,E2 4c E2 , j1 E1 , j2 . (7.90)

Проинтегрируем (7.90) по пространству и преобразуем, как обычно, интеграл по объему от дивергенции в интеграл по бесконечно удаленной поверхности, равный нулю:

Последнее соотношение устанавливает связь между двумя источниками и создаваемыми ими полями в местах расположения источников в одной и той же среде. Фактически, интегрирование в (7.93) происходит по объему источников, т. е. по тем областям пространства, в которых плотность тока отлична от нуля. Если мы предположим, что источниками являются тонкие провода, влиянием каждого из них на поле другого провода можно пренебречь, и поэтому E1 и E2 в (7.93) можно рассматривать как поля излучения первого и второго источников, создаваемые каждым из них в месте нахождения другого источника, как если бы другого источника не было. Формула (7.93) выражает принцип взаимности (иногда также называемый принципом взаимности Лоренца). Он устанавливает соотношение между источниками и создаваемыми ими электриче-

106

скими полями, причем это соотношение не изменится, если мы поменяем местами точки пространства, в которых находятся источники и в которых измеряются напряженности полей.

Если размеры источников малы по сравнению с расстоянием между ними, а также по сравнению с длиной волны излучения, поле каждого источника слабо меняется внутри объема другого источника, и в данном приближении мы можем вынести E1 и E2 из под интегралов в (7.93):

(1) и (2) в (7.94) указывают на то, что напряженности полей берутся в местах расположения первого и второго источников, соответственно. Далее,

Согласно (7.8), интеграл, стоящий под знаком производной по времени в (7.95), представляет собой дипольный момент источника. Поскольку источник создает поле с частотой , то

(это соотношение справедливо для каждого из источников). Тогда из (7.94) получаем принцип взаимности в форме

Втакой форме теорема применима только к дипольному излучению.

7.9.Принцип взаимности Грина. Принцип взаимности существует также в электростатике (так называемый принцип взаимности Грина). Пусть имеются два источника поля с плотностью заряда 1 и 2 . Поля, создаваемые эти-

ми источниками, удовлетворяют уравнениям

Источники находятся в неоднородной анизотропной среде, для которой справедливо соотношение (7.51). Напряженность электрического поля E выразим через градиент скалярного потенциала так же, как она выражается для электростатического поля в вакууме:

Умножим первое из уравнений (7.98) на потенциал 2 , второе – на потенциал1 , вычтем второе из первого и проинтегрируем по объему:

В левой части выделим полную дивергенцию:

2 i ij j 1 1 i ij j 2 dV

Здесь мы вновь воспользовались симметричностью тензора ij . Выбирая по-

верхность S бесконечно удаленной, мы получаем, что левая часть (7.102) равна нулю. Это приводит нас к принципу взаимности Грина:

108

Подобно принципу взаимности Лоренца (7.93), принцип взаимности Грина (7.103) устанавливает связь между двумя зарядами и создаваемыми ими статическими полями в местах расположения зарядов в одной и той же среде.

7.10. Условия на границе раздела двух сред. В заключение этого разде-

ла рассмотрим условия на границе двух сред. Граничные условия легко выводятся из уравнений Максвелла в интегральной форме,

DdS 4 dV.

Пусть имеется граница двух сред с различными диэлектрическими и магнитными проницаемостями. Воспользуемся первым их уравнений Максвелла (7.106). Рассмотрим бесконечно малый замкнутый прямоугольный контур L, лежащий в плоскости, перпендикулярной границе раздела сред (рис. 5).

Рис. 5.

Пусть l1 – длина стороны контура, параллельной границе раздела сред, l2

– длина боковой стороны, перпендикулярной границе раздела. Циркуляция напряженности электрического поля по замкнутому контуру сложится из вкладов сторон, параллельных границе раздела сред, и боковых сторон. Устремляя к ну-

109

где E1 , E2 – тангенциальные составляющие напряженности электрического поля (касательные по отношению к границе раздела сред) в первой и второй средах, соответственно. С другой стороны, интеграл по поверхности S, ограниченной контуром L, в правой части первого уравнения Максвелла также стремится к нулю, поскольку в рассматриваемом пределе стремится к нулю площадь контура.

Из (7.107) следует непрерывность тангенциальных составляющих напряженности электрического поля:

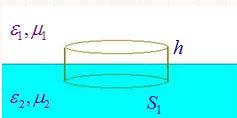
мальных составляющих вектора электрической индукции. Чтобы их получить, рассмотрим бесконечно малый цилиндр, основания которого расположены параллельно границе раздела сред (рис. 6).

Рис. 6.

Пусть S1 – площадь основания цилиндра, S2 – площадь боковой поверхности, h – высота цилиндра. Если мы устремим высоту цилиндра к нулю, h 0 , вклад в поток электрической индукции через поверхность цилиндра будут давать только его основания:

где D1n , D2n – нормальные составляющие вектора электрической индукции по отношению к границе раздела сред в первой и второй средах, соответственно. Интеграл по объему цилиндра от плотности заряда в правой части четвертого

110