Electrodynamics

v – скорость движения заряда. Окончательно,

Потенциалы (4.39), (4.41) называются потенциалами Лиенара – Вихерта.

При вычислении напряженностей электрического и магнитного полей по формулам (2.5), (2.2) мы должны учесть, что в результате интегрирования в (4.37) (после снятия -функции) все величины в (4.39), (4.41) стали формально зависеть от t0 – корня уравнения (4.35), который, в свою очередь, зависит от t, а также от x, y, z, но лишь неявно. В результате вычислений получаются следующие выражения:

71

Часть III. Электромагнитные поля на больших расстояниях

5.Поля статических систем зарядов и токов

5.1.Разложение скалярного потенциала в ряд по малым параметрам.

Рассмотрим поле, создаваемое статической системой зарядов на расстояниях, больших по сравнению с размерами системы. Пусть начало координат находится где-то внутри системы зарядов. Радиус-векторы отдельных зарядов обозначим ra . Тогда скалярный потенциал, создаваемый всеми зарядами в точке с ра-

диус-вектором r, равен

Здесь, как обычно, Ra r ra – радиус-вектор, проведенный из точки, где находится заряд, в точку наблюдения (рис. 3).

получаем с точностью до членов первого порядка:

5.2. Дипольный момент системы зарядов. Дипольным моментом сис-

темы зарядов называется сумма

Если сумма всех зарядов равна нулю. дипольный момент не зависит от выбора начала координат. Действительно, радиус-векторы ra и ra в двух различных системах координат связаны между собой соотношением

мы и их радиус-векторы, соответственно. При этом

73

– радиус векторы центров положительных и отрицательных зарядов (по аналогии с центром масс). Если сумма положительных зарядов равна по модулю сумме отрицательных зарядов,

– радиус вектор от центра отрицательных зарядов к центру положительных зарядов, то

В частности, если система состоит из двух противоположных по знаку зарядов, то R – радиус вектор, направленный от отрицательного заряда к положительному.

5.3. Тензор квадрупольного момента системы зарядов. Рассмотрим следующий член разложения.

74

Dij – тензор квадрупольного момента системы,

Q ea – суммарный заряд системы.

a

Из определения тензора квадрупольного момента следует, что сумма его диагональных компонент равна нулю:

Тензор является симметричным и поэтому имеет только пять независимых компонент. Если полный заряд системы и ее дипольный момент равны нулю, то тензор квадрупольного момента не зависит от выбора начала координат.

Рассматривая последующие члены разложения, можно вычислить высшие мультипольные моменты.

Вычислим напряженность электрического поля:

Напряженность электрического поля статической системы зарядов можно представить следующим образом:

75

–поле квадруполя и т. д.

5.4.Разложение векторного потенциала в ряд по малым параметрам.

Аналогично можно рассмотреть разложение векторного потенциала в случае стационарного магнитного поля. Будем исходить из общего выражения (1.29) для векторного потенциала:

Продолжим преобразование полученного выражения. В первом члене выделим полную производную по времени, второй разобьем на две одинаковые части, в одной из которых также выделим полную производную по времени. При этом необходимо учитывать, что радиус-вектор r, проведенный в точку наблюдения, зависит только от выбранной точки наблюдения, а не от времени, и поэтому

76

должен рассматриваться как постоянный вектор. С другой стороны, магнитное поле создается движущимися зарядами, и, следовательно, радиус-вектор каждо-

Поскольку мы интересуемся стационарным магнитным полем на больших расстояниях от системы зарядов, мы предполагаем, что эти заряды совершают движение в ограниченной области пространства. Такое движение носит стационарный характер, и для получения окончательного выражения для векторного потенциала нужно усреднить по времени выражение (5.34).

Среднее значение производной по времени от всякой величины, изменяющейся в конечном интервале значений, равна нулю. Действительно, если f – такая функция, тогда среднее значение производной за некоторый интервал времени T

Поскольку f ограничена, при увеличении T среднее значение (5.35) стремится к нулю:

В выражение (5.34) входят производные по времени от величин, изменяющихся в конечном интервале значений, которые при усреднении дают нулю. Опуская знак усреднения в дальнейших формулах, получим окончательно:

Мы видим, что в случае стационарного магнитного поля в разложении отсутст-

вует член, пропорциональный 1r , аналогичный кулоновскому потенциалу.

5.5. Магнитный момент системы зарядов. Введем вектор магнитного момента системы

Используя методы векторного анализа, вычислим напряженность магнитного поля:

Проведем дальнейшие преобразования, используя формулу

Выражение для напряженности магнитного поля через магнитный момент в точности совпадает с выражением (5.29) для напряженности электрического поля через дипольный момент.

Если у всех зарядов системы одинаково отношение заряда к массе,

где M ra ,pa – механический момент импульса системы зарядов. В этом

a

случае отношение магнитного момента к механическому постоянно и равно

79

6.Излучение электромагнитных волн

6.1.Разложение запаздывающих потенциалов в ряды по малым па-

раметрам. Вновь рассмотрим поле, создаваемое системой зарядов на больших расстояниях, однако теперь откажемся от требования статичности системы. Начало координат по-прежнему находится где-то внутри системы зарядов, r – ра- диус-вектор точки наблюдения, n – единичный вектор в направлении r. Обозначим через r' радиус-вектор элементарного объема dV с зарядом de dV .

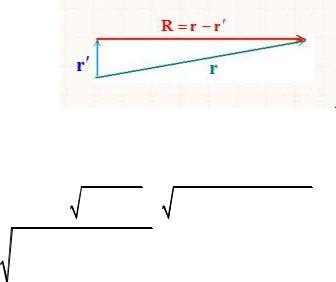
Радиус-вектор, проведенный от элементарного объема dV в точку наблюдения, R r r (рис. 4).

Рис. 4.

На больших расстояниях от системы r r , поэтому

сравнению с r. При интегрировании по dV r является постоянным и может быть вынесен за знак интеграла. В то же время мы должны учесть возможные