2-Гидромеханика 1

52

Глава IV

Динамика идеальной (невязкой) жидкости

В динамике рассматриваются силы, действующие внутри движущейсяжидкости, ито, вкакомсоотношениинаходятсяоник кинематическим характеристикам потока, а также с какой силой действуетпотокнаобтекаемыеимтелаикаковареакцияпоследних нанабегающийпоток.

Сначала рассмотрим динамику некоторой абстрактной жидкости, не имеющей свойства вязкости. Такую абстрактную жидкость, у которой, следовательно, при движении не будут возникать касательные напряжения (не будет трения), назовем

невязкой жидкостью.

Дифференциальные уравнения движения идеальной жидкости (уравнения Эйлера)

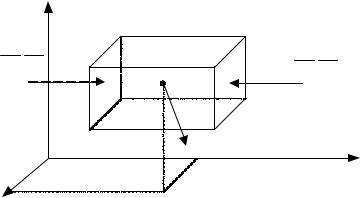
Выделим в массе движущейся жидкости с плотностью ρ элементарныйпараллелепипед(рис. 4.1) сребрамиδ x, δ y иδ z. Масса параллелепипеда ρδ xδ yδ z. Единичные массовые силы Fед с проекциямиFедx, Fедy, Fедz, действующиминаэлементарныйпараллелепипед. Гидродинамическоедавлениевцентрепараллелепипедаp=

= p(x, y, z, t).

Суммапроекцийдействующихмассовыхиповерхностныхсил равнапроизведениюмассыпараллелепипеданапроекциюускорения

53

егоцентра

или

Записав по аналогии два других уравнения, получим диф-

ференциальныеуравнениядвиженияневязкойжидкости(уравнения

Эйлера)

Fедx − ρ1∂∂ px = dudtx , Fедy − ρ1∂∂ py = dudty , Fедz − ρ1∂∂ pz = dudtz .

Впроекцияхнакасательнуюклиниямтока

FедS − ρ1∂∂ Sp = dudt ,

где FедS – проекция ускорения массовых сил на направление касательной, du/dt – касательное ускорение.

Уравнения Эйлера справедливы как для капельных жидкостей, так и для газов.

Для жидкости в покое правые части будут равны нулю. Уравнения Эйлера можно представить в развернутой форме

56

ноль, т. е. когда

или

Это уравнение справедливо лишь для тех случаев, когда определительравеннулю. Выясним, какиеслучаиустановившегося движенияжидкостибудутиметьместо, когдаопределительравен нулю.

Уравнение Бернулли выражает закон постоянства удельной энергии в потоке невязкой жидкости.

Области применимости уравнения Бернулли в установившемся потоке невязкой несжимаемой жидкости

Определитель обращается в нуль, если какой-либо столбец илистрочкаполностьюпредставленынулямииесликакие-либодве строчкипропорциональныдругдругу.Рассмотримследующиеслучаи.

1. ω x = 0, ω y = 0, ω z = 0.

Этоусловиебезвихревого(потенциального) движения. Значит, уравнениеБернуллиприменимоковсемупотенциальномупотокув целом.

Удельный запас энергии движущейся идеальной жидкости одинаков по всему потоку.

2.dx = dy = dz – уравнениелиниитока. ux uy uz

Уравнение Бернулли действительно и при вихревом движении, нотолькодлякаждойотдельнойлиниитока. Удельныйзапас энергии будет постоянным только для каждой линии тока, для различныхлинийтока будетразличным.

значения компонентов вихря из нашего уравнения

уравнениелиниивихряпринимаетвидуравнениялиниитока, т.е. в этомпотокелиниявихрясовпадаетслиниейтока.

Частицы жидкости движутся по линии тока и вращаются вокруг последней. Такое движение называется винтовым. Удельнаяэнергиянезависитоткоординат, таккакеепроизводная по координатам обращается в ноль. Следовательно, в винтовом потоке, так же как и в потенциальном, удельная энергия частиц жидкости одинакова во всем потоке.

УравнениеБернуллиприменимоковсемувинтовомупотокув целом.

Уравнение Бернулли для случая установившегося движения невязкой жидкости, когда из объемных сил на жидкость действует только сила тяжести (случай абсолютного движения)

Дляпотокажидкостисабсолютнымдвижениемкомпоненты объемных сил

Подставивэтизначениявуравнение

60

Геометрическаяинтерпретация ГеометрическийсмыслуравненияБернуллизаключаетсявтом,

чтовсеегочленыимеютлинейнуюразмерность, т. е. онимогутбыть представленыввыбранноммасштабеввидеотрезков, исуммаэтих отрезковвеличинапостоянная.

z – определяет высоту положения над плоскостью сравнения различных точек потока. Может быть ординатой точки на определеннойлиниитока, наопределеннойвихревойлинии, а при винтовом или потенциальном движении – ординатой любойточкипотокаиназываетсягеометрическойвысотой, или

u2

гатьсясвертикальнонаправленнойскоростьюu.Член 2g называ-

етсяскоростнойвысотой, илискоростнымнапором.

УравнениеБернуллипоказывает,чтодлявсехточекданнойлинии токаилиданнойвихревойлинии(адляпотенциальногоивинтового потоковдлявсехточекпотока) сумматрехвысот– геометрической,

пьезометрическойискоростной– естьвеличинапостоянная.

ОбычносуммутрехуказанныхвеличинобозначаютчерезH и

называютполнымгидравлическимнапором

z + ρp + u2 = H . g 2g

Из сказанного следует, что каждый из этих напоров может изменяться, носуммаихостаетсянеизменнойдляслучаядвижения невязкойжидкости. Геометрическоеместоверхнегоконцаполного гидравлическогонапорарасположитсянаопределеннойгоризонтальной плоскости, находящейся над плоскостью сравнения. Эта плоскостьназываетсянапорнойплоскостью.

Геометрическоеместоверхнихконцовсуммыотрезков z + ρ pg

называютпьезометрическойлинией.