
2-Гидромеханика 1
.pdf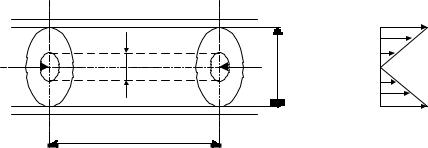
71
Длякаждойтрубысуществуетнекоторыйдиапазонзначений числа Reкр, при котором происходят смены режимов жидкости. На Reкр влияют шероховатость, трубопроводная арматура, возмущения, сужения и т.п.
Переход ламинарного движения к турбулентному удаётся задержатьдосозданиявесьмабольшихзначенийчислаRe (вопытах до100 000), втовремякаквосстановлениеламинарногодвижения при переходе к нему от турбулентного осуществляется при относительномалыхзначенияхчислаRe.
Распределение касательных напряжений в круглой цилиндрической трубе
Рассмотрим равномерное движение жидкости на участке l в прямой горизонтальной трубе с радиусом r0. Так как движение равномерное, товсесилы, действующиенарассматриваемыйотсек жидкости, находятсявравновесии:
p1
( p1 − p2 )πr02 − τ 0 2π r0l= 0. |
|
|
|
|
τ 0 |
2r |
p2 d=2r0=4R |
τ |
l
Рис. 6.2
Преобразуяусловиеравновесия, получим
τ 0 = |
p1 − p2 |
|
r0 |
. |
|
l |
2 |
||||
|
|
||||
Приравномерномдвижении(v1=v2) вгоризонтальнойтрубе(z1= = z2) имеем α 1= α 2= α . Подставив эти значения в выражение для гидравлическогоуклона
|
|
|
|
z |
+ |
p1 |
+ |
α 1v12 |
|
− |
z |
|
+ |
p2 |
+α |
2v22 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||
|
hтр |
|
1 |
|
ρ g |
2g |
|
|
|
ρ g |
|
2g |
|
|
|
||||
I = |
= |
|
|
|
|
|
|
|
|
|
|
, |
|||||||
l |
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
получим

72
I = p1 − p2 , ρ gl
откуда |
p1 − p2 |
|
|
ρ gI= |
. |
||
|
|||
|
l |
||
Подставивданноевыражениевпредыдущуюформулу, получим
|
τ 0 = ρ |
gI |
r0 |
, |
|||
|
|
||||||
или |
|
|
|
|
2 |
|
|
|
τ 0 |
|
|
ρ gI . |
|||
|
|
|
= |
||||
|
|
r |
|||||
|
|
|
2 |
|
|||
|
0 |
|
|
|
|
|
|
Аналогичноизложенномуможносоставитьусловияравновесия дляцилиндражидкостисрадиусомr < r0, выделенноговнутритрубы. Вэтомслучаевуравнениеравновесиявойдетвместокасательного напряжения у стенки трубы τ 0 касательное напряжение между соприкасающимисяповерхностямижидкостиτ , котороебудетравно
τ = ρ gI 2r ,
гдеr/2 – гидравлическийрадиусвыделенногоцилиндра. Изсопоставленияполучаем
τ 0 |
= |
τ |
, |
или τ = τ |
|
r |
. |
r |
r |
|
|||||
|
|
|
0 r |
||||
0 |
|
|
|
|
0 |
|
|
Касательное напряжение по сечению трубы изменяется по линейномузакону, чтосправедливодлялюбогорежимадвижения жидкости. Вопрос о потере напора необходимо рассматривать раздельнодляламинарногоитурбулентногодвижения.
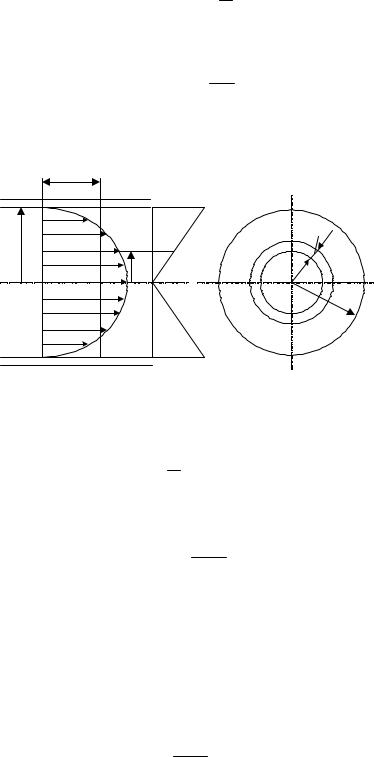
Распределение скоростей u по живому сечению при ламинарном равномерном установившемся движении жидкости
Рассмотримнапорнуюкруглоцилиндрическуютрубу(рис.6.3), имеющую радиус r0. Поставим себе цель найти уравнение эпюры скоростейдляживогосечения.
Для этого внутри данной трубы выделим центральный круглоцилиндрический столб движущейся жидкости (заштрихован) радиусом r. Для продольного касательного напряжения трения τ по боковой поверхности этого столба можно написать два разных выражения:
73
1)согласноуравнениюравномерногодвиженияимеем
τ= ρ gI 2r ,
2)согласнозаконуНьютонаполучаем
τ = −µ dudr ,
здесь при выбранном направлении r (рис. 6.3) величина du/dr отрицательна.
v |
|
τ0 |
|
|
|
|
|
u |
|
|
dr |
r0 |
|
τ |
r |
umax |
r |
|
|
|
|
||
|
|
|
r0 |
Рис. 6.3
Решаясовместноэтиуравнения, получаем
ρ gI 2r = −µ dudr ,
или
du = − ρ2gI rdr.
Интегрируяэтоуравнение, имеем
|
∫u du = − |
ρ gI |
∫ rdr, |
или |
0 |
2µ |
|
|
|
|
u = − ρ4gIµ r2 + C.
ПостояннуюинтегрированияСнаходимизусловия, чтоприr = = r0 величинаи = 0 (какбылоотмеченоранее, непосредственнона стенке русла скорость и должна равняться нулю). Окончательно получаемследующееуравнение, покоторомуможнопостроитьэпюру скоростейдляживогосечения:

74
u = ρ4gIµ (r02 − r2 ),
гдеI – гидравлическийуклон.
Каквидноизуравнения, эпюраскоростейявляетсяпараболой. Подставляя в уравнение r = 0, получаем максимальную величину скоростиumax (вцентретрубы)
umax
Тогдаможнонаписать
|
|
u = |
umax |
(r2 |
− r2 ), |
|
||||||||
|
|
|
|
|
||||||||||
|
|
|
|
r |
2 |
|
|
0 |
|
|
|
|
||
или |
|
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||
|
u |
|
|
|
|
r |
2 |
|
|
|||||
|
= 1 |
− |
|
|
|
|
= 1 |
− |
r |
. |
||||
|
|
|
|
|
|
|
|
|||||||
|
umax |
|
|
|
|
|
r02 |
|
|
|
|
r0 |
|
|
|
2πumax |
r0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r0 |
|
|
|
|
|
2πumax |
r0 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||
Q = |
|
∫(r0 |
− r |
|
) rdr |
= |
2πumax ∫ rdr − |
|
|
∫ r |
dr = |
|||||||||||||||||
r2 |
|
|
r2 |
|||||||||||||||||||||||||
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
0 |
|
|
|
= πu |
|
|
r |
2 |
− |
|
πu |
|
r2 |
= |
πr |
2 |
u |
|
|
. |
|
|
||||||||
|
|
|
|
|
|
|
|
max 0 |
|
0 |
max |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
max 0 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ОтсюдаделениемрасходанаплощадьживогосеченияS = π r 2 |
||||||||||||||||||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
Q |
|
|
|
πr |
2 |
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|||||
|
|
v = |
= |
|
u |
|
|
πr |
2 |
= |
max , |
|
|
|
||||||||||||||
|
|
|
|
|
|
0 |
max |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
S |
|
|
|
|
2 |
|
|
|
|
0 |
|
|
|
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
75
т. е. средняя скорость в ламинарном потоке в круглой трубе равна половине максимальной скорости.
Подставив в данное уравнение значение максимальной скорости, получимследующеевыражениедлясреднейскоростипри ламинарномрежиме:
|
ρ gI |
r |
2 |
|
ρ gr2 |
ρ |
gd 2 |
|
|
v = |
|
0 |
= |
0 |
I = |
|
|
I , |
|
|
|
32 µ |
|||||||
|
4µ 2 |
|
|
8 µ |
|
|
|||
гдеI – гидравлическийуклон
I = ρ32gdv2 .
Потери напора при ламинарном режиме движения жидкости
Потериудельнойэнергии(напора) подлине
hдл. = λ l v2 , d 2g
тогда
hдл = λv2 , l 2gd
гдеhдл/l – гидравлическийуклон.
Приравнявдвауравнениягидравлическогоуклона, получим
32µv |
= |
λv2 |
, |
|
ρ gd 2 |
2gd |
|||
|
|
изнихнайдемзначениекоэффициентаДарси
λ = 64ρvdµ = 64vdν .
Отсюда приходим к заключению, что при ламинарном режиме
λ = Re64 .
Потеринапора(удельнойэнергии) подлине
h |
= |
64 l |
v2 |
. |
|||
|
|
|
|
|
|||
дл |
|
Re d 2g |
|
||||
|
|
|
|||||
Эторавенствопоказывает, чтовслучаеламинарногодвижения потерянапораhдл:
76
1)зависит от свойств жидкости, что учитывается коэффициентомвязкостиν ;
2)прямопропорциональнасреднейскоростиv впервойстепени;
3)независитотшероховатостистенокрусла– вформулуне входяткакие-либохарактеристикишероховатостистенокрусла.
Ламинарноедвижениенаблюдаетсяувязкихжидкостей. При ламинарном режиме стенки русла всегда проявляют себя как гидравлическигладкие.
Многочисленные эксперименты полностью подтверждают правильность полученных теоретических выводов для прямых участков трубопровода, удаленных от входа (l > 0,065d Re), а тем самымиправильностьформулывязкостноготрения, положеннойв основуэтихвыводов.
Коэффициент α при ламинарном режиме движения
Знаязаконраспределенияскоростейпосечениютрубы, легко определить коэффициент Кориолиса α , учитывающий неравномерностьраспределенияскоростейвуравненииБернуллидляслучая стабилизированноголаминарноготеченияжидкостивкруглойтрубе. Дляэтоговвыраженииα ,полученномранее, заменимдействительную скоростьвыражениемдляламинарноготеченияисреднюю скорость выражением,полученнымранее,атакжеучтем,чтоS = πr02 иdS = 2πrdr. Послеподстановокисокращенийполучим
|
|
|
|
|
|
r0 |
|
ρ gI |
|
2 |
− r |
2 |
|
3 |
|
|
1 |
|
u |
3 |
∫ |
4 |
(r0 |
|
) |
2πrdr |
|||||
α = |
dS= |
0 |
|
|
|
|
|
|
|
= 2. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
S |
∫S |
v |
|
|
|
|
2 |
|
ρ gIr2 |
3 |
|
|||
|
|
|
|
|
|
|
|
πr0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
||
Итак,действительнаякинетическаяэнергияламинарногопотока с параболическим распределением скоростей в 2 раза превышает кинетическую энергию того же потока, но при равномерном распределениискоростей.
Изложеннаятеорияламинарноготеченияжидкостивкруглой трубе хорошо подтверждается опытом, и выведенный закон сопротивленияобычноненуждаетсявкаких–либопоправках.

|
|
|
|
|
|
77 |
|
Линии вихрей при ламинарном режиме движения |
|||||||
z |
|
Установившееся ламинарное дви- |
|||||
|
жение является в полном смысле слова |
||||||
|
|
||||||
|
|
установившимсядвижением. Линиитоков |
|||||
0 |
ux |
внемсовпадаютстраекториямичастиц, |
|||||
как это наглядно видно из опытов с |
|||||||
|
x |
||||||
y |
|
окрашиваниемструй. Ноненужнодумать, |
|||||
|
какэтоможетнапервыйвзглядпоказаться, |
||||||
|
|
||||||
|
Рис. 6.4 |
что ламинарное движение является без- |
|||||
|
вихревым. |
|
|
|
|||
|
|
|
|
|
|||
Полескоростейламинарногопотока(научастках, удаленныхот |
|||||||
входа (l > 0,065d Re) относительно системы координат с осью 0x, |
|||||||
совпадающейсосьютрубы, определитсяуравнениями |
|||||||
|
|
uy= 0, |
uz= 0, |
|
|||
асогласноранееполученномууравнению |
|
||||||
|
|
ρ gI 2 |
− (y |
2 |
|
2 |
|
|
ux = |
4µ r0 |
|
+ z |
) , |
||
т. е. полескоростейхарактеризуетсяединственнымкомпонентомпо |
|||||||
оси0x, совершеннонезависящимоткоординатых. |
|||||||
Пополученнымранее формулам(стр. 43, 44) можноустановить |
|||||||
наличиекомпонентовугловойскорости, которыебудутравны |
|||||||
ωx =
ωy =
ωz =
1 |
|
|
∂ uz |
− |
||||
|
|
|||||||
2 |
∂ y |
|||||||
|
|
|
|
|||||
1 |
|
|
∂ u |
x |
− |
|||
|
|
|
|
|||||
2 |
|
|
|
|
||||
|
|
∂ z |
|
|
||||
1 |
|
|
∂ uy |
|
− |
|||
|
|
|
|
|
|
|
||
2 |
|
|
∂ x |
|
||||
|
|
|
|
|||||
∂ |
u |
y |
|
= 0, |
|
|||
|
|
|
|
|||||
∂ |
z |
|
||||||
|
|
|
|
|||||
∂ u |
z |
|
= − |
ρ gI |
z, |
|||
|
|
|
|
|||||
∂ x |
4µ |
|||||||
|
|
|
||||||
∂ ux |
|
= + |
ρ gI |
y. |
||||
|
||||||||
|
4µ |
|||||||
∂ y |
|
|
||||||
Дифференциальноеуравнениевихревойлини
dx = dy = dz |
|
ω x |
ω y ω z |
приметследующийвид:
y dy+dz z=0,

78
илипослеинтегрирования
y2 + z2 = С.
Вихревыелинииявляютсяокружностями, концентрическими относительнооситрубы.Угловаяскоростьвращениячастицжидкости
2 |
2 |
2 |
ρ gI |
2 |
2 |
ρ |
gI |
|
|
ω = ω + ω + ω = |
|
z+ |
y= |
|
|
|
r, |
||
|
|
|
|
||||||
x |
y |
z |
4µ |
|
|
|
4 µ |
|
|
или |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
ω = 2v r,
таккак
r02
ρ gI = 2v .
4µ r02
Следовательно, угловая скорость вращения частиц при ламинарномдвижениипрямопропорциональнасреднейскорости потока и расстоянию соответствующей точки от оси трубы.
На оси угловая скорость вращения равна нулю, а у стенок, наоборот, она достигает своего максимального значения
ω max = |
2v |
, |
|
||
поэтому |
r0 |
|
|
|
|
ω = ω max r , r0
т. е. эпюраугловыхскоростейчастицаналогичнаэпюрекасательных напряжений. Касательныенапряженияпропорциональныугловым скоростям.
79
Глава VII
ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ
Учет потерь напора в потоке
При выводе и анализе уравнения Бернулли в предыдущей главеприменительнокэлементарнойструйкеицеломупотокувязкой жидкости потери напора на преодоление гидравлических сопротивлений, невходявразборфизическойсущностиее, обозначилиhтр.
Дадимподробныйанализэтойвеличиныстем, чтобыполучить формулы для технических расчетов. Общая потеря напора на преодолениегидравлическихсопротивленийсостоитиздвухвидов потерь
1) потери напора по длине потока – hдл,
2) потери на местные сопротивления – hмест.
Если поток состоит из отдельных участков различного сечения и имеет большое количество местных сопротивлений, то общая потеря напора определится как сумма потерь на каждом участкеипотеринавсеместныесопротивления
hтр = ∑ hдл +∑ hмест.
Такой метод подсчета потери напора носит название метода наложения потерь.
Экспериментальноеопределениепотерьнапораосуществляется следующимобразом:
|
|
|
|
p |
|
α 1v12 |
|
|
|
|
|
p |
2 |
|
α |
v |
2 |
|
|
|
h |
= z |
+ |
1 |
+ |
|
|
− |
|
z |
2 |
+ |
|
+ |
|
2 2 |
|
, |
|||
|
|
|
|
|
|
|||||||||||||||
тр |
|
1 |
|
ρ g |
|
2g |
|
|
|
ρ g |
|
|
2g |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где для определения hтр измеряют разность (z1– z2), показания
|
p |
− p |
|
α |
v |
2 |
α |
2 |
v |
2 |
|
|
пьезометров |
1 |
2 |
искоростныхнапоров |
|
1 |
1 |
− |
|
2 |
. |
||
|
ρ g |
|
2g |
|
2g |
|||||||
80
Вгоризонтальной трубе равномерного потока, где v=const,
α=const, z = const, потерянапораопределяетсякак
h = |
p1 |
|
− |
p2 |
|
= |
∆ p |
= ∆ h. |
||
|
|
|
||||||||
тр |
ρ g |
ρ g |
|
ρ g |
||||||
|
|
|||||||||
Обычно потеря напора выражается по ее отношению к |
||||||||||
скоростномунапору |
|
|
|
|
|
|
v2 |
|
|
|
|
h |
|
= ζ |
|
, |
|
||||
|
|
|
|
|
|
|||||
|
|
тр |
|
|
|
2g |
|
|
||
|
|
|
|
|
|
|
|
|
||
где ζ – коэффициент потерь – показывает, сколько скоростных напоровзатраченонапреодолениеданногосопротивления.
Местные потери напора
Местныесопротивления– этовсякогородаизмененияживого сечения или конфигурации потока (когда происходит резкое изменениевеличининаправленийегоскоростей), т. е. расширение или сужение потока, повороты, препятствия в виде диафрагм, кранов, задвижек и т. д.
В зоне местных сопротивлений происходит обтекание местных препятствий с образованием водоворотных зон и интенсивным обменом частицами жидкости основного потока и этих зон. Это и является основным источником местных потерь энергии. Многочисленными опытами установлено, что местные потери подчиняются общему закону потерь энергии, будучи при турбулентном режиме движения пропорциональны квадрату скорости, а в условиях ламинарного режима пропорциональны скоростистепенип <2. Местныепотериэнергиипритурбулентном режимедвиженияопределяютсяпоформуле
h |
|
= ζ |
|
v2 |
, |
|
мест |
мест 2g |
|||||
|
|
|
||||
гдеζмест– безразмерныйкоэффициент, называемыйкоэффициентом местного сопротивления и определяемый опытным путем для каждоговидасопротивлений.
Однако при наличии местных сопротивлений может оказаться, чтоскоростипотокапередместнымсопротивлением и посленегобудутразличны. Втакихслучаях(например, внезапное расширение) местная потеря напора может быть выражена или
