
2-Гидромеханика 1
.pdf41
Глава III
КИНЕМАТИКА ЖИДКОСТИ
Разделгидромеханики, рассматривающий формыдвижений жидкости, не касаясь вопроса о силах, под влиянием которых происходят эти движения, называется кинематикой жидкости.
Способы описания движения жидкости
Под жидкостью в данном случае понимается система материальных частиц (точек), образующих непрерывную, сплошную массу, плотность и формы которой могут изменяться каждое мгновение.
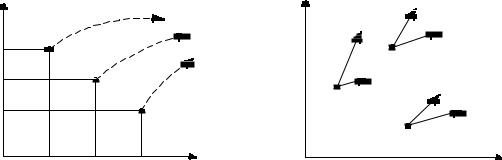
1-й способ (способ Лагранжа). В этом способе задают уравнениямитраекториюкаждойдвижущейсячастицыжидкости.
Дано начальное положение – координаты a, b, c. В каждый последующий момент времени t положение её определяется координатами
где a, b, c и t являются аргументами, определяющими значения различных функций, характеризующих движение некоторой фиксированной частички потока, и называются переменными Лагранжа.
Всилуданноговышеопределенияжидкостибудемполагать, что эти функции непрерывны, т. е. что масса жидкости не распадается во время движения на отдельные части.
Уравнениямогутбытьоднозначноразрешеныотносительноa, b, c. Врезультатеэтогоa, b, c будутопределеныкакфункцииотх, у, z, которые дадут ответ на вопрос о том, в каком месте находилась в начальныймоменттаилиинаячастицажидкостискоординатамих, у, z вданныймоментвремени. Призаданиидвижениявпеременных
42
Лагранжапроекциискоростичастицыu, напримерux, определяютпо формуле
ux = dxdt ,
проекцииускорения– поформуле
ax = |
d 2 x |
. |
||
dt |
2 |
|||
|
|
|||
По этому уравнению можно знать как «историю» движения жидкости, т. е., знаяположениеточки(x, y, z) вданныймомент, мы можемопределить(a, b, c), такиеё«будущее», т.е. влюбоевремяt.
|
|
|
|
|
z |
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
2 |
|
|
|
||
z |
|
Траектория |
|
|
|
|
|
|
( |
|
|
|
|
|
||
M3 |
|
|
|
|
|
|
u |
2 |
|
|
|
|
|
|||
|
|
|
|
|
) |
|
|
|
|
|
|
) |
|
|||
z |
|
|
|
|
|
t |
2 |
|
|
|
|
|
t |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3 |
|
|
|
|
( |
|
|
|
2 |
|
|
( 1 |
|
|||
|
|
M2 |
|
|
u |
1 |
|
|
|
|
|
u2 |
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
|
|
t |
) |
|
|
) |
|
|||
|
|
|
|
|
|
|
|
|
|
t2 |
|
|||||
|
|
|
M1 |
|
|
|
u ( 1 |
|
|
( |
|
|
|
|||
z1 |
|
|
|
|
|
|
1 |
|
|
|
|
u3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
(t ) |
|||
|
|
|
|
|
|
|
|
|
|
|
u |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
0 |
x3 |
x2 |
x1 |
x |
0 |
|
|
|
|
|
|
|
|
|
|
x |
Рис. 3.1. КспособуЛагранжа |
Рис. 3.2. КспособуЭйлера |
|||||||||||||||
2-йспособ(способЭйлера). Вразличныхточкахнеподвижного пространствазадаютсяуравнениемизмененияскоростивразличные моментывремени.
Это пространство характеризуется «полем скоростей», непрерывноменяющимсявовремени. Датьзаконизмененияэтогополя значитвыразитьскоростьu, аследовательно, иеепроекциинаоси координаткакфункциючетырехаргументов– времениt икоординат х, уиz точекнеподвижногопространства:
u=u(x, y, z, t),
ux =ux (x , y, z, t ), uy =uy (x , y, z, t ), uz =uz(x , y, z, t ), ρ =ρ ( x, y, z, t),
где x, y, z, t – переменные Эйлера.
По этим уравнениям можно определить а) скоростьвлюбыхточкахпространствавлюбоевремя;
43
б) скоростьвданнойточкевлюбоймоментвремени(тогдаx = = const, y = const, z = const);
в) скоростьвданныймоментвремени, новразличныхточках пространства(тогдаt = const).
Второй способ, однако, не может разрешить вопроса о поведении частицы в пространстве.
СвязьмеждууравнениямиЛагранжаиЭйлера:
dx |
= u |
x |
(x, y, z,t ) |
, |
dy |
= u |
y |
(x, y, z,t) |
dz |
= u |
z |
(x, y, z,t) |
. |
|
|
|
|||||||||||
dt |
|
dt |
, |
dt |
|
||||||||
|
|
|
|
|
|
|
|
||||||
Интегрируяэтиуравнения, получимx, y, z вфункцииотt итри произвольныепостоянныеa, b, c.
Если в каждой точке неподвижного пространства, занятого движущейсяжидкостью, скоростистечениемвремениизменяются, то движение жидкости называется неустановившимся (уравнения Эйлера). Если скорости не зависят от времени, то движение называетсяустановившимсяиуравненияпринимаютвид
ux=u(x, y, z); uy=u(x, y, z);
uz=u(x, y, z); ρ =ρ (x , y, z) .
Примеромнеустановившегосядвиженияможетслужитьслучай истеченияжидкостиизрезервуарачерезотверстияприпеременном уровне жидкости в нем. В случае истечения жидкости из того же резервуараприпостоянномуровнедвижениебудетустановившимся.
Понятие о вихревом и потенциальном движении жидкости
Учение о движении жидкости основывается на понятии о движении бесконечно малой частицы. Движение твердого тела состоит из поступательного движения u0 и вращательного движения uвр вокруг мгновенной оси, проходящей через полюс, с угловойскоростьюω .
Значения компонентов угловой скорости
ω x |
= |
1 |
|
∂ u |
z |
− |
∂ uy |
; |
||
|
|
|
|
|
|
|||||
2 |
|
|
∂ |
|
||||||
|
|
|
∂ y |
z |
|
|||||

44 |
|
|
|
|
|
|
|
|
|
|
|
ω y |
= |
1 |
|
∂ u |
x |
− |
∂ u |
|
; |
||
|
|
|
|
z |
|
||||||
2 |
∂ z |
|
|
||||||||
|
|
|
|
|
∂ x |
|
|||||
ω z |
= |
1 |
|
∂ uy |
− |
|
∂ u |
|
, |
||
|
|
|
|
|
|
x |
|
||||
2 |
∂ x |
|
|
|
|||||||
|
|
|
|
|
∂ y |
|
|||||
а величина угловой скорости
ω = ω 2+ ω |
2+ ω |
2 . |
x |
y |
z |
При движении жидкой частицы к этим двум движениям добавляется движение, обусловленное деформацией частицы. Следовательно,
Движение, прикоторомпроисходитвращениечастицжидкости,
называетсявихревымдвижением.
Движение, прикоторомотсутствуетвращениечастиц(ω = 0),
называют безвихревым движением.
Еслиω = 0, то
ω x = ω y = ω z =0
иследовательно
∂ u |
z |
= |
|
∂ uy |
; |
|
||
|
|
∂ z |
|
|||||
∂ y |
|
|
|
|
||||
∂ ux |
= |
|
∂ uz |
|
; |
(3.1) |
||
∂ z |
∂ x |
|||||||
|
|
|
|
|||||
∂ ux |
= |
|
∂ uz . |
|
||||
∂ z |
|
|
∂ x |
|
|
|||
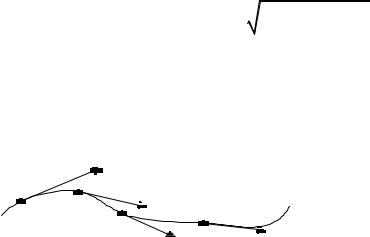
Безвихревоедвижениеназываютпотенциальным, таккакдля выражения проекций скорости ux, uy, uz можно подобрать функциюΦ, называемуюпотенциаломскорости, частныепроизводные которой
∂ Φ |
= −ux , |
∂ Φ |
= −uy , |
∂ Φ |
= −uz , |
||
∂ y |
|
||||||
∂ x |
|
|
∂ z |
|
|||
гдеΦ = Φ(x, y, z, t) – потенциалскорости.
Равенство (3.1) является необходимым и достаточным условием для существования такой функции.
45
Пример
Проверим, к какому виду относится движение, заданное в переменныхЭйлера
ux=–3x, uy=3y, uz=0.
Определимкомпонентыугловойскорости:
ω x = |
1 |
|
∂ u |
z |
− |
∂ uy |
= |
1 |
(0− 0)= 0; |
|||||||
|
|
|
|
|
|
|
|
|||||||||
2 |
∂ y |
∂ |
|
|
2 |
|||||||||||
|
|
|
|
|
|
z |
|
|
||||||||
ω y = |
1 |
|
∂ u |
x |
− |
∂ u |
|
= |
1 |
(0− 0)= 0; |
||||||
|
|
|
|
|
z |
|
|
|||||||||
2 |
|
|
|
∂ |
|
|
2 |
|||||||||
|
|
|
|
∂ z |
|
|
x |
|
|
|||||||
ω z |
= |
|
1 |
|
∂ uy |
|
− |
∂ u |
|
= |
1 |
(0− 0)= 0, |
||||
|
|
|
|
|
|
|
|
|
x |
|
|
|||||
|
2 |
|
∂ x |
|
∂ |
|
|
2 |
||||||||
|
|
|
|
|
|
y |
|
|
||||||||
тогдавеличинаугловойскорости
ω = ω + ω |
+ ω |
= 0, |
2 |
2 |
2 |
x |
y |
z |
т. е. данноедвижениепотенциальное.
Линии токов жидкости и вихревые линии
Траектория – кривая, по которой перемещается частица
u1 |
|
|
жидкости. Линия тока пред- |
u2 |
|
ставляетсобойкривую, вкаждой |
|
|
|
точке которой в данный момент |
|
|
|
u4 |
|
|
u3 |
времени вектор скорости жид- |
|
|
|
Рис. 3.3 |
кости касателен к кривой. При |
|
установившемся движении жид- |
||
|
кости линия тока и траектории движения частиц жидкости, на ней расположенных, совпадают.
Внеустановившемсядвижениилиниитокаитраекториичастиц несовпадают. Каждаячастичканаходитсяналиниитокалишьодно мгновение. Линиятокасуществуеттакжеодномгновенье.
Дифференциальнымуравнениемлинийтоканазываетсяуравнение, полученноеизусловия, чтокасательныеклиниитокасовпадаютс векторомскорости.Направляющиекосинусыугловкасательнойклинии токаравнысоответственно
dxdl , dydl , dzdl ,
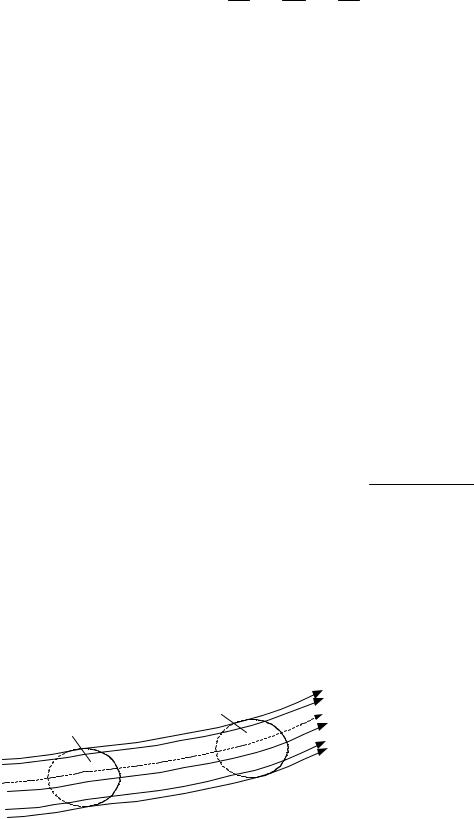
46
где dl – элемент дуги на линии тока, dx, dy и dz – проекции этого элементанаосикоординат. Направляющиекосинусыугловвектора скоростислиниямитокасоответственноравны
uux , uuy , uuz .
Из определения понятия линии тока косинусы углов равны
dx |
= |
u |
x |
, |
dy |
= |
u y |
, |
dz |
= |
u |
z |
, |
dl |
|
|
dl |
u |
dl |
|
|
||||||
|
u |
|
|
|
u |
||||||||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = dy = dz = dl . |
|
|
|
|
|||||
|
|
|
|
ux |
uy |
uz |
u |
|
|
|
|
||
Дифференциальныеуравнениялинийтоковвданныймомент времени
dx |
= |
dy |
= |
dz |
|
|
|
|
, |
||
ux (x, y, z,t ) |
uy (x, y, z,t ) |
uz (x, y, z,t ) |
|||
где t являетсяпараметром.
Аналогично можно получить уравнения вихревых линий (линии, в каждой точке которых вектор угловой скорости совпадаетснаправлениемкасательнойкним)
dx |
|
|
dy |
dz |
||
|
= |
|
|
|
=ω z (x, y, z,t ) |
. |
ω x (x, y, z,t ) |
ω y (x, y, z,t ) |
|
||||
Элементарная струйка жидкости
Поверхность, образуемаялиниямитока, проходящимичерез точки некоторого достаточно малого замкнутого контура,
называется трубкой тока.
|
Жидкость, наполня- |
dS2 |
ющая трубку тока, называ- |
ется элементарной струй- |
|
dS1 |
кой. Обратим внимание на |
|
|
|
разницу в положении эле- |
|
ментарных струек жид- |
|
кости при установившемся |
Рис. 3.4 |
и неустановившемся дви- |
47
жении. В установившемся потоке жидкости струйки будут всегда заниматьустойчивоевовремениположениевпространстве.Наоборот, принеустановившемсядвиженииструйкибудутнепрерывноменять своеположение.
СечениеструйкиповерхностьюdS, нормальнойклиниямтока,
называетсяживымсечением.
Объемное количество жидкости, протекающее в единицу времени через какое-либо живое сечение струйки, называется расходомэлементарнойструйкиδ Q. Отношение
δQ = v
δS
называетсясреднейскоростьювданномпоперечномсеченииструйки. Дляэлементарнойструйки, имеющейбесконечномалыеплощади сечений, можно считать истинную скорость u одинаковой во всех точках каждого сечения. Из данного отношения найдем формулу расходаэлементарнойструйки
δ Q = δ S u.
Уравнение неразрывности жидкости
Условие неразрывности налагает определенные зависи-
мости в общем случае между плотностью и скоростью движу- |
||||||
|
|
|
|
|
|
щихся частиц жидкости, вы- |
z |
|
|
∂u |
|
|
ражающиеся в форме диф- |
+ |
|
ференциального уравнения |
||||
uxdt |
ux |
|
x δx dt |
|||
δx |
|
|
∂x |
|
неразрывности. Для капель- |
|
δy |
|
|
|
|
|
|
|
|
|
|
|
ной жидкости в уравнение |
|
|
|
|
|
|
|
|
δz |
|
|
|
|
|
неразрывности войдут толь- |
|
|
|
|
|
|
коскорости. |
0 |
|
|
|
|
|
Для вывода этого урав- |
y |
|
|
|
|
x |
нения рассмотрим внутри |
|
|
|
|
|
пространства, занимаемого |
|
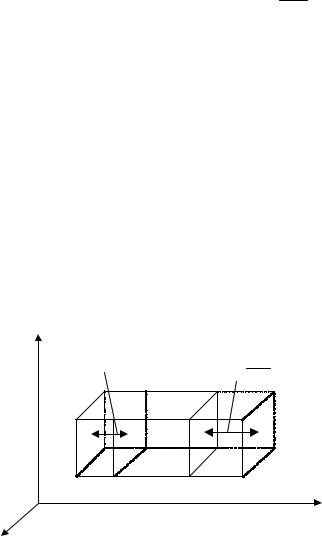
Рис. 3.5 |
|
|
|
|
|
|
потоком, элементарный неподвижный прямоугольный параллелепипед с ребрами δ x, δ y и δ z, через который протекает (втекает и вытекает) жидкость (рис. 3.5). Условие неразрывности требует, чтобы рассматриваемый объем всегда был заполнен полностью протекающей жидкостью.

48
Масса поступающего объема жидкости через грань δ z δ y, ближайшуюкплоскостиy0z,
ρ ux δ y δ z dt.
Масса вытекшего объема жидкости через грань δ z δ y, параллельную первой,
|
∂ (ρ u |
) |
|
ρ ux δ y δ z dt+ |
∂ x |
x δ |
δxδ y zdt . |
Черезграниδ z δ x иδ y δ x соответственновходятмассы |
|||
ρ uy δ z δ x dt и ρ uz δ y δ x dt |
|||
и выходят через противоположные грани, параллельные этим площадкам,
|
|
|
|
|
|
|
|
∂ |
(ρ |
uy ) |
|
|
|
|||
|
ρ |
uy δ z δ |
x |
dt+ |
|
∂ |
y |
δ |
δyδ z xdt , |
|||||||
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|||
|
|
|
|
|
|
|
|
∂ |
(ρ |
u |
|
|
|
|
||
|
ρ |
uz δ y δ |
x |
dt+ |
|
∂ |
x |
z δ |
|
δzδ y |
xdt . |
|||||
Изменениемассы, вытекшейизпараллелепипеда, |
||||||||||||||||
|
∂ (ρ u |
x |
) |
|
∂ (ρ uy ) ∂ ρ ( |
u |
z |
) |
|
|||||||
− |
|
|
|
+ |
|
|
+ |
|
|
|
|
δ xδ |
δy zdt, |
|||
|
∂ x |
|
|
∂ |
y |
∂ |
|
z |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
номассажидкостивмоментвремениt быларавнаρ δ x δ y δ z, ачерез dt, еслинепроизошлоразрыважидкости,
ρ δ x δ yδ +z |
∂ δρ |
δ xδ y zdt. |
|
∂ t |
|
Изменение(уменьшение) массызавремяdt
∂∂ ρt δ xδ δy zdt.
Приравнивая эти две величины, получим условие неразрывностижидкости
|
|
|
|
|
|
∂ρ |
|
∂ (ρ |
u |
x |
) |
|
∂ (ρ uy ) ∂ ρ |
( |
u |
z |
) |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
+ |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
= 0, |
|
|
|
||||||
|
|
|
|
|
|
∂ t |
∂ |
x |
|
|
|
∂ |
y |
|
∂ |
|
z |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ uy |
|
|
|
|
|
||||
∂ρ |
|
∂ρ |
|
|
|
|
∂ρ |
|
|
∂ρ |
|
|
|
|
|
|
|
|
∂ u |
x |
|
|
|
∂ u |
z |
|
|
||||||||||
|
|
+ |
|
|
|
|
ux |
+ |
|
|
|
uy |
+ |
|
|
uz |
+ |
ρ |
|
|
|
+ |
|
|
|
|
|
|
+ |
|
|
= 0. |
|||||
∂ |
t |
∂ |
x |
|
|
|
z |
|
|
|
|
|
|
|
|
y ∂ |
|
|
|||||||||||||||||||
|
|
|
∂ y |
|
∂ |
|
|
|
∂ |
|
|
x ∂ |
|
|
|
|
z |
|
|||||||||||||||||||
49
Дифференциальноеуравнениенеразрывностижидкостивформе Эйлера
|
dρ |
|
|
∂ u |
x |
|
∂ uy |
|
|
|
|
∂ u |
|
|
|
|
||||||||
|
|
+ ρ |
|
|
+ |
|
|
|
|
|
+ |
|
|
|
z |
|
= 0. |
|
|
|||||
|
dt |
|
∂ x |
∂ |
y |
∂ |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
z |
|
|
|
||||||||||||||
Длянесжимаемойжидкостиρ |
=const, тогда |
dρ |
= 0, ауравнение |
|||||||||||||||||||||
dt |
||||||||||||||||||||||||
будетиметьвид |
|
∂ u |
|
|
|
∂ uy |
|
|
|
|
∂ u |
|
|
|
|
|
|
|
|
|||||
|
|
|
x |
+ |
|
+ |
|
z |
= 0. |
|
|
|
||||||||||||
|
|
|
|
|
∂ |
y |
|
∂ |
|
|
|
|
|
|||||||||||
|
|
|
∂ x |
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|||||||
Таккакжидкостьнесжимаема, тоэтоуравнениеговоритотом, чтообъемжидкости, втекающейвпараллелепипед, равенобъему, вытекающемуизнего.
Пример
Движениежидкостиприусловииρ = const заданоуравнениями
|
ux= –3x, |
|
uy= 3y, |
|
uz= 0, |
|||||
тогда |
|
|
|
|
|
|
|
|
|
|
|
∂ u |
x |
= −3, |
∂ uy |
= 3, |
|
∂ u |
z |
= 0. |
|
|
∂ x |
∂ |
y |
∂ z |
||||||
|
|
|
|
|||||||
Подставляянайденныезначениявуравнениенеразрывности, получаем
∂ u |
x |
+ |
∂ uy |
+ |
|
∂ u |
z |
= −3 + 3 + 0 = 0. |
|
|
|
∂ |
y |
∂ z |
|||||
∂ x |
|
|
|||||||
Еслибыдвижениебылозадановвиде
ux = –3x, uy = –3y, uz = 0,
тоуравнениенеразрывностинесоблюдалосьбы, чтосвидетельствует онарушениисплошностипотока.
Поток жидкости
Поток жидкости – совокупность элементарных струек жидкости, движущихсясразличнымискоростями.
Потокжидкости– движениемассыжидкости, ограниченной системойповерхностейтвердыхигазообразныхтел.
Вкачествеобщегопримераможноуказатьнапотоквреке. Здесь потокограниченчастичнонеподвижнойповерхностьюложа,частично
– воздухом на свободной поверхности. Поток жидкости в трубе,
50
работающейполнымсечением, являетсяпримеромпотока, ограниченноголишьповерхностьютвердоготела– стенкамитрубы. Струя, вытекающаяизбрандспойтаилиотверстиявсосуде, представляет собой пример потока, ограниченного лишь окружающей средой, напримервоздухом.
Соответственно перечисленным случаям потоки делятся на
1)безнапорныепотоки, т. е. потоки, ограниченныетвердыми стенками, ноимеющимисвободнуюповерхность, например поток в канале;
2)напорные потоки, т. е. потоки, не имеющие свободной поверхности, например поток в водопроводной трубе;
3)гидравлические струи, т. е. потоки, ограниченные лишь жидкостной или газовой средой.
Живое сечение потока – поверхность, проведенная в потоке перпендикулярно линиям тока.
Площадь живого сечения потока
S = ∫ dS ,
S
гдеdS – площадьэлементарнойструйки.
Объемжидкости, проходящейвединицувременичерезживое сечениепотока, называетсярасходомпотокаиравенсуммерасходов элементарныхструек
Q = ∫dQ = ∫u dS.
S S
РазделиврасходQ наплощадьживогосеченияS, получим
Q/S = v.
Вообщескоростидвиженияжидкостивразличныхточкахсечения будутразличными,ипотомусреднююскоростьдлявсегосечениянужно пониматькакнекотороеабстрактноепредставление.
Средняяскоростьвсечениипредставляетсобойодинаковую для всех точек сечения скорость, при которой через сечение проходит такой расход, какой фактически имеет место при действительных скоростях.
Уравнение неразрывности для потока с установившимся движением
Q = v1S1 = v2 S2 = … = vi Si = const.
