
- •Основы измерений и обработки результатов
- •1. Однократные измерения размера линейкой.
- •Ускорение свободного падения
- •Основные теоретические положения
- •Экспериментальная установка и методика измерений.
- •Обработка результатов эксперимента
- •Баллистический маятник
- •Математический маятник
- •Упругий удар Цель работы: исследование удара, изучение законов сохранения импульса и механической энергии при ударе.
- •Коэффициент поверхностного натяжения
- •Измерение газовой постоянной
- •Теплоемкость жидкости
- •Колебания струны
- •Основные теоретические положения
- •Экспериментальная установка и методика измерений
- •Вязкость жидкости
Измерение газовой постоянной
Цель работы:изучение газовых законов, экспериментальная проверка уравнения состояния идеального газа, ознакомление с работой газового термометра.
Основные теоретические положения
В молекулярно-кинетической теории объектом исследования является идеализированная модель реального газа − идеальный газ. Идеальным газом называется газ, между молекулами которого отсутствуют силы взаимодействия. При этом принимается, что при соударениях между собой и со стенками сосуда молекулы такого газа ведут себя как абсолютно упругие шарики конечных, но весьма малых размеров. Эти соударения молекул происходят по законам абсолютно упругого удара.
Величинами,
определяющими состояние газа, являются:
давление р,
под которым он находится, его температура
Т
, объем V,
занимаемый определенной массой газа
М.
Величины p,
V,
T,
M
называются
параметрами состояния. Давлением
Р
называется
физическая величина, равная пределу
отношения
численного значения нормальной силы
![]() ,
действующей
на единицу поверхности
,
действующей
на единицу поверхности
![]() ,
к величине этой поверхности:
,
к величине этой поверхности:
![]()
Единицей
давления
в системе СИ является паскаль
([P]=[F]/[S]=
H/![]() =Па)
=Па)
Температурой называется физическая величина, характеризующая степень нагретости тела.
Параметры состояния связаны между собой различными газовыми законами.
Если газ находится при постоянной температуре T=const, то объем газа и давление связаны законом Бойля-Мариотта pV=const.
При
постоянном объеме
![]() −
это закон Шарля, в котором
−
это закон Шарля, в котором![]() −
термический коэффициент давления,
−
термический коэффициент давления,![]() и
и![]() −
давление газа при начальной и конечной
температуре.
−
давление газа при начальной и конечной
температуре.
П
Рис. 7.1. К выводу
уравнения состояния идеального газа
![]() ,
где
,
где![]() термический
коэффициент объемного расширения,
термический
коэффициент объемного расширения,![]()
![]() −
объемы газа при начальной и конечной
температуре.
−
объемы газа при начальной и конечной
температуре.
Теперь
возвращаемся к уравнению состояния
идеального газа, то есть найдём связь
между P,
V
и
T.
Рассмотрим определённую массу газа m,
которая заполняет объём
![]() ,
имеет давление
,
имеет давление![]() и находится при температуре
и находится при температуре![]() .
Пусть в другом состоянии та же масса
газа характеризуется объёмом, давлением
и температурой:
.
Пусть в другом состоянии та же масса
газа характеризуется объёмом, давлением
и температурой:![]() ,
,![]() ,
,![]() .
Установим на основании законов
Бойля-Мариотта, Гей-Люссака и Шарля
связь между
.
Установим на основании законов
Бойля-Мариотта, Гей-Люссака и Шарля
связь между![]() ,
,![]() ,
,![]() и
и![]() ,
,![]() ,
,![]() .
Для этого сначала газ из состояния
.
Для этого сначала газ из состояния![]() ,
,![]() и
и![]() при постоянном давлении
при постоянном давлении![]() нагреем до температуры
нагреем до температуры![]() .
По закону Гей-Люссака
.
По закону Гей-Люссака![]() .
Так как
.
Так как![]() ,
то
,
то![]() .
Из этого состояния в окончательное
состояние, характеризующееся параметрами
.
Из этого состояния в окончательное
состояние, характеризующееся параметрами![]() ,
,![]() ,
,![]() ,
его можно перевести изотермическим
изменением объёма, для которого по
закону Бойля-Мариотта имеем:
,
его можно перевести изотермическим
изменением объёма, для которого по
закону Бойля-Мариотта имеем:![]() .
Подставляя
.
Подставляя![]() ,
получим
,
получим![]() ,
то есть
,
то есть![]() ,
откуда следует, что при изменении
состояния данной массы газа величинаPV/T
остаётся постоянной, то есть PV/T=B.
,
откуда следует, что при изменении
состояния данной массы газа величинаPV/T
остаётся постоянной, то есть PV/T=B.
Если это соотношение относить к одному молю, то постоянная В будет иметь одно и то же значение для всех газов. Эта общая для всех газов постоянная обозначается R и носит название универсальной газовой постоянной. Вводя в предыдущую формулу вместо объема V молярный объем Vо, то есть объем одного моля газа, получим
![]() .
(7.1)
.
(7.1)
Эта формула представляет собой уравнение состояния идеального газа и носит название уравнения Менделеева-Клапейрона.
Уравнение
Менделеева-Клапейрона, справедливое
для одного моля газа, можно
обобщить и на любую массу. Если
![]() — молярная
масса и при некотором данном
давлении и температуре 1 моль
газа
занимает объем
— молярная
масса и при некотором данном
давлении и температуре 1 моль
газа
занимает объем
![]() ,
то
при том жедавлении
и температуре т
граммов
газа займут объем
,
то
при том жедавлении
и температуре т
граммов
газа займут объем
![]() .
Тогда
.
Тогда![]() и, подставляя в уравнениеМенделеева-Клапейрона
(7.1), получим
и, подставляя в уравнениеМенделеева-Клапейрона
(7.1), получим
![]() .
(7.2)
.
(7.2)
В работе предлагается на опыте убедиться в справедливости формулы (7.2), а также определить универсальную газовую постоянную.
Описание лабораторной установки и последовательность проведения измерений
Рис.
7.2.Экспериментальная установка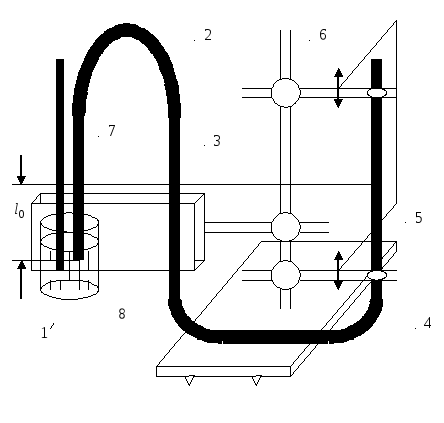
Задание 1. Проверка уравнения состояния идеального газа (7.2).
При
равенстве уровней воды в трубках 3 и 5
измеряется длина воздушного столба
![]() от уровня воды в трубке 1. Объём воздуха
пропорционален длине столба
от уровня воды в трубке 1. Объём воздуха
пропорционален длине столба![]() плюс объём колбы
плюс объём колбы![]() ,
то есть
,
то есть![]() .
Давление воздуха равно атмосферному
.
Давление воздуха равно атмосферному![]() .
Температура воздуха
.
Температура воздуха![]() равна температуре воздуха в лаборатории
и определяется по термометру. Параметры
указанного состояния
равна температуре воздуха в лаборатории
и определяется по термометру. Параметры
указанного состояния![]() ,
,![]() ,
,![]() ,
а величина
,
а величина![]() .
.
Включается
нагреватель, и температура воды в стакане
увеличивается до
![]() .
При
этом уровень воды в трубке 5 поднимается,
то есть газ в колбе 1 расширяется
и его часть
.
При
этом уровень воды в трубке 5 поднимается,
то есть газ в колбе 1 расширяется
и его часть
![]() выходит из объёма колбы. Если перемещать
трубку 5вверх
− вниз на величину
выходит из объёма колбы. Если перемещать
трубку 5вверх
− вниз на величину
![]() ,
то можно добиться равенства уровня воды
в трубках
3 и 5. Тогда давление воздуха в колбе 1
будет равно атмосферному давлению
,
то можно добиться равенства уровня воды
в трубках
3 и 5. Тогда давление воздуха в колбе 1
будет равно атмосферному давлению
![]() ,
а длина воздушного столба или объём
,
а длина воздушного столба или объём
![]() ,
где
,
где
![]() ,
,![]() − поперечное сечение трубки. Получаются
вторые данные
− поперечное сечение трубки. Получаются
вторые данные
![]() ,
,
![]() ,
,
![]() .
Далее
вода
в стакане нагревается до температуры
.
Далее
вода
в стакане нагревается до температуры
![]() и
проделывается то же, что и схолодной
водой. Получается третий набор данных:
и
проделывается то же, что и схолодной
водой. Получается третий набор данных:
![]() ,
,
![]() ,
,
![]() .
Все
полученные данные измерений заносятся
в таблицу.
.
Все
полученные данные измерений заносятся
в таблицу.
Величина
![]() (j=1,2)
рассчитывается следующим образом. В
каждом эксперименте при нагревании
колбы до температуры
(j=1,2)
рассчитывается следующим образом. В
каждом эксперименте при нагревании
колбы до температуры
![]() объём газа в ней увеличивается на
объём газа в ней увеличивается на![]() ,
и при этом высота жидкости в манометре
изменяется на
,
и при этом высота жидкости в манометре
изменяется на
![]() .
Поэтому на основании уравнения (7.2)
.
Поэтому на основании уравнения (7.2)
![]() ,
,
откуда
изменение объёма равно
![]() ,
то есть
,
то есть![]() ,
а
,
а![]() .
.
Обработка результатов и расчёт погрешностей
Приборную погрешность величины
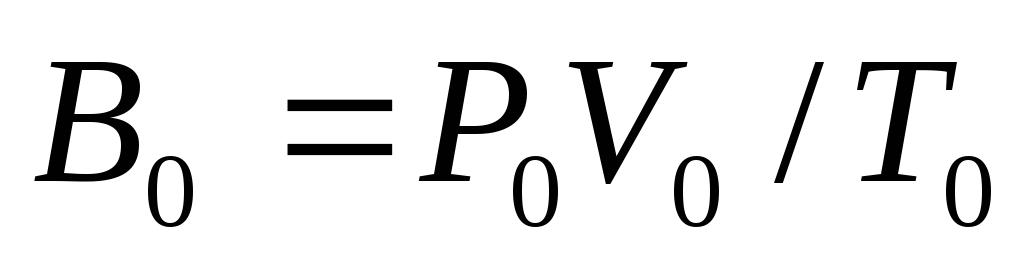 определить по формуле
определить по формуле
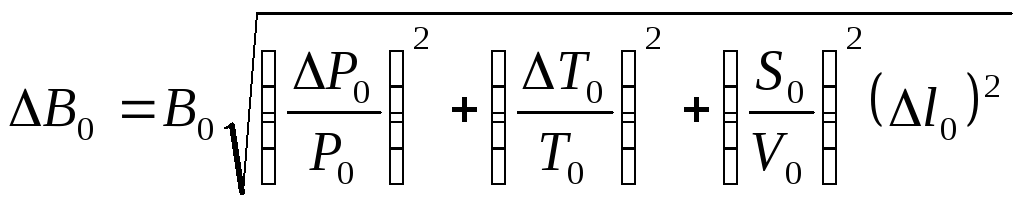 .
(7.3)
.
(7.3)
Результат представить в виде
 .
.Погрешность величины
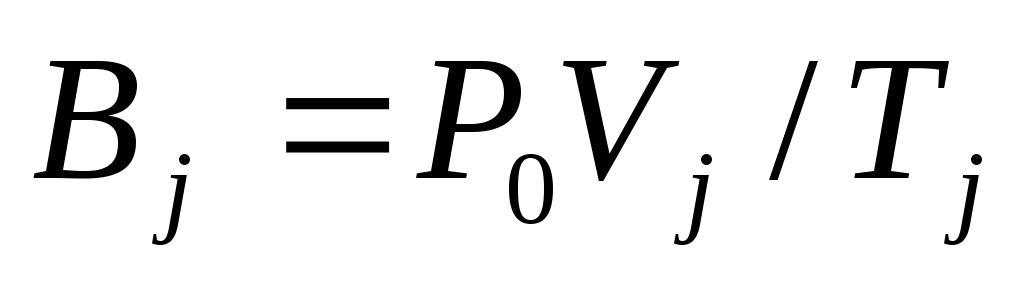 (j=1,2)
рассчитать
по формуле
(j=1,2)
рассчитать
по формуле
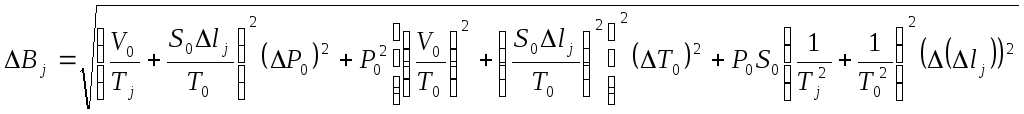 . (7.4)
. (7.4)
Результат представить в виде:
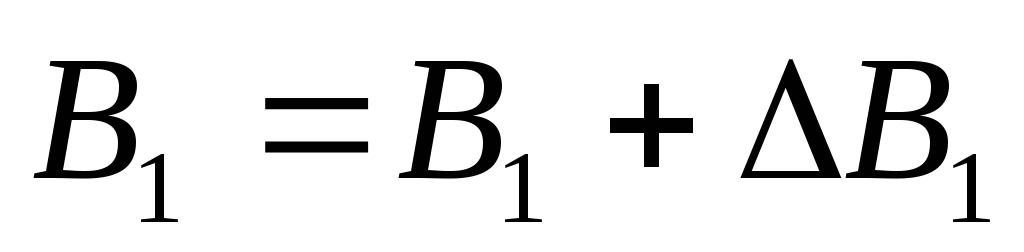 ,
,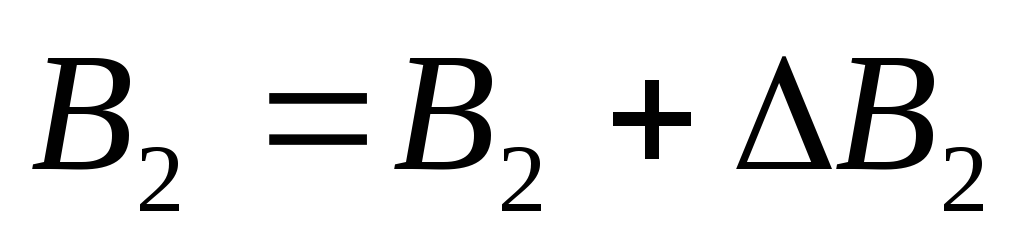 .
.Сравнить величины
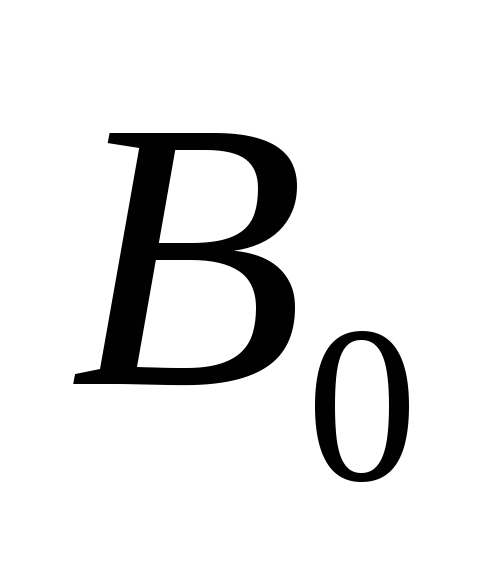 ,
, ,
,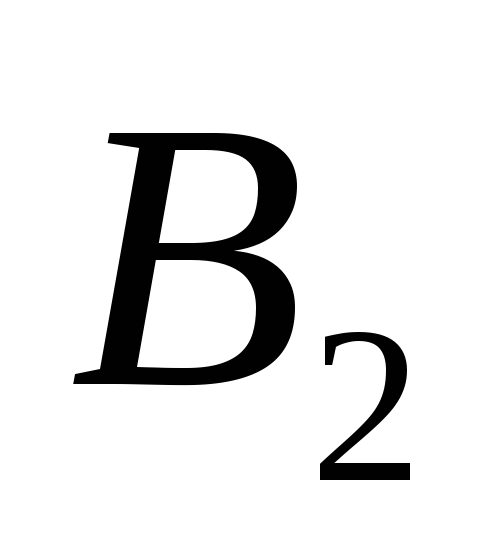 и сделать вывод о формуле (7.2).
и сделать вывод о формуле (7.2).
Задание 2. Определение универсальной газовой постоянной
Обработка результатов и расчёт погрешностей.
Величину газовой постоянной для двух случаев j 1,2 рассчитать по формуле
![]() ,
(7.5)
,
(7.5)
считая,
что величины
![]() и
и![]() являются приборными константами.
являются приборными константами.
Погрешность
 вычислить с учётом зависимости (7.4) по
формуле
вычислить с учётом зависимости (7.4) по
формуле
![]() .(7.6)
.(7.6)
Результат представить в виде
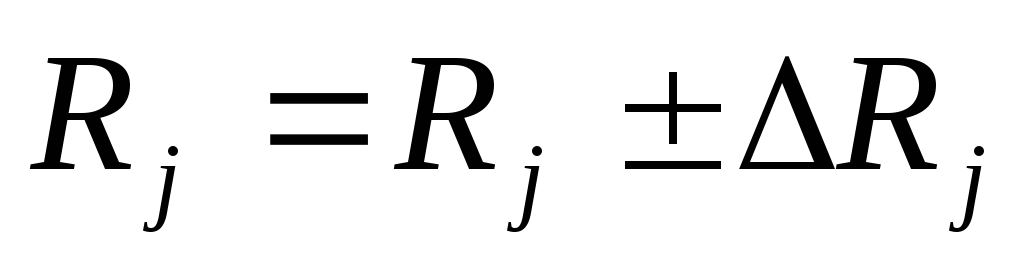 ,j=1,2.
,j=1,2.Сравнить величины
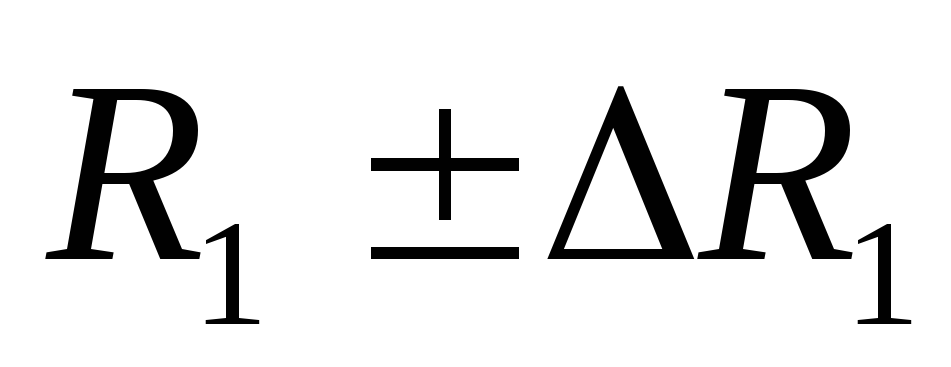 и
и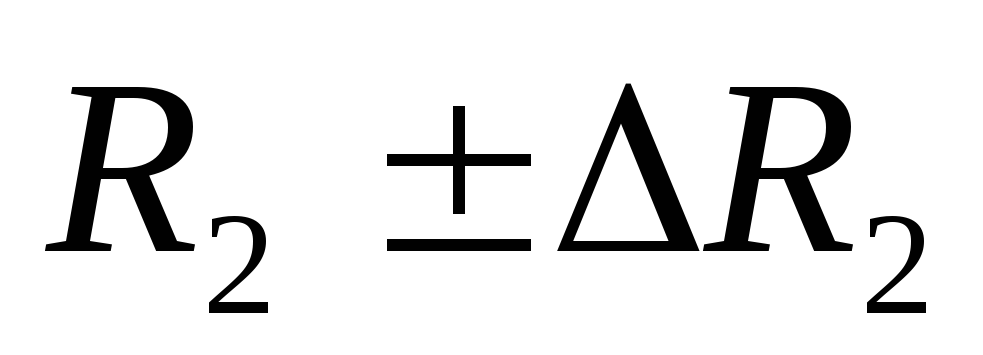 с табличным значениемR.
с табличным значениемR.
Задание 3. Определение газовой постоянной методом измерения объема и давления паров жидкости.
Если в сосуд известного объема ввести определенную массу легко испаряющейся жидкости, а после того, как она полностью испарится, измерить, насколько увеличится давление внутри сосуда, то, зная молекулярную массу жидкости и температуру, можно вычислить Rпо формуле
![]() (7.7)
(7.7)
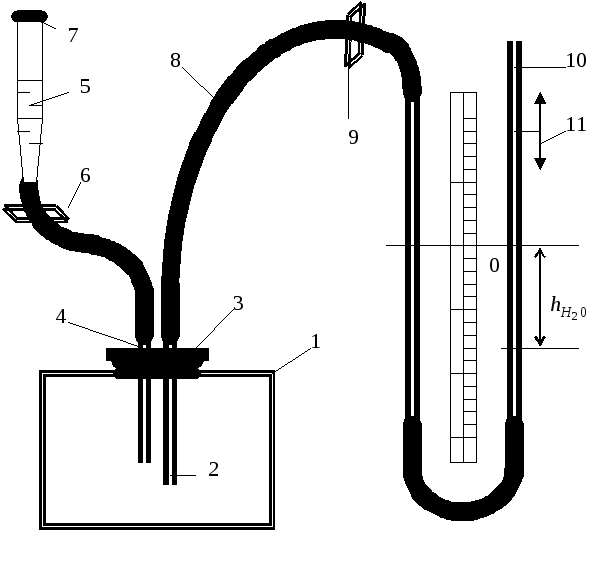
У
Рис. 7.3 Схема
экспериментальной
установки
В
сосуд вводится ацетон из микробюретки:
![]() ац=
0,058
кг/моль,
ац=
0,058
кг/моль,
![]() 790
кг/м3,
790
кг/м3,
![]() ,
(7.8)
,
(7.8)
где Vац – объем ацетона, введенного в сосуд.
Так как парциальное давление паров ацетона измеряется водяным манометром по разности уровней воды в его коленах, то
![]() (7.9)
(7.9)
где ![]() разность
уровней воды в коленах манометра.
разность
уровней воды в коленах манометра.
Учитывая (7.8) и (7.9), можно записать
![]() (7.10)
(7.10)
Первый сомножитель в (7.8) является величиной постоянной, второй − постоянен для конкретных условий проведения опыта при постоянной температуре и объеме сосуда. Таким образом определение R сводится к измерению объема жидкого ацетона, введенного в сосуд, и разности уровней воды в коленах манометра, обусловленной давлением паров ацетона. Точный объем сосуда с учетом объема резинового шланга, соединяющего сосуд с манометром и объема трубки манометра до уровня нулевой отметки написан на стенке сосуда. Работа выполняется в такой последовательности:
1. Измеряется объем ацетона микробюретке.
2. Открывается кран у тройника 9 и перемещением правого колена манометра уровень воды устанавливается на нулевую отметку шкалы. После этого закрывается кран 9.
3. Весь ацетон из микробюретки выливается в сосуд, в результате чего изменяются показания манометра. После того, как весь ацетон испарится, показания манометра перестанут изменяться.
4. Передвижением правого колена манометра устанавливается уровень воды в левом колене на нулевую отметку. Это необходимо сделать для сохранения объема воздуха в сосуде и трубках таким же, как в начале опыта. Тогда манометр покажет только парциальное давление паров ацетона, так как температура не изменилась.
5. По шкале манометра отсчитывается разность уровней воды и в его коленах и данные записываются в таблицу.
Обработка результатов
1. Газовая постоянная вычисляется по формуле (7.11).
2.
Так как измеряется только одна переменная
![]() один раз, то предельная погрешность
косвенных измерений величиныR
определяется по формуле
один раз, то предельная погрешность
косвенных измерений величиныR
определяется по формуле
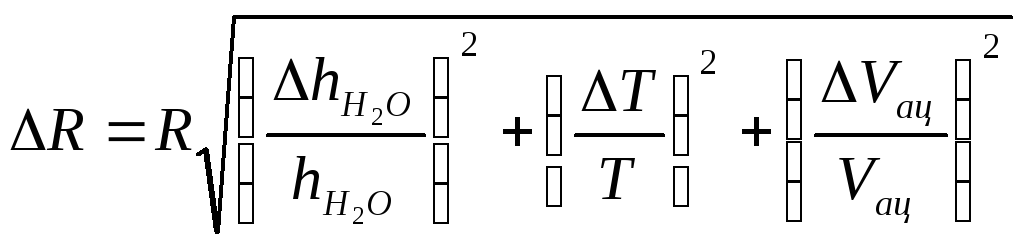 ,
(7.11)
,
(7.11)
где
![]() ,
,![]() и
и![]() − систематические погрешности определения
разности уровней в манометре после
испарения ацетона, температуры и объёма
ацетона.
− систематические погрешности определения
разности уровней в манометре после
испарения ацетона, температуры и объёма
ацетона.
3. Сравниваются величины газовой постоянной, полученные разными методами, и погрешности этих методов.
4.
Если измерения проводятся несколько
раз, то процедура расчёта погрешностей
несколько отличается. В этом случае при
измерениях изменяются две величины:
![]() ,
,![]() .
Поэтому
.
Поэтому
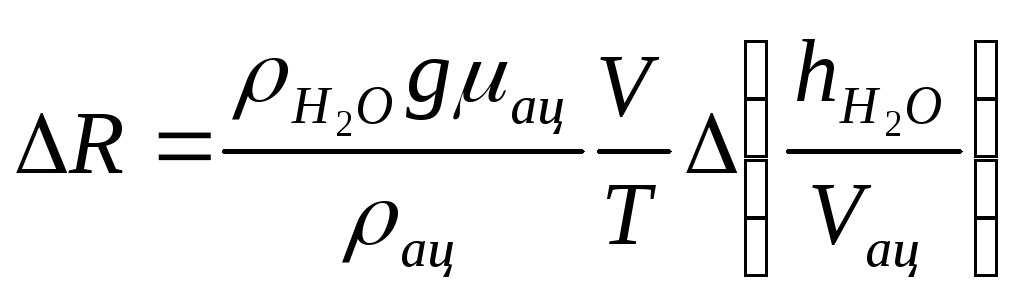 ,
(7.12)
,
(7.12)
где
погрешность величины
![]() /
/![]() необходимо определить по методике
расчёта погрешностей прямых многократных
измерений, задавая доверительную
вероятность
необходимо определить по методике
расчёта погрешностей прямых многократных
измерений, задавая доверительную
вероятность![]() и коэффициент Стьюдента.
и коэффициент Стьюдента.
Лабораторная работа 8
