Вариант 10.
Задание 1. Найти производную скалярного поля в точке по направлению нормали к поверхности , образующей острый угол с положительным направлением оси :
,
, 
.
Задание 2. Найти градиент скалярного поля и построить поверхности уровня для заданных значений :
, 
.
Задание 3. Найти векторные линии векторного поля :
.
Задание 4. Найти поток векторного
поля
через
боковую поверхность и верхнее основание параллелепипеда, ограниченного плоскостями
;сечение параллелепипеда плоскостью
в направлении нормали, образующей
острый угол с осью
.
Задание 5. Найти поток векторного
поля
через плоскость
,
расположенную в первом октанте (нормаль
образует острый угол с осью Oz).
Задание 6. Найти поток векторного
поля
через часть поверхности параболоида
,
вырезанной конусом
.
Задание 7. Найти работу силы
,
при перемещении материальной точки
вдоль линии
от точки
до точки
.
Задание 8. Найти циркуляцию векторного
поля
вдоль контура
в направлении, соответствующем возрастанию
параметра
.
Задание 9. Найти циркуляцию векторного
поля
по контуру
непосредственно и по формуле Стокса.
Задание10. Показать потенциальность
векторного поля
.
Найти его потенциал.
Задание 11. Найти
и
векторного поля
,
где
‑ радиус-вектор точки.
Вариант 11.
Задание 1. Найти производную скалярного поля в точке по направлению нормали к поверхности , образующей острый угол с положительным направлением оси :
,
, 
.
Задание 2. Найти градиент скалярного поля и построить поверхности уровня для заданных значений :
,
где
‑ радиус-вектор точки поля, 
.
Задание 3. Найти векторные линии векторного поля :
.
Задание 4. Найти поток вихрей вектора
через
боковую поверхность цилиндра
,
стоящего на плоскости
;сечение этого цилиндра плоскостью в направлении нормали, образующей острый угол с осью .
Задание 5. Найти поток векторного
поля
через плоскость
,
расположенную в первом октанте (нормаль
образует острый угол с осью Oz).
Задание 6. Найти поток векторного
поля
через замкнутую поверхность
.
Задание 7. Найти работу силы
,
при перемещении материальной точки
вдоль линии
от точки
до точки
.
Задание 8. Найти циркуляцию
векторного поля
вдоль контура
в направлении, соответствующем возрастанию
параметра
.
Задание 9. Найти циркуляцию
векторного поля
по контуру
непосредственно и по формуле Стокса.
Задание10. Показать потенциальность
векторного поля
.
Найти его потенциал.
Задание 11. Пусть
- произвольные дважды дифференцируемые
функции. Доказать, что
.
Вариант 12.
Задание 1. Найти производную скалярного поля в точке по направлению нормали к поверхности , образующей острый угол с положительным направлением оси :
,
, 
.
Задание 2. Найти градиент скалярного поля и построить поверхности уровня для заданных значений :
, 
.
Задание 3. Найти векторные линии векторного поля :
.
Задание 4. Найти поток поля вектора через
полную поверхность тела, ограниченного параболоидом
и плоскостью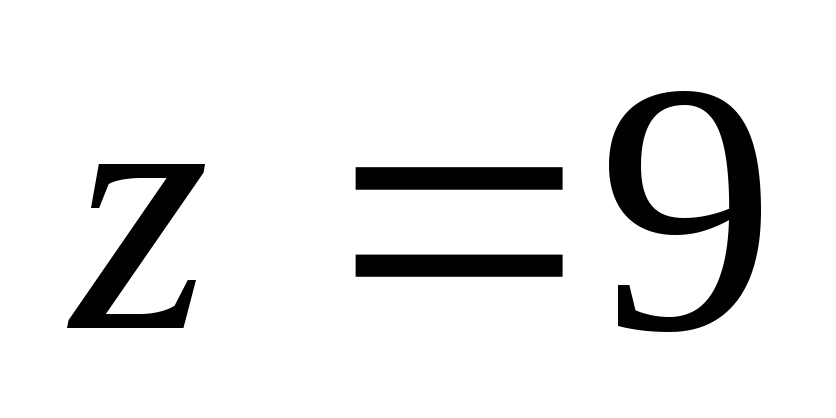
;площадь круга , в отрицательном направлении оси .
Задание 5. Найти поток векторного
поля
через плоскость
,
расположенную в первом октанте (нормаль
образует острый угол с осью Oz).
Задание 6. Вычислить поток векторного
поля
через боковую поверхность пирамиды,
имеющей основание на плоскости
и вершины в точках
в направлении внешней нормали.
Задание 7. Найти работу силы
,
при перемещении материальной точки
вдоль линии
от точки
до точки
.
Задание 8. Найти циркуляцию
векторного поля
вдоль контура
в направлении, соответствующем возрастанию
параметра
.
Задание 9. Найти циркуляцию
векторного поля
по контуру
непосредственно и по формуле Стокса.
Задание10. Показать потенциальность
векторного поля
.
Найти его потенциал.
Задание 11. Найти
,
где
- произвольная дважды дифференцируемая
функция,
- радиус-вектор точки.