
- •Федеральное агентство по образованию
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
Вариант 21
Изменить порядок интегрирования в повторном интеграле
 .
.Вычислить двойной интеграл
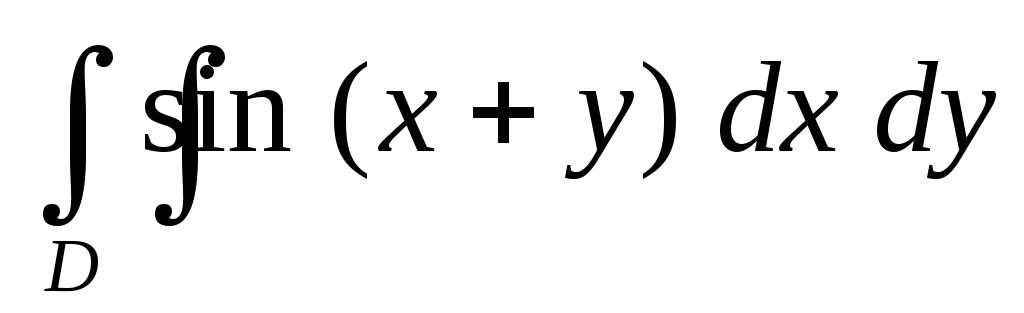 по областиD, ограниченной
линиями
по областиD, ограниченной
линиями .
.Найти массу пластинки, ограниченной лемнискатой Бернулли
 ,
плотность которой в каждой точке равна
квадрату расстояния ее до начала
координат.
,
плотность которой в каждой точке равна
квадрату расстояния ее до начала
координат.Вычислить объем тела V, ограниченного поверхностями
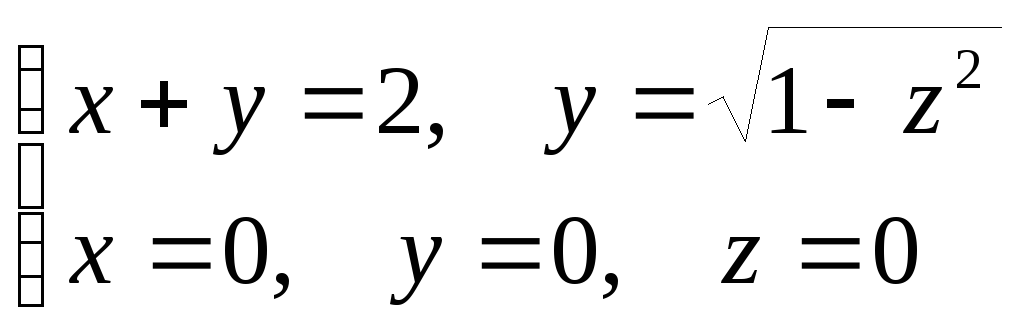 .
Плотность телаVсчитать
равной единице.
.
Плотность телаVсчитать
равной единице.Вычислить интеграл
 .
.Вычислить тройной интеграл
 ,
если областьVограничена
поверхностями
,
если областьVограничена
поверхностями .
.Найти массу тела, ограниченного поверхностями
 с плотностью
с плотностью .
.Вычислить криволинейный интеграл первого рода
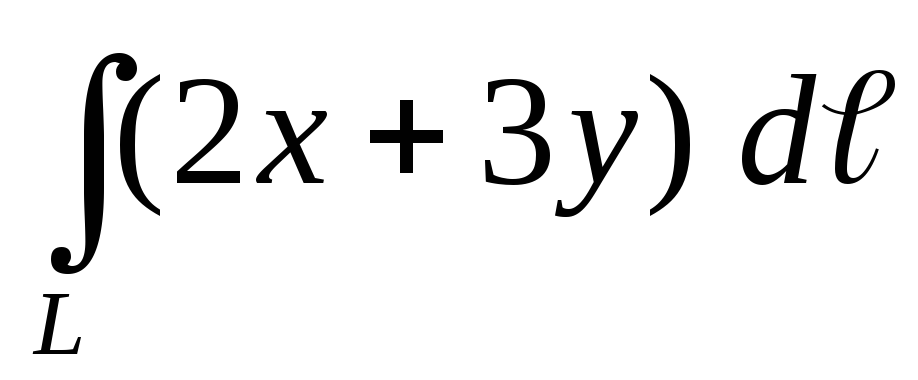 ,
еслиL– дуга циклоиды
,
еслиL– дуга циклоиды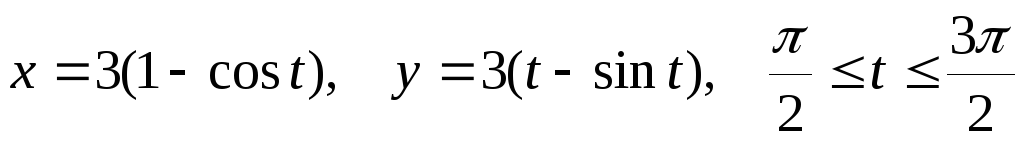 .
.Найти массу дуги линии
 от точки, соответствующей
от точки, соответствующей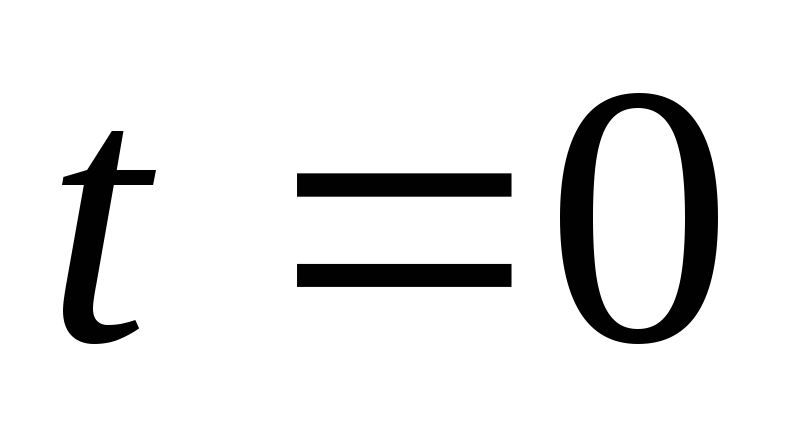 до
до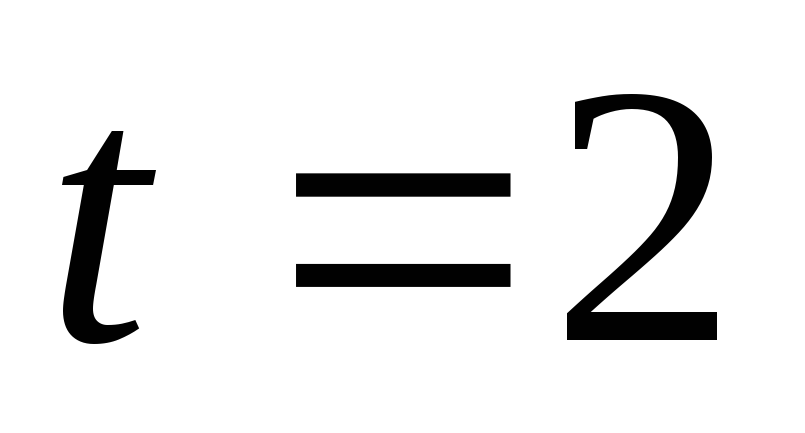 ,
если плотность дуги обратно пропорциональна
квадрату полярного радиуса и в точке
(1,0,1) равна 2.
,
если плотность дуги обратно пропорциональна
квадрату полярного радиуса и в точке
(1,0,1) равна 2.Вычислить криволинейный интеграл второго рода
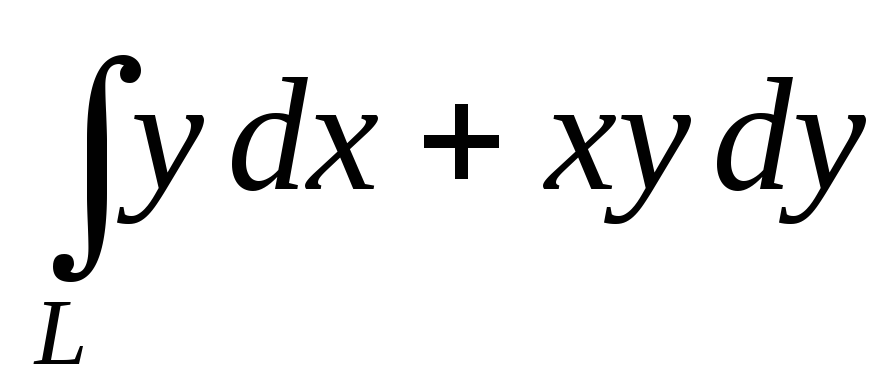 ,
гдеL– четверть дуги
эллипса с полуосями а=2, в=1, лежащая в
первой координатной четверти при
положительном направлении обхода.
,
гдеL– четверть дуги
эллипса с полуосями а=2, в=1, лежащая в
первой координатной четверти при
положительном направлении обхода.Вычислить криволинейный интеграл
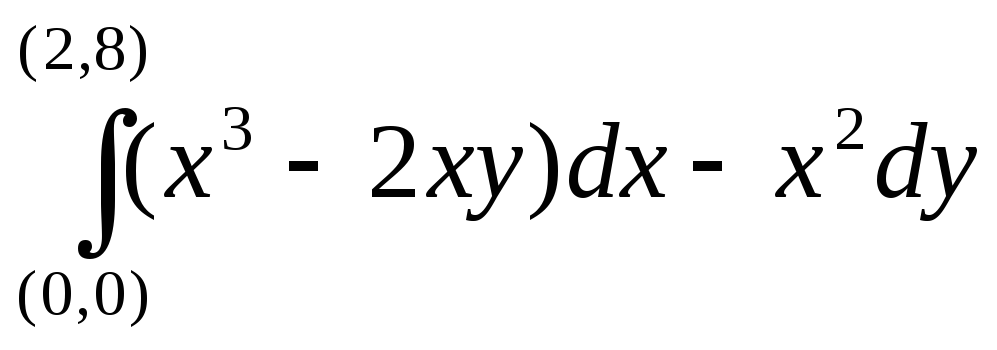 по прямой
по прямой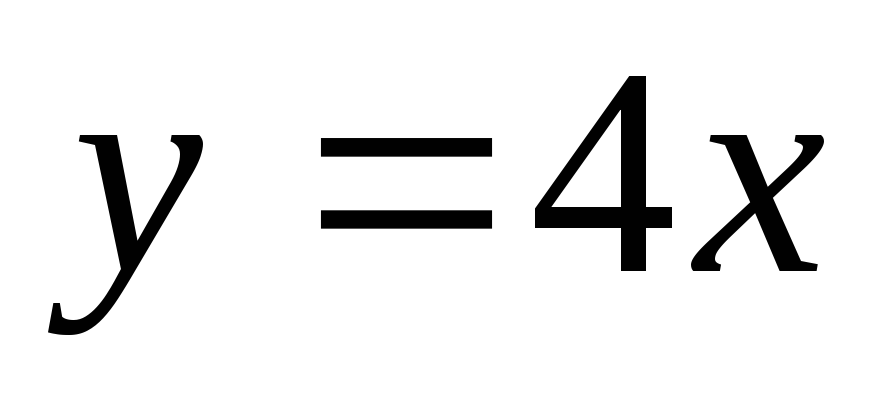 и по дуге параболы
и по дуге параболы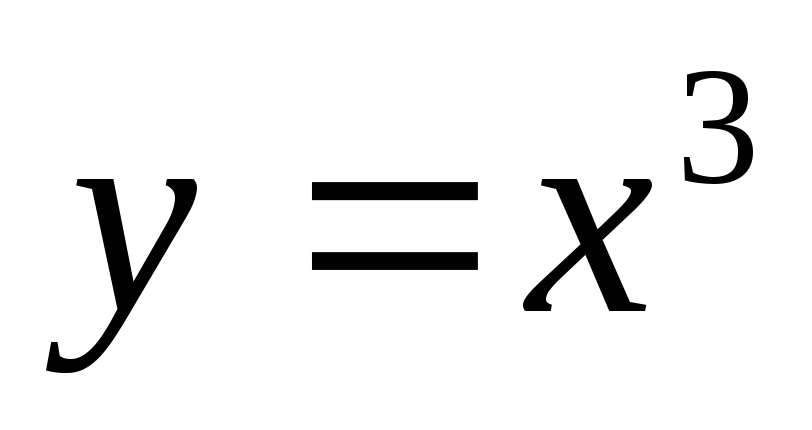 .
.Вычислить поверхностный интеграл первого рода
 по пространственной области
по пространственной области
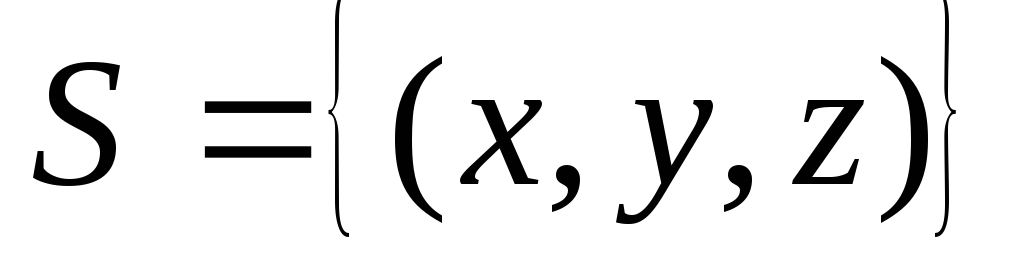 ,
определяемой условиями
,
определяемой условиями .
.Вычислить поверхностный интеграл второго рода
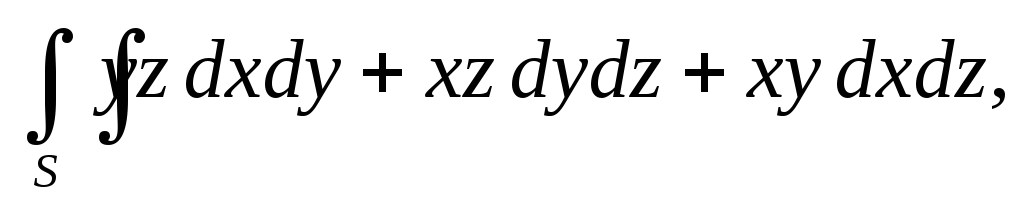 гдеS– внешняя сторона
поверхности, расположенной в первом
октанте и составленной из цилиндра
гдеS– внешняя сторона
поверхности, расположенной в первом
октанте и составленной из цилиндра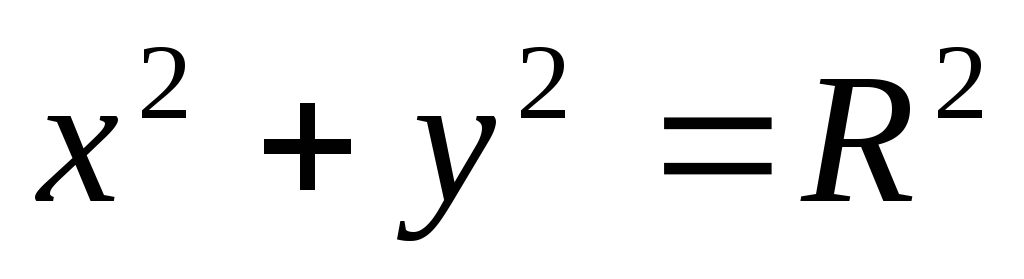 и плоскостей
и плоскостей и
и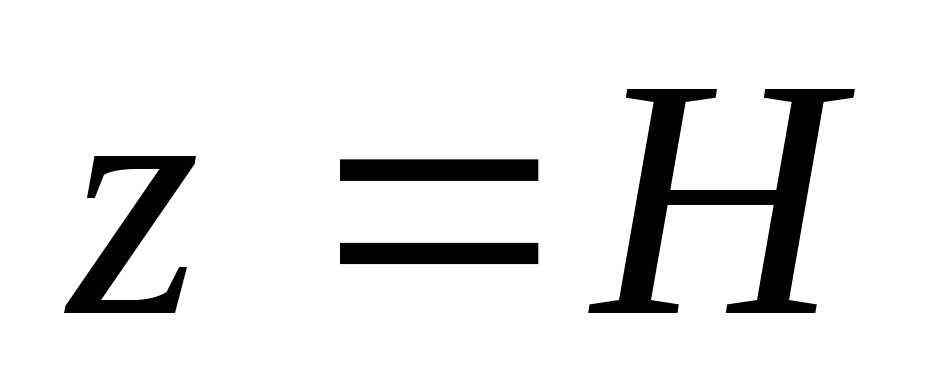 .
.
Вариант 22
Изменить порядок интегрирования в повторном интеграле
 .
.Вычислить двойной интеграл
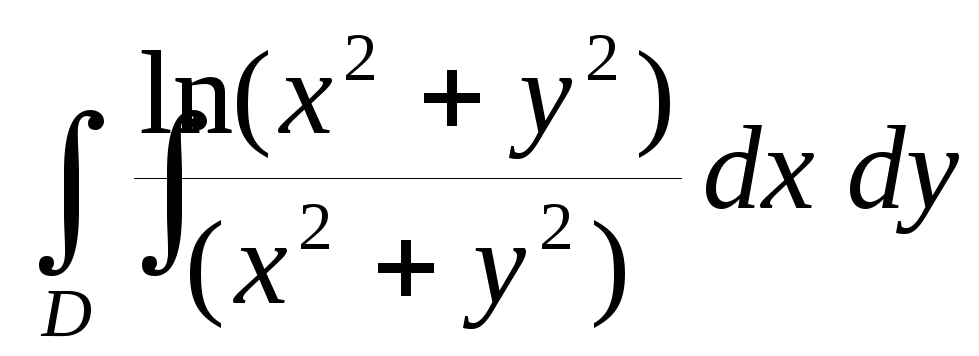 по областиD, ограниченной
окружностями
по областиD, ограниченной
окружностями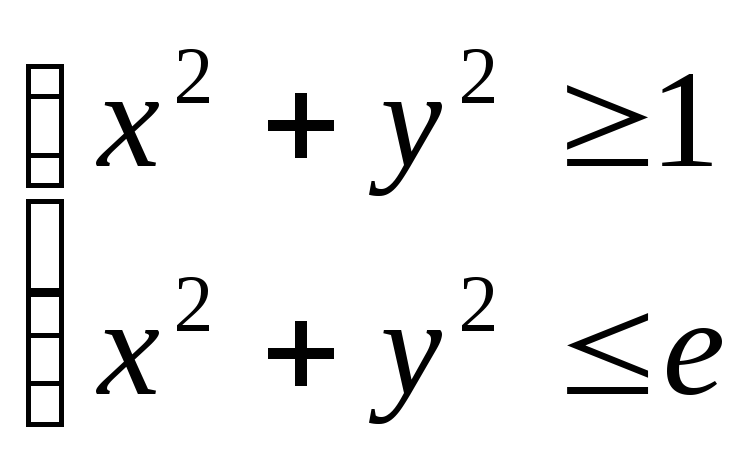 .
.Найти момент инерции относительно оси Oх плоской фигуры, ограниченной линиями:
 .
.Вычислить объем тела V, ограниченного поверхностями
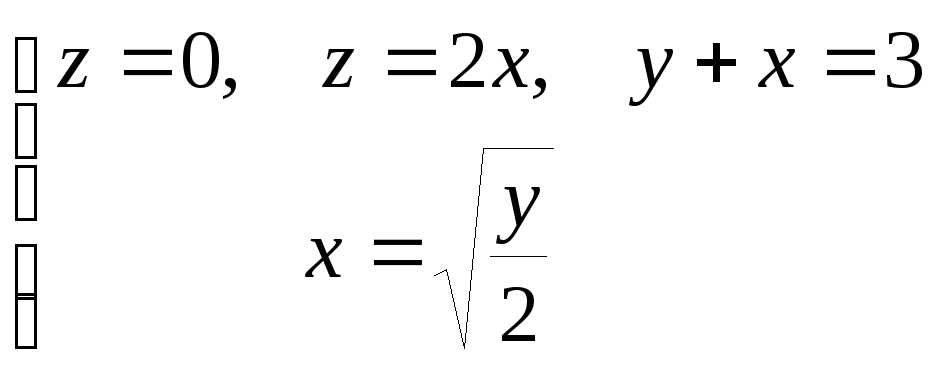 .
Плотность телаVсчитать
равной единице.
.
Плотность телаVсчитать
равной единице.Вычислить тройной интеграл
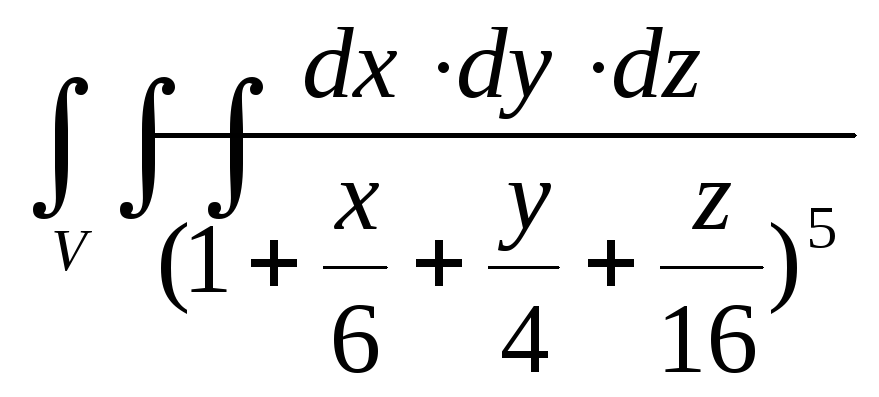 ,
если областьVограничена
плоскостями
,
если областьVограничена
плоскостями .
.Вычислить тройной интеграл
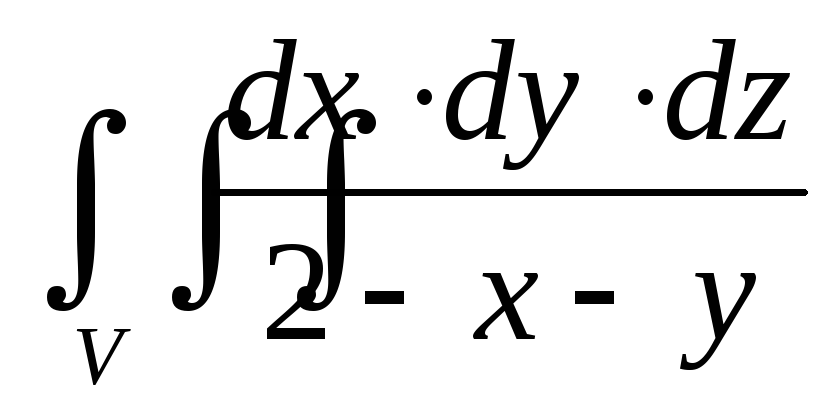 ,
если областьVограничена
поверхностями
,
если областьVограничена
поверхностями .
.Найти массу тела, ограниченного поверхностями
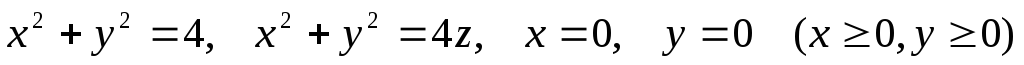 с плотностью
с плотностью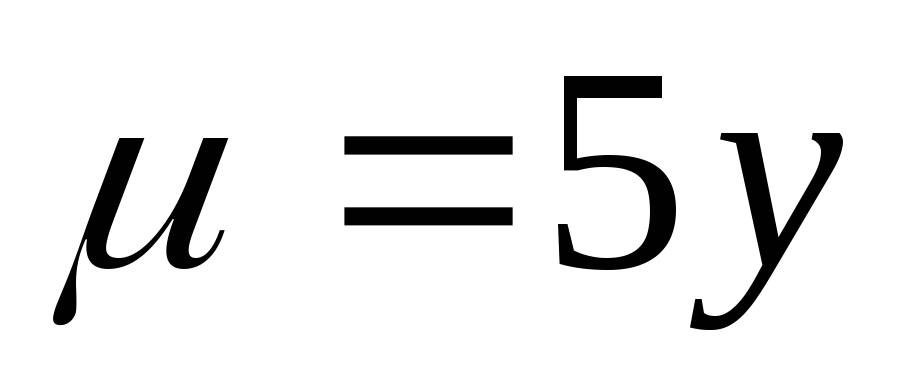 .
.Вычислить криволинейный интеграл первого рода
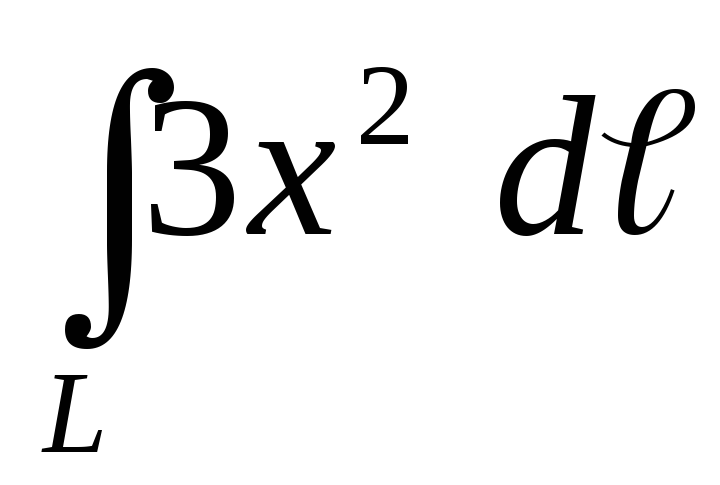 ,
еслиL– дуга кривой
,
еслиL– дуга кривой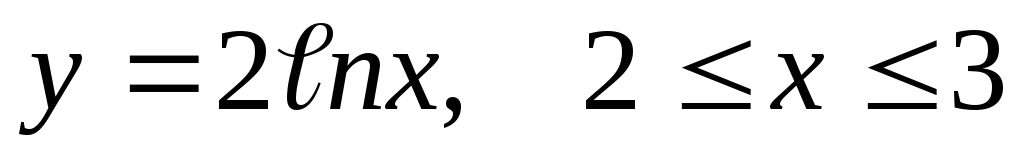 .
.Найти координаты центра масс первого полувитка винтовой линии
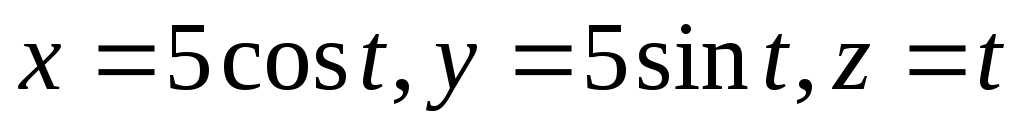 ,
считая плотность равной 3.
,
считая плотность равной 3.Вычислить криволинейный интеграл второго рода
 ,
гдеL– верхняя полуокружность
,
гдеL– верхняя полуокружность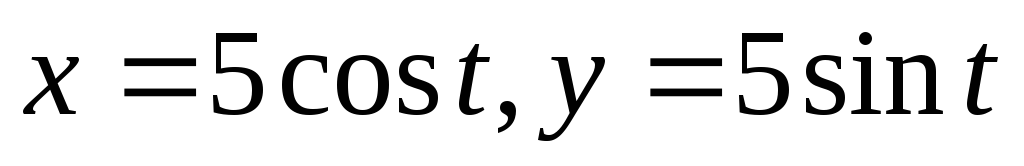 при положительном направлении обхода.
при положительном направлении обхода.С помощью криволинейного интеграла найти площадь, ограниченную кардиоидой
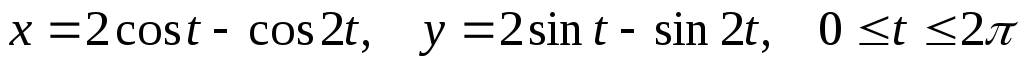 .
.Вычислить поверхностный интеграл первого рода
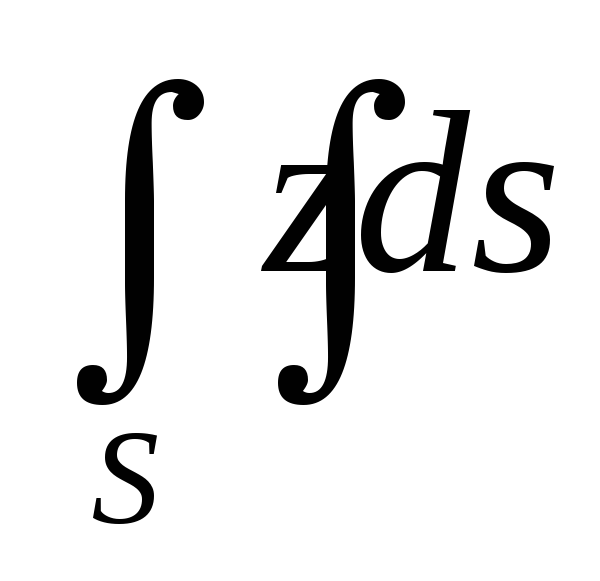 по пространственной области
по пространственной области
 ,
определяемой условиями
,
определяемой условиями .
.Вычислить поверхностный интеграл второго рода
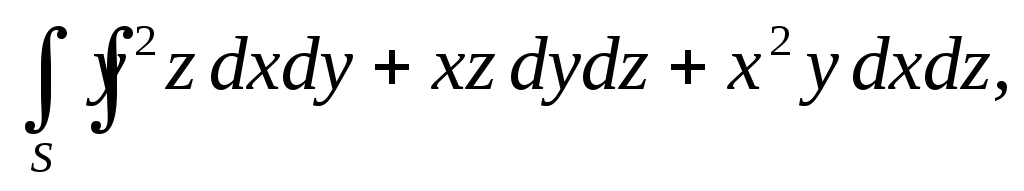 гдеS– внешняя сторона
поверхности, расположенной в первом
октанте и составленной из параболоида
вращения
гдеS– внешняя сторона
поверхности, расположенной в первом
октанте и составленной из параболоида
вращения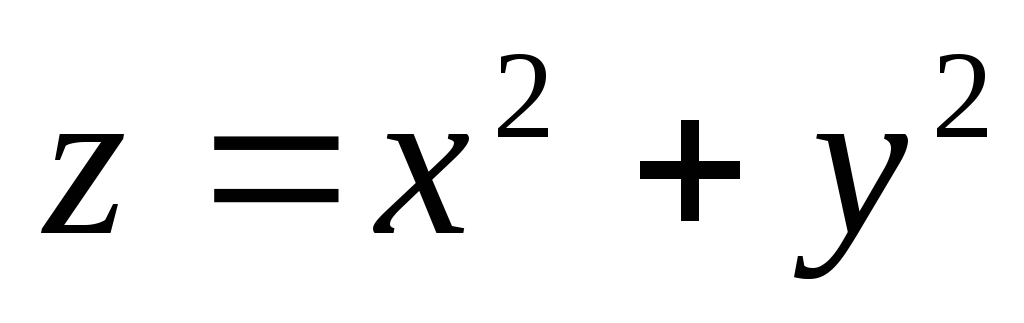 ,
цилиндра
,
цилиндра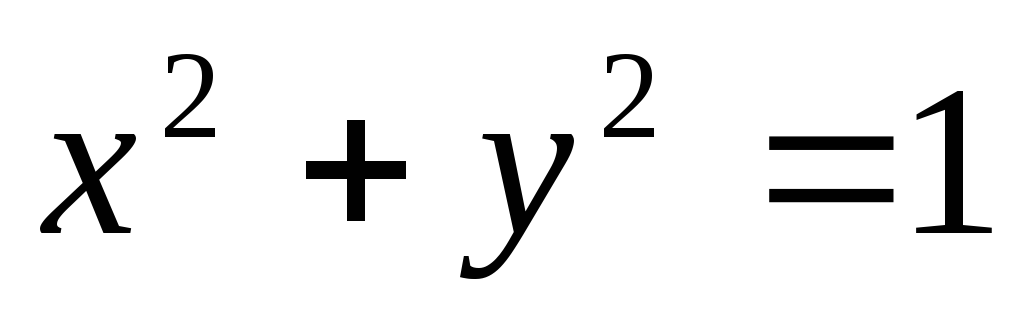 и координатных плоскостей.
и координатных плоскостей.
Вариант 23
Изменить порядок интегрирования в повторном интеграле
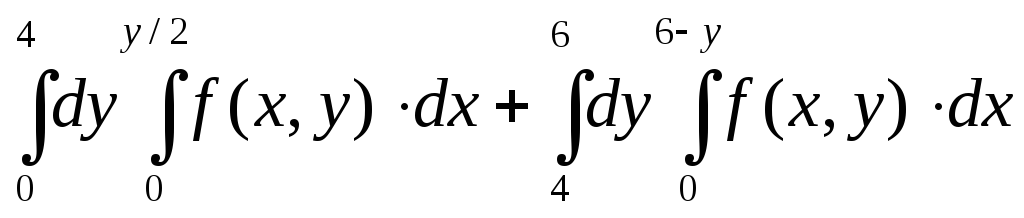 .
.Вычислить двойной интеграл
 по областиD, определяемой
условием
по областиD, определяемой
условием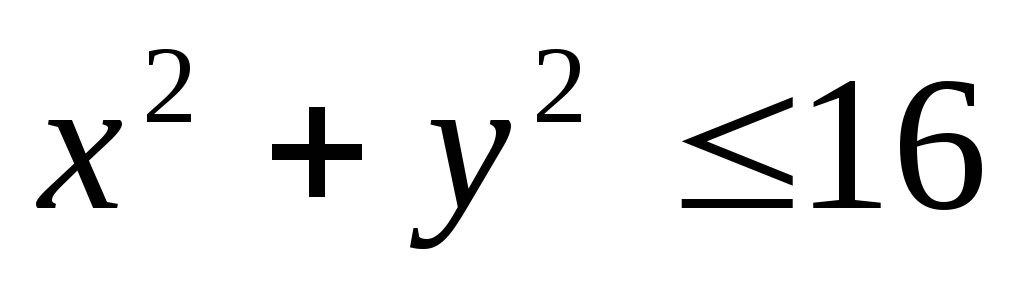 .
.Определить момент инерции относительно оси Oх однородной плоской фигуры, ограниченной линиями:
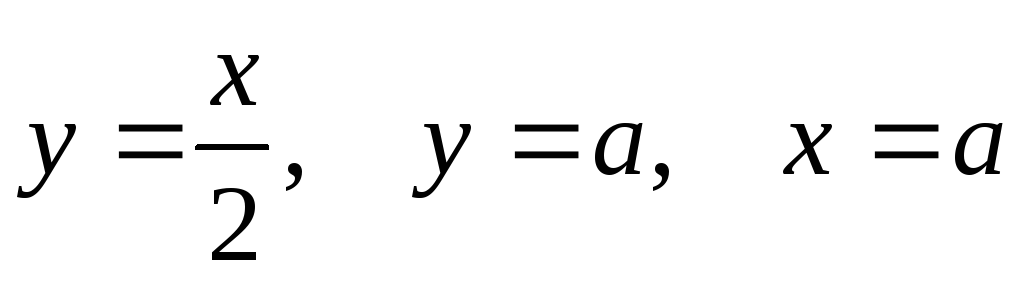 .
.Вычислить объем тела V, ограниченного поверхностями
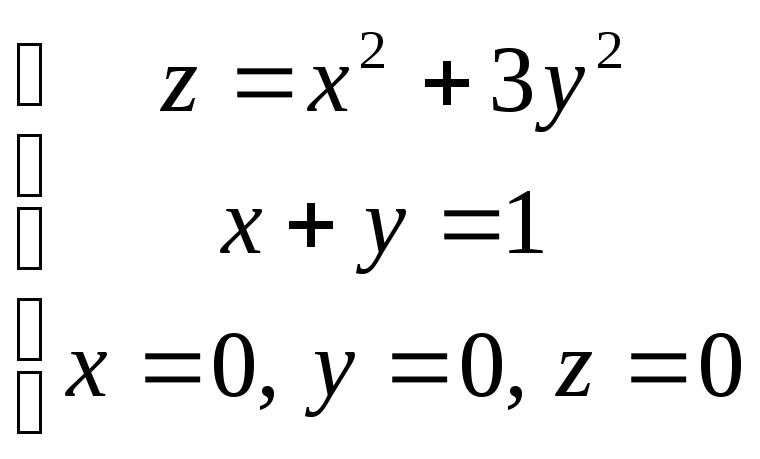 .
Плотность телаVсчитать
равной единице.
.
Плотность телаVсчитать
равной единице.Вычислить тройной интеграл
 по областиV, определяемой
уравнениями
по областиV, определяемой
уравнениями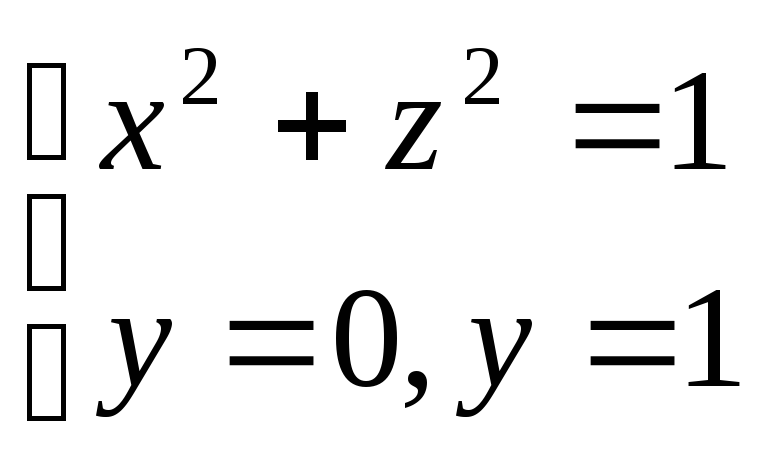 .
.Вычислить тройной интеграл
 ,
если областьVограничена
поверхностями
,
если областьVограничена
поверхностями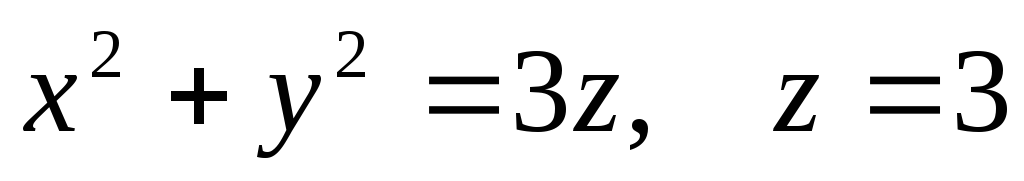 .
.Найти массу тела, ограниченного поверхностями
 с плотностью
с плотностью .
.Вычислить криволинейный интеграл первого рода
 ,
еслиL– дуга кривой
,
еслиL– дуга кривой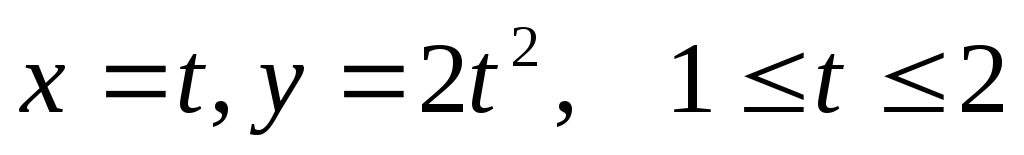 .
.Вычислить статический момент первого витка винтовой линии
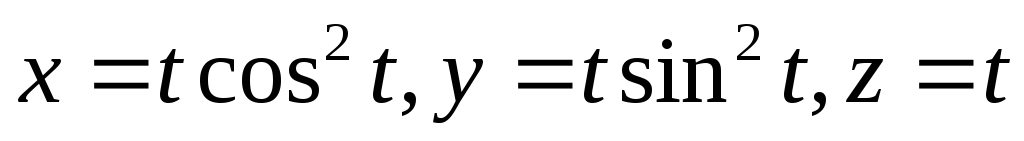 ,
относительно плоскости Оxy,
считая плотность пропорциональной
квадрату расстояния от этой плоскости
,
относительно плоскости Оxy,
считая плотность пропорциональной
квадрату расстояния от этой плоскости .
.Вычислить криволинейный интеграл второго рода
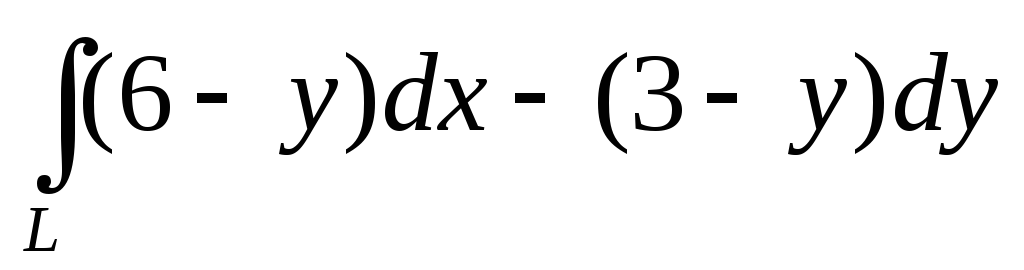 ,
гдеL– арка циклоиды
,
гдеL– арка циклоиды .
.Найти работу силы
 от точки
от точки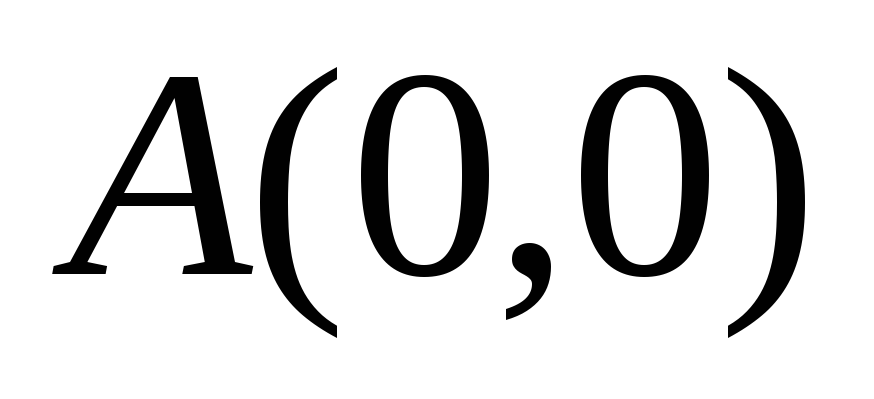 до точки
до точки вдоль дуги циклоиды
вдоль дуги циклоиды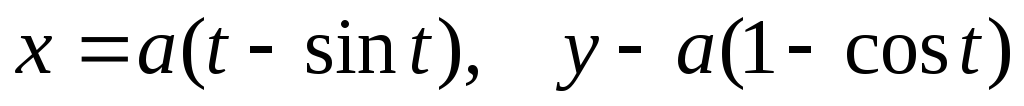 .
.Вычислить поверхностный интеграл первого рода
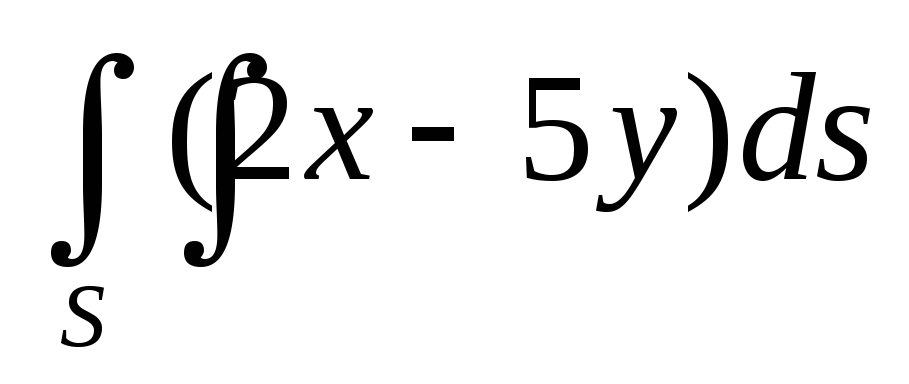 по пространственной области
по пространственной области
 ,
определяемой условиями
,
определяемой условиями .
.Вычислить интеграл
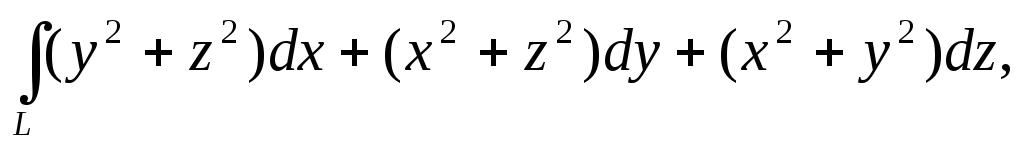 взятый по некоторому замкнутому контуру,
преобразовать с помощью формулы Стокса
в интеграл по поверхности, «натянутой»
на этот контур.
взятый по некоторому замкнутому контуру,
преобразовать с помощью формулы Стокса
в интеграл по поверхности, «натянутой»
на этот контур.
