Вариант 12

1. Изменить порядок интегрирования в повторном интеграле .

2. Вычислить двойной интеграл 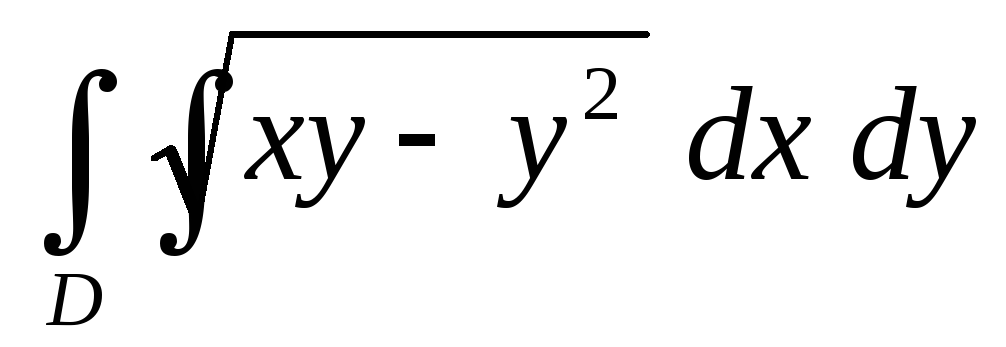по областиD, представляющей собой треугольник с вершинами О(0,0), А(10,1), В(1.1).

3. Вычислить площадь плоской пластины D, определяемой уравнением.

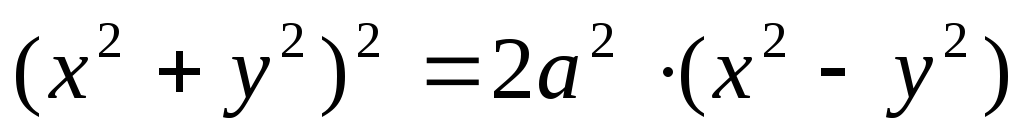4. Вычислить объем тела V, ограниченного поверхностями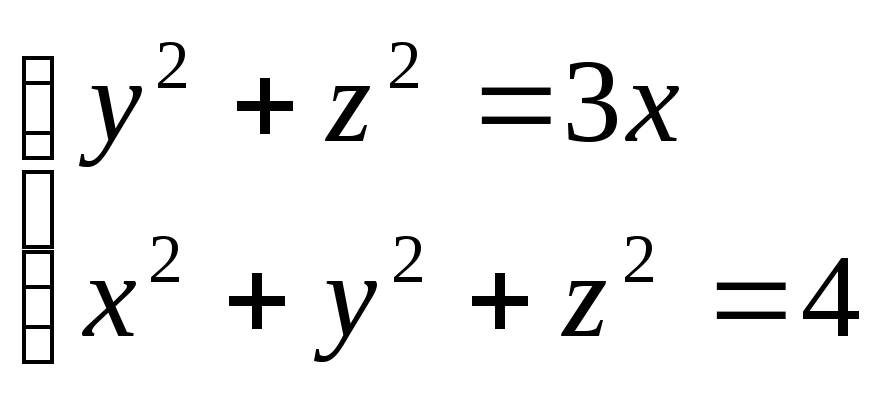. Плотность телаVсчитать равной единице.

5. Вычислить тройной интеграл 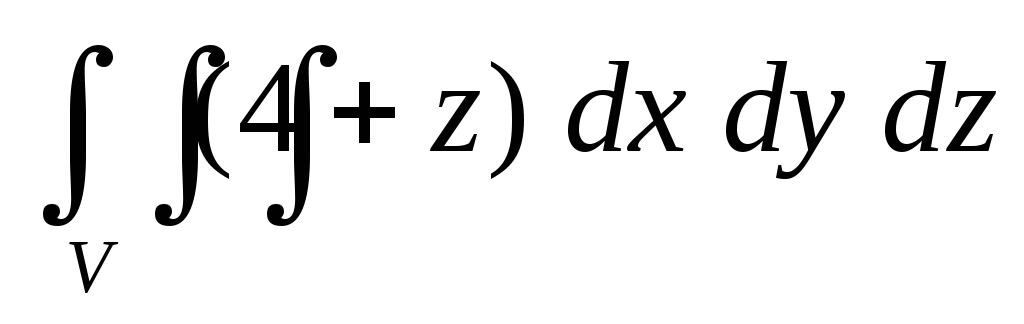по пространственной областиV, ограниченной поверхностями.

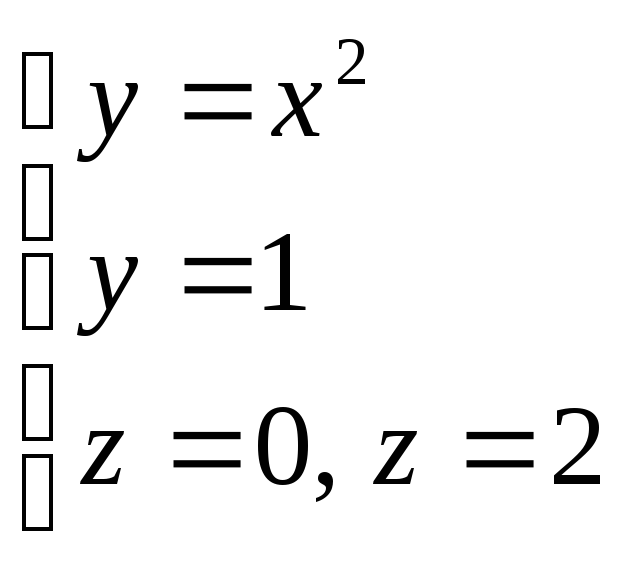6. Вычислить тройной интеграл 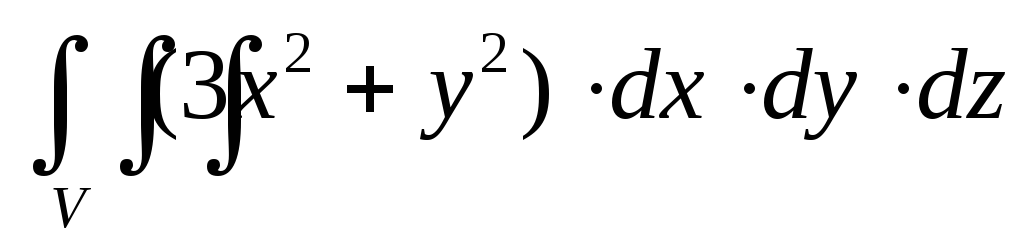, если областьVограничена плоскостями.

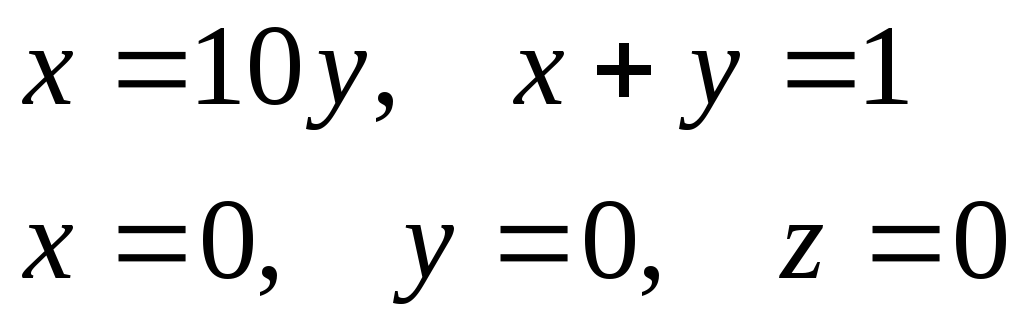7. Найти массу тела, ограниченного поверхностями 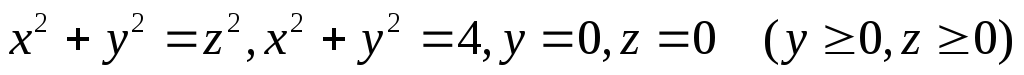, если плотность определяется по формуле.

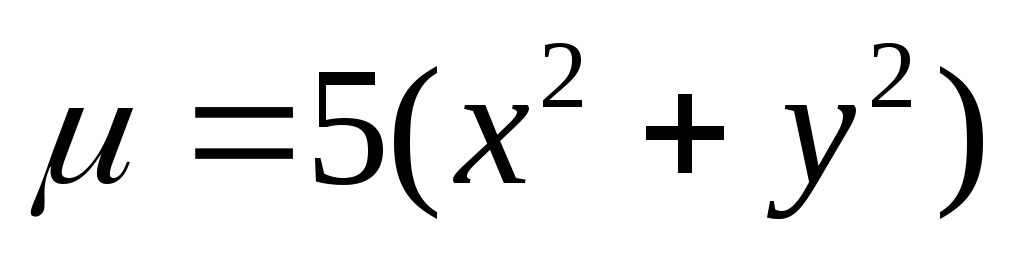8. Вычислить криволинейный интеграл первого рода по кривойL:.

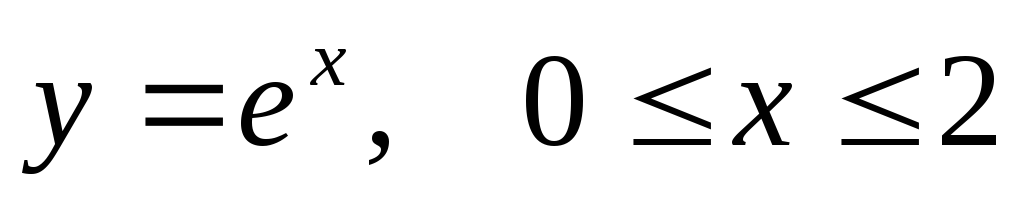9. Вычислить моменты инерции первого витка винтовой линии относительно координатной оси Оy.

10. Вычислить криволинейный интеграл второго род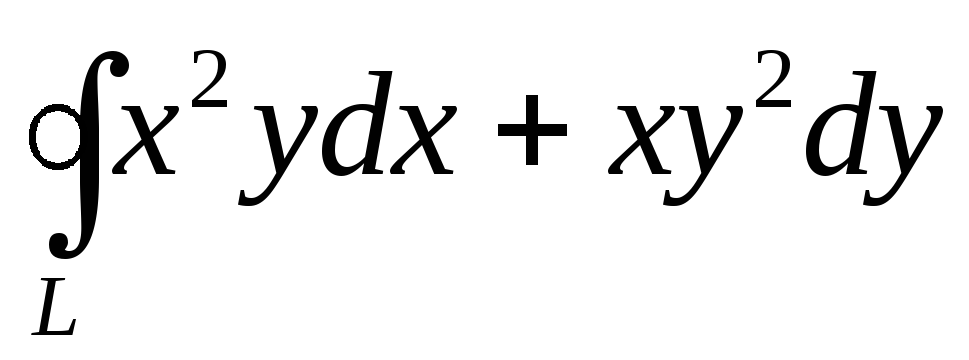а , гдеL– дуга эллипсапри положительном направлении обхода.

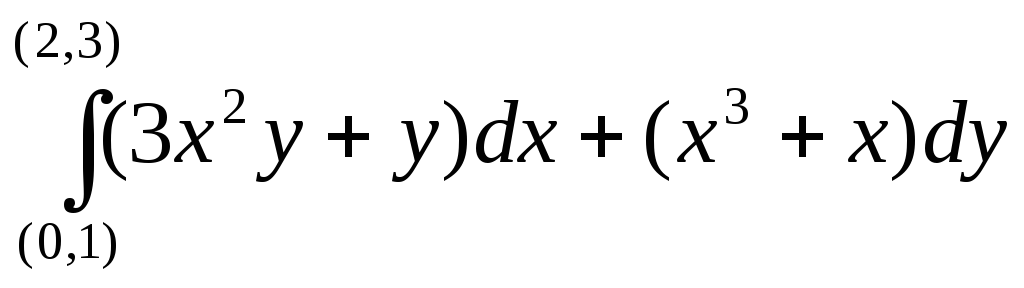11. Показать, что криволинейный интеграл не зависит от пути интегрирования и вычислить этот интеграл.

12. Вычислить поверхностный интеграл первого рода 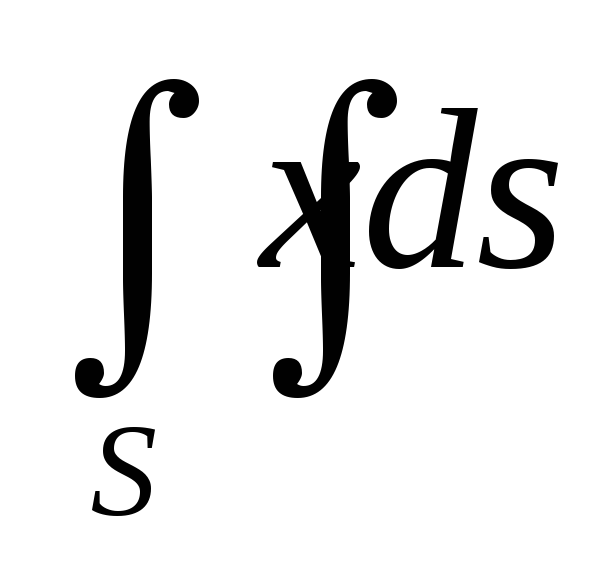по пространственной области, определяемой условиями.

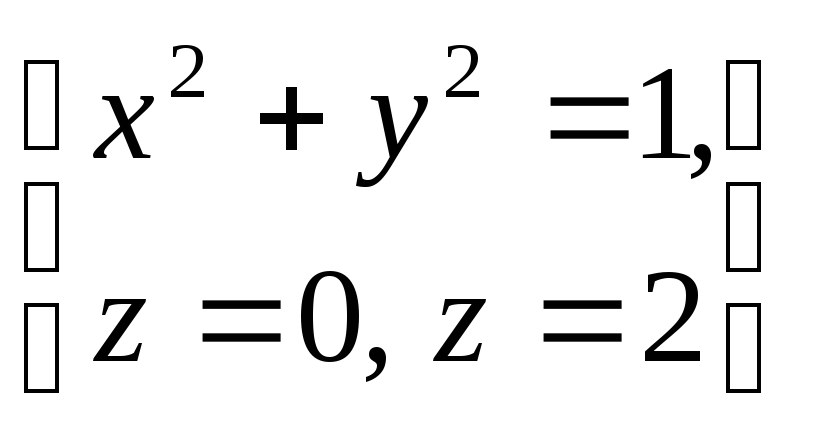13. Вычислить поверхностный интеграл второго ро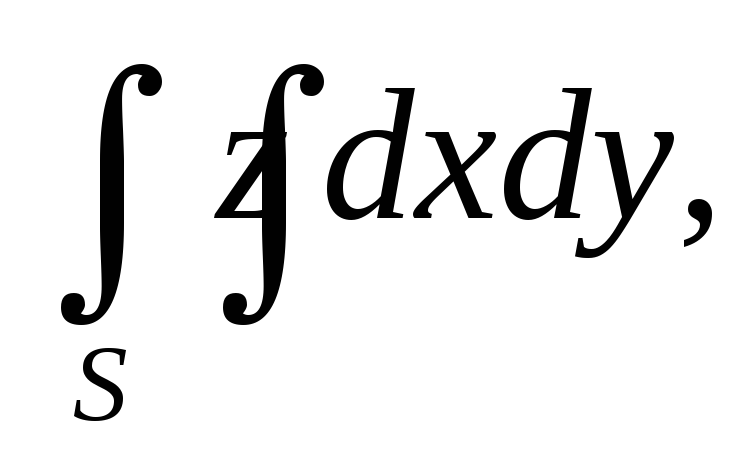да гдеS– внешняя сторона эллипсоида.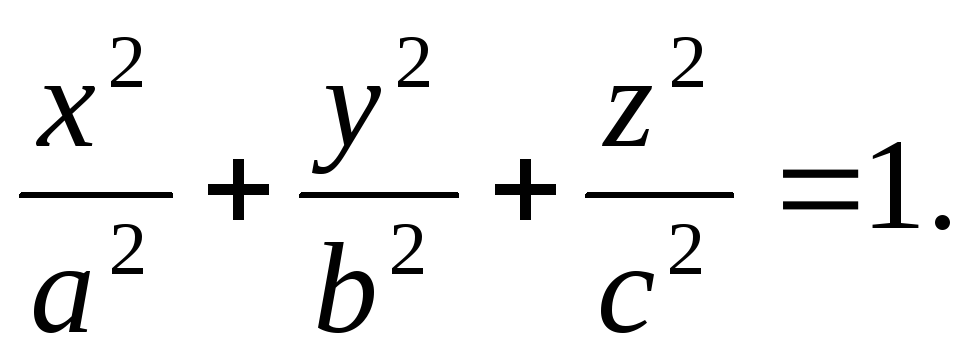

Вариант 13

1. Изменить порядок интегрирования в повторном интеграле .

2. Вычислить двойной интеграл 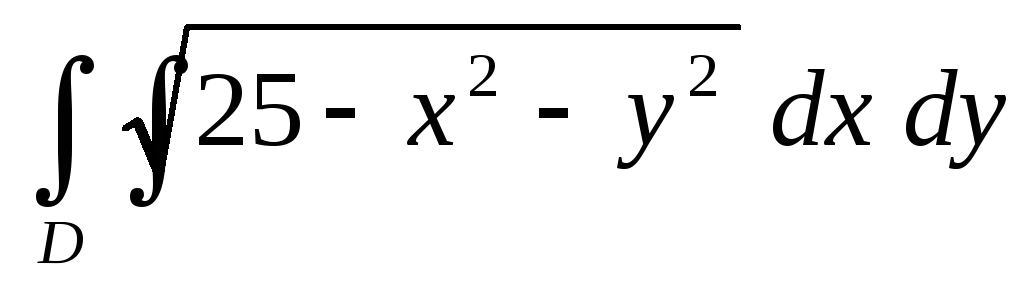по областиD, определяемой неравенством.

3. Определить центр тяжести однородной плоской пластинки, ограниченной линиями:

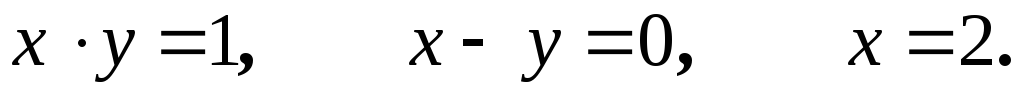
4. Вычислить объем тела V, ограниченного поверхностями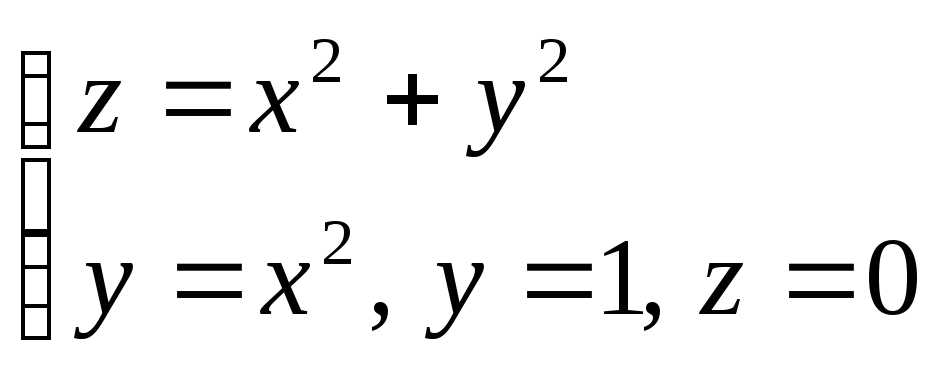. Плотность телаVсчитать равной единице.

5. Вычислить тройной интеграл 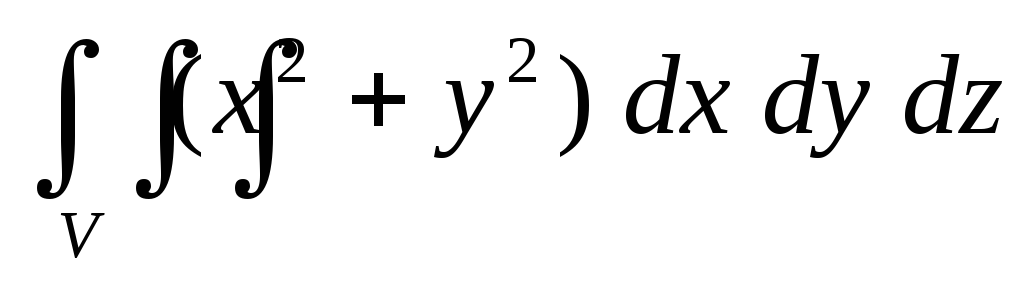по пространственной областиV, ограниченной поверхностями.

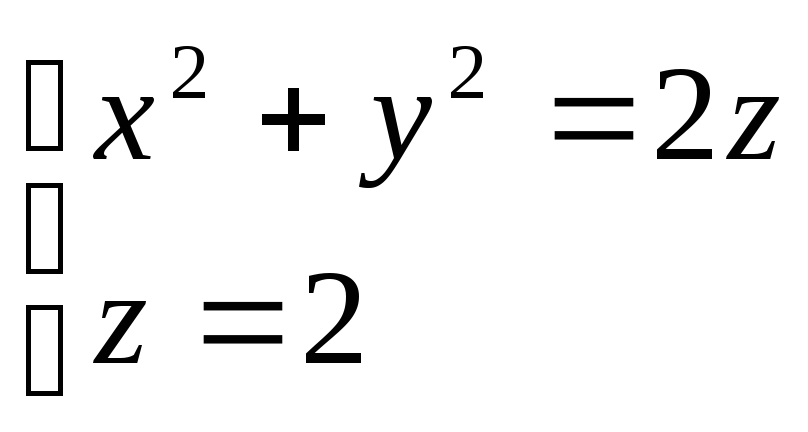6. Вычислить тройной интеграл 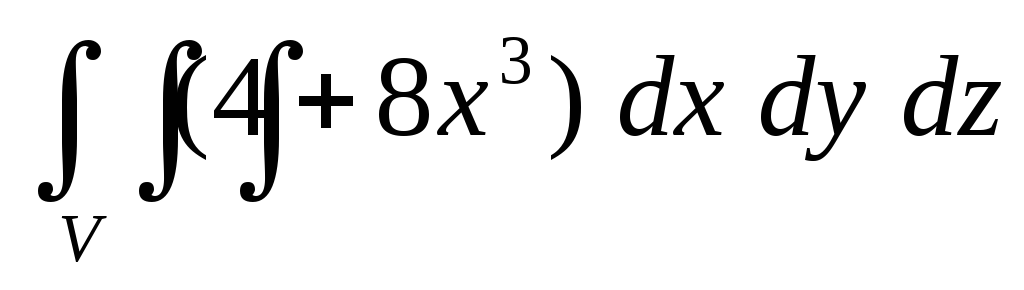, если областьVограничена поверхностями.

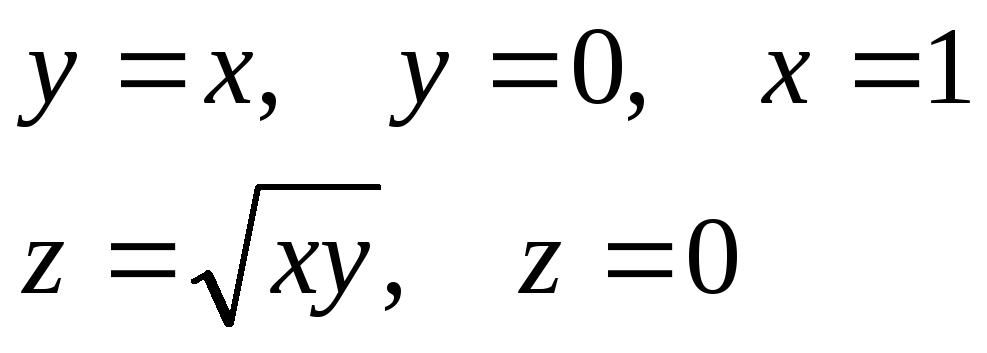7. Найти объем тела, определяемого неравенствами .

8. Вычислить криволинейный интеграл первого рода 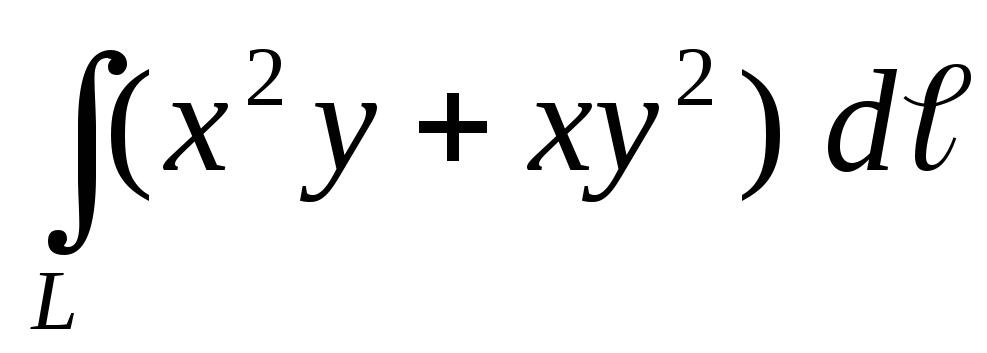по дугеLокружности, расположенной в первой координатной четверти.

9. Найти центр тяжести одной арки циклоиды 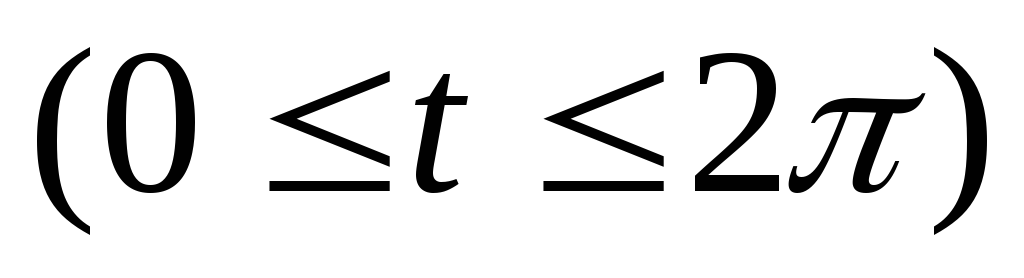. Считать плотность равной единице

10. Вычислить криволинейный интеграл второго рода , гдеL- дуга винтовой линии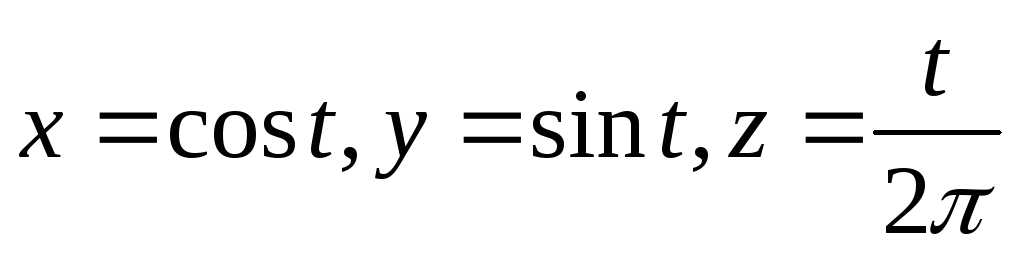от точки А(1,0,0) до точки В(1,0,1).

11. Найти функцию 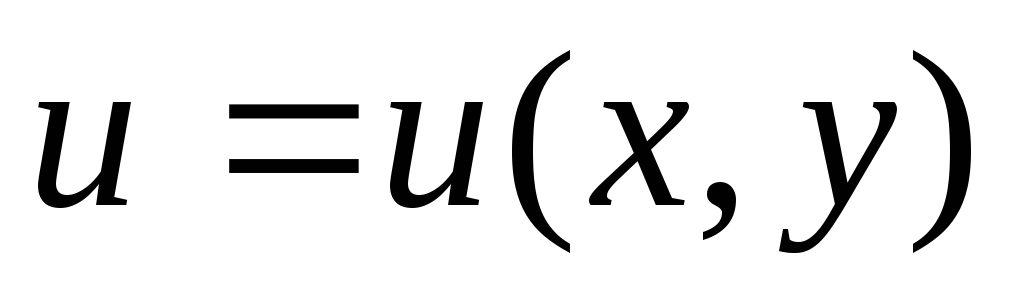по ее полному дифференциалу.

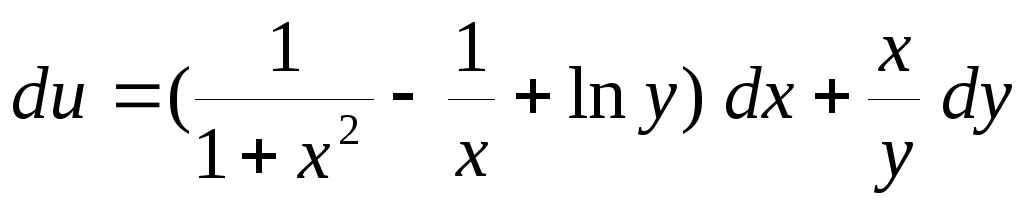12. Вычислить поверхностный интеграл первого рода 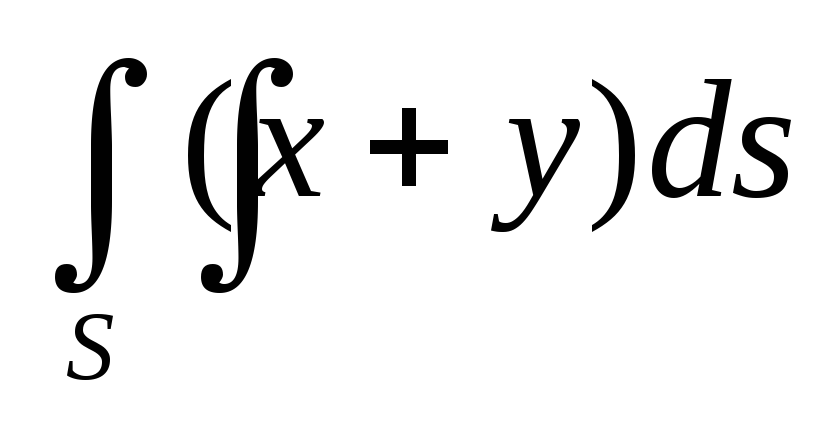по пространственной области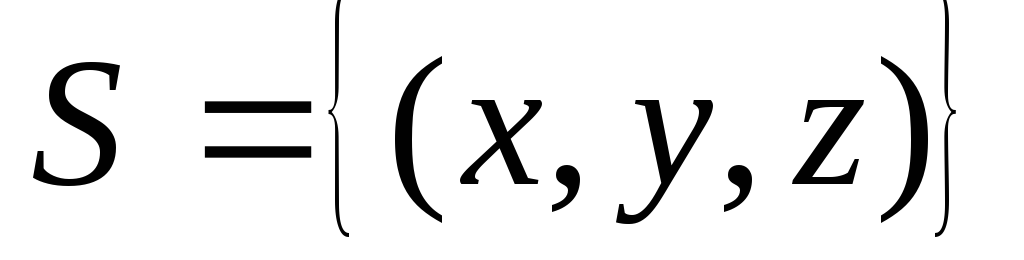, определяемой условиями.

13. Вычислить поверхностный интеграл второго рода гдеS– внешняя сторона поверхности верхней полусферы.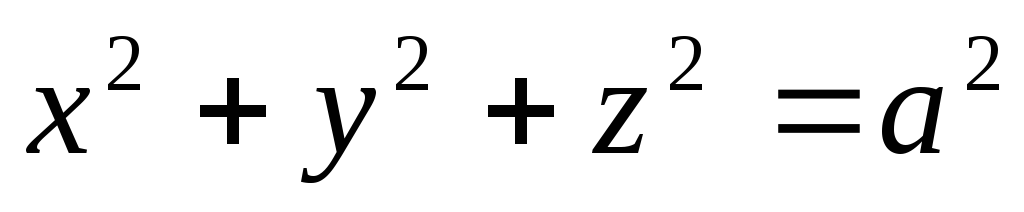

Вариант 14

1. Изменить порядок интегрирования .

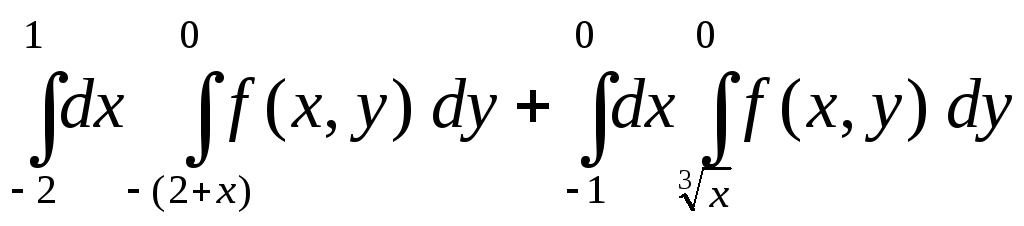2. Вычислить двойной интеграл по квадратуD:.

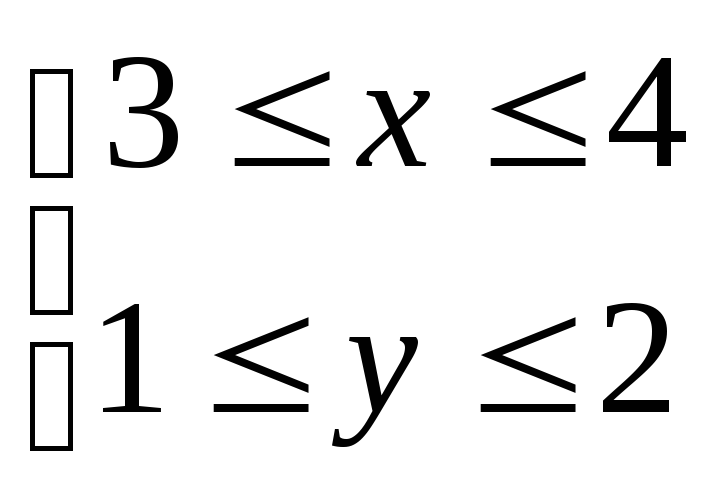3. Вычислить площадь плоской пластины D, определяемой уравнением:.

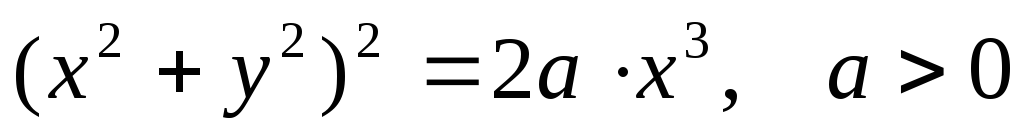4. Вычислить объем тела V, ограниченного поверхностями. Плотность телаVсчитать равной единице.

5. Вычислить тройной интеграл по пространственной областиV, ограниченной поверхностями.

6. Вычислить тройной интеграл 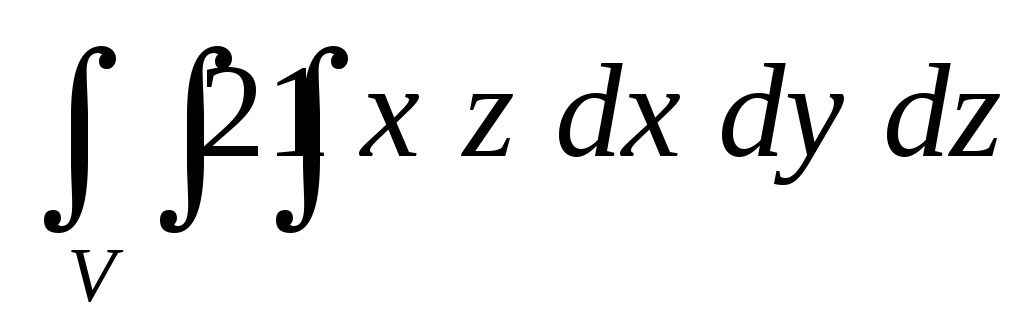, если областьVограничена поверхностями.

7. Найти центр тяжести однородного полушара .

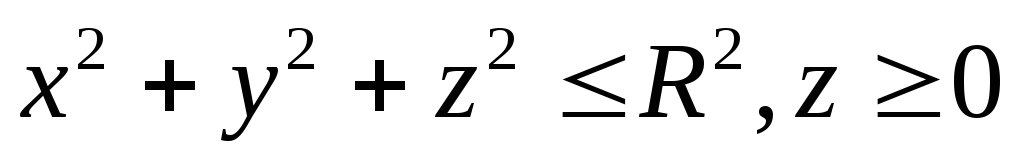8. Вычислить криволинейный интеграл первого рода , еслиL– дуга параболы.

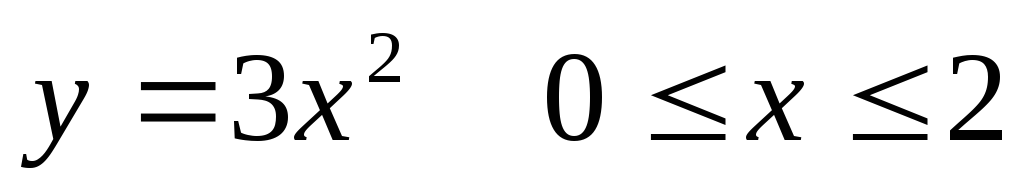9. Определить центр тяжести дуги астроиды 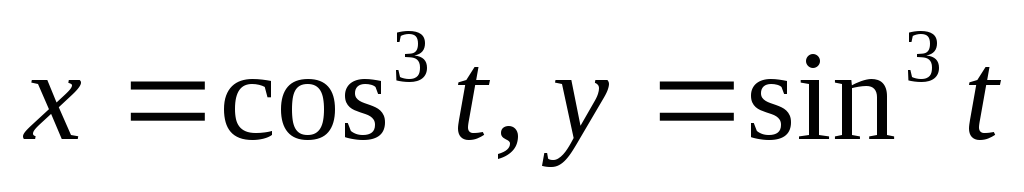, лежащей во второй четверти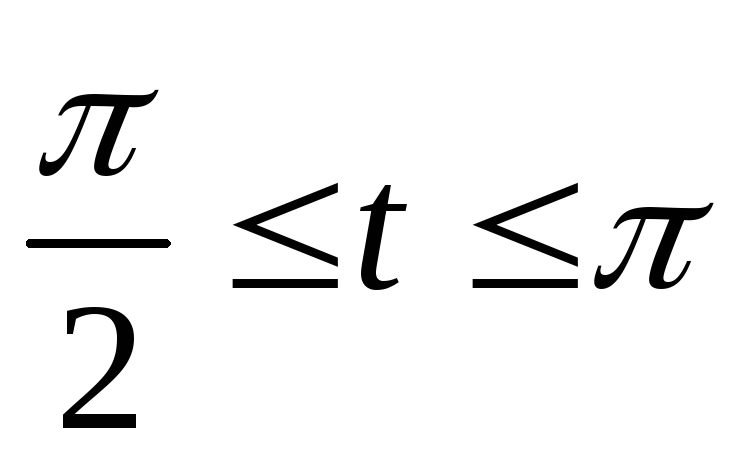, плотность считать равной 2.

10. Вычислить криволинейный интеграл второго рода , гдеL- отрезок прямой от точки А(0,0) до точки В.

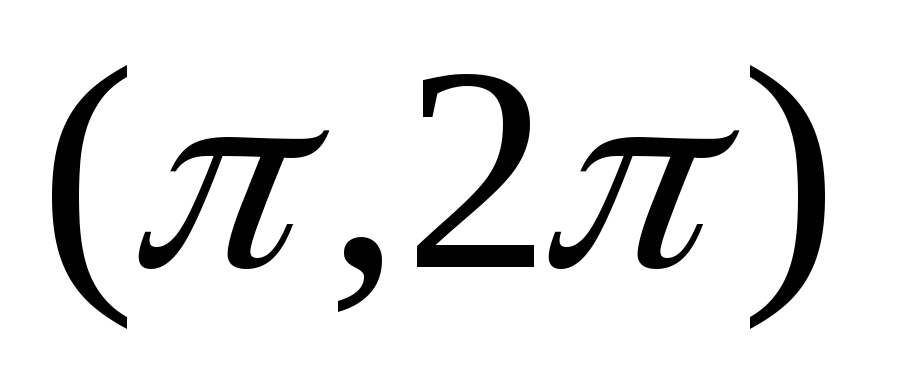11. Вычислить площадь, ограниченную эллипсом .

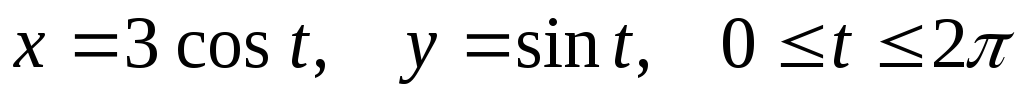12. Вычислить поверхностный интеграл первого рода 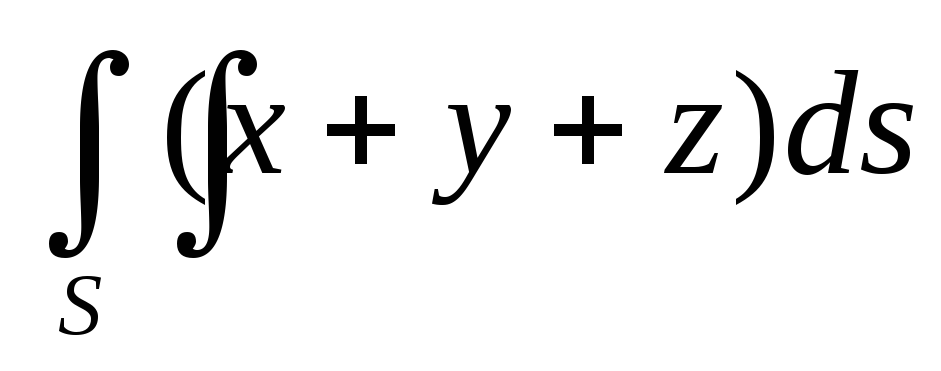по пространственной области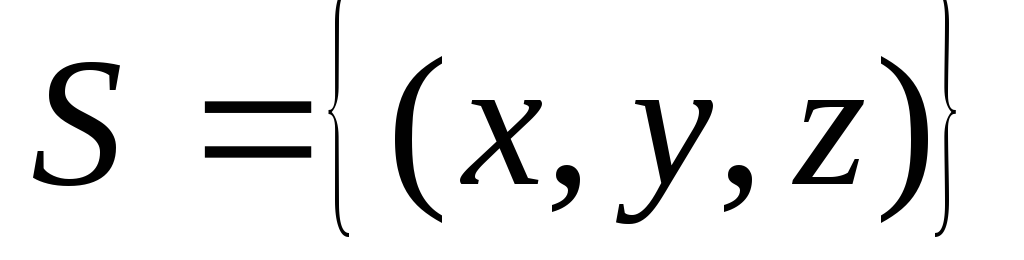, определяемой условиями.

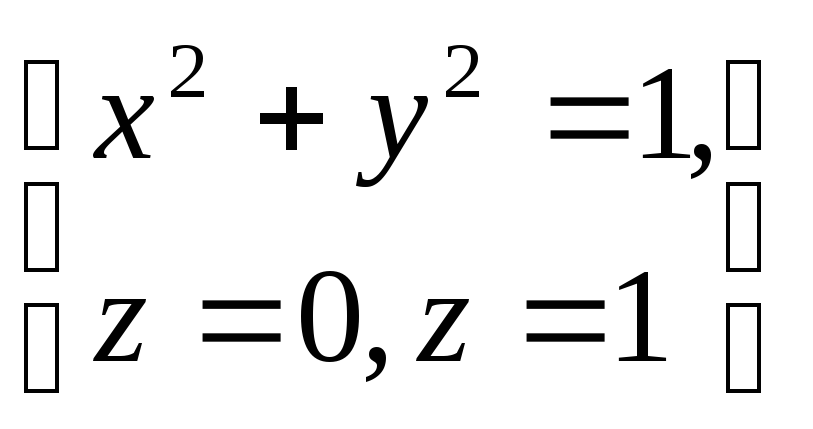13. Вычислить поверхностный интеграл второго рода 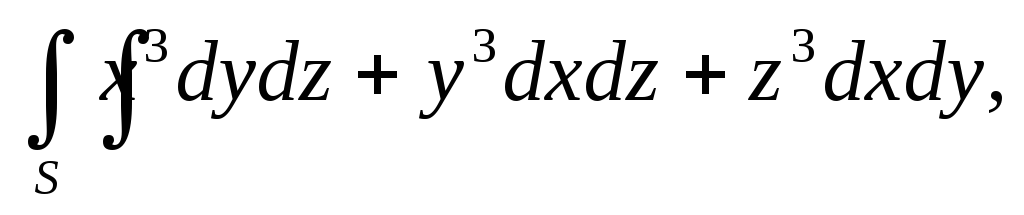гдеS– внешняя сторона поверхности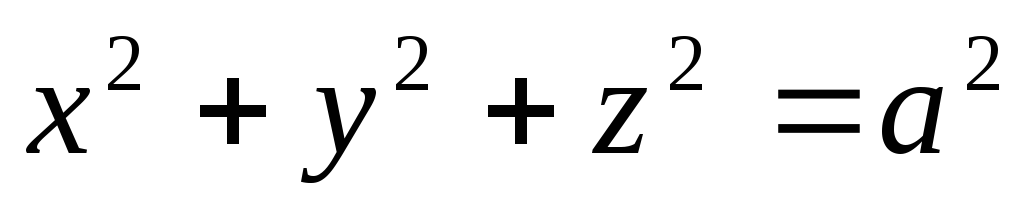.