Вариант 9

1. Изменить порядок интегрирования в повторном интеграле .

2. Вычислить двойной интеграл 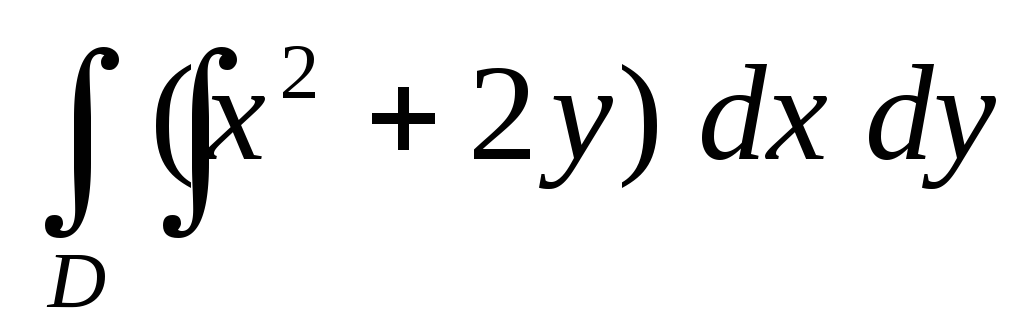по квадратуD:.

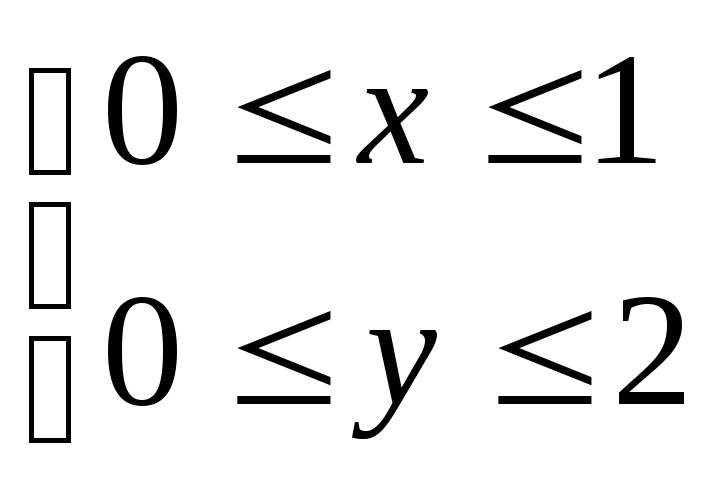3. Вычислить массу плоской пластины D, определяемой условиями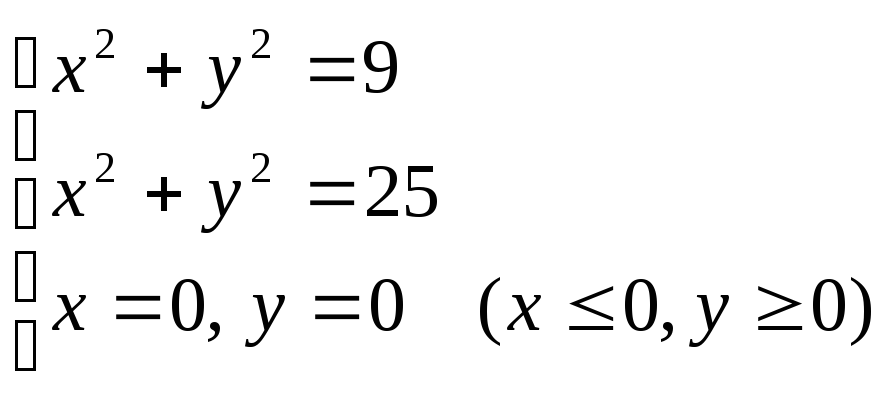с распределенной на ней плотностью.

4. Вычислить объем тела V, ограниченного поверхностями. Плотность телаVсчитать равной единице.

5. Вычислить тройной интеграл 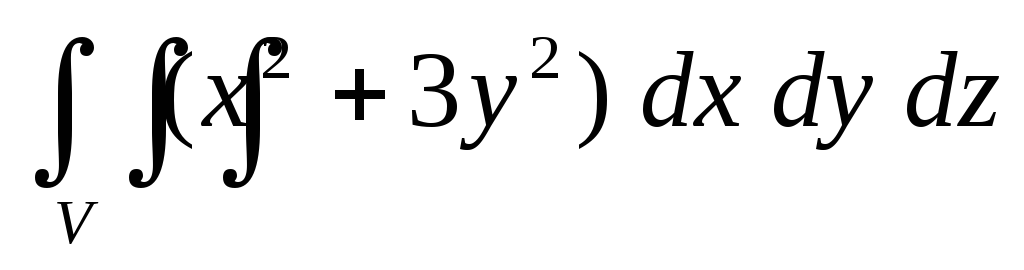по пространственной областиV, ограниченной плоскостями.

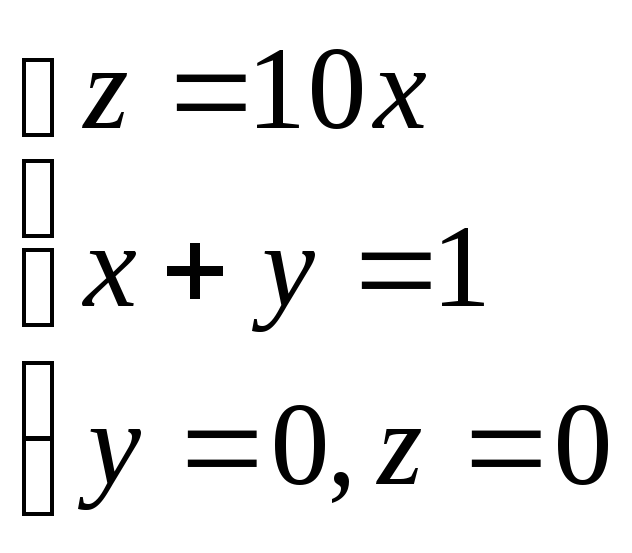6. Вычислить интеграл .

7. Найти весь объем, заключенный между конусом 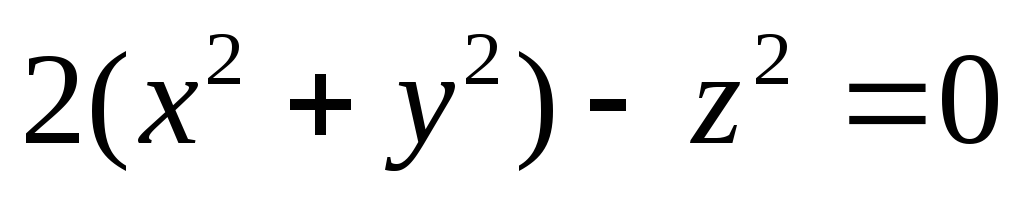и гиперболоидом.

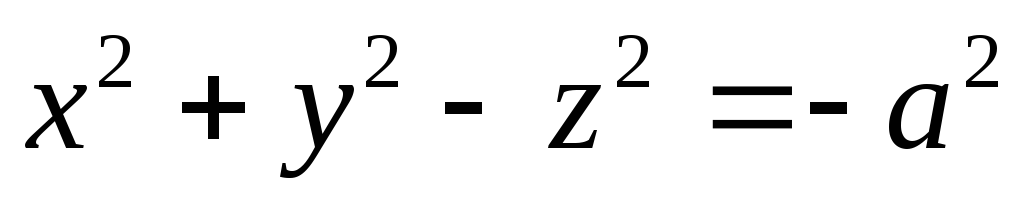8. Вычислить криволинейный интеграл первого рода 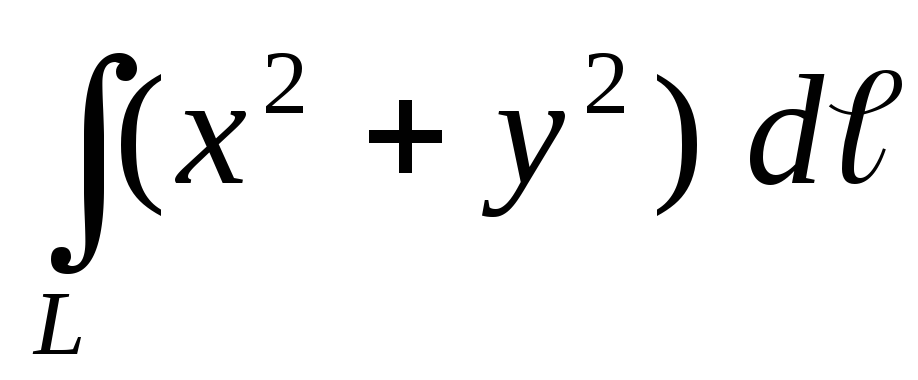по дуге циклоидыL:.

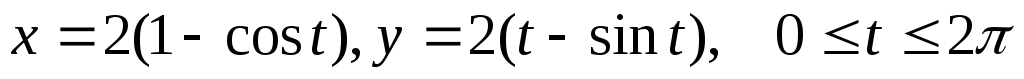9. Найти массу дуги линии 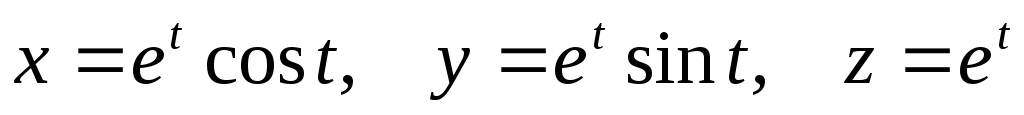от точки, соответствующей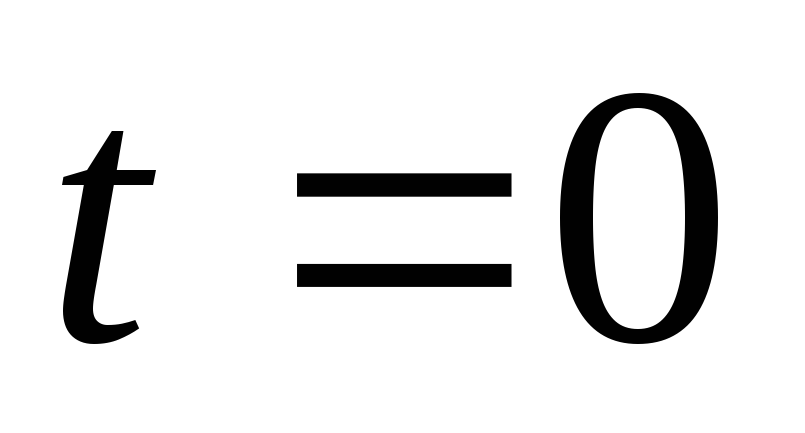до произвольной точки, если плотность дуги обратно пропорциональна квадрату полярного радиуса и в точке (1,0,1) равна единице.

10. Вычислить криволинейный интеграл второго рода 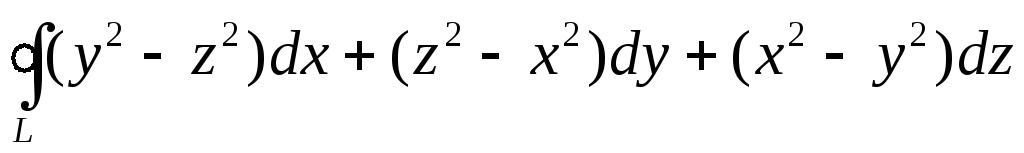, гдеL– контур, образованный линиями пересечения сферы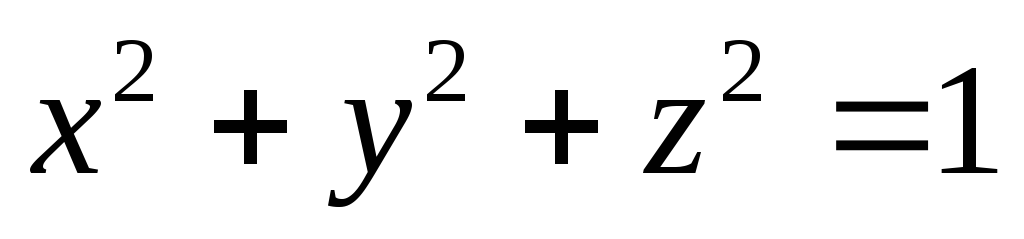с координатными плоскостями,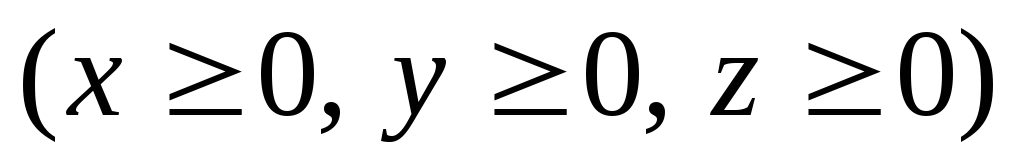при положительном направлении обхода.

11. Убедившись, что подынтегральное выражение является полным дифференциалом, вычислить криволинейный интеграл 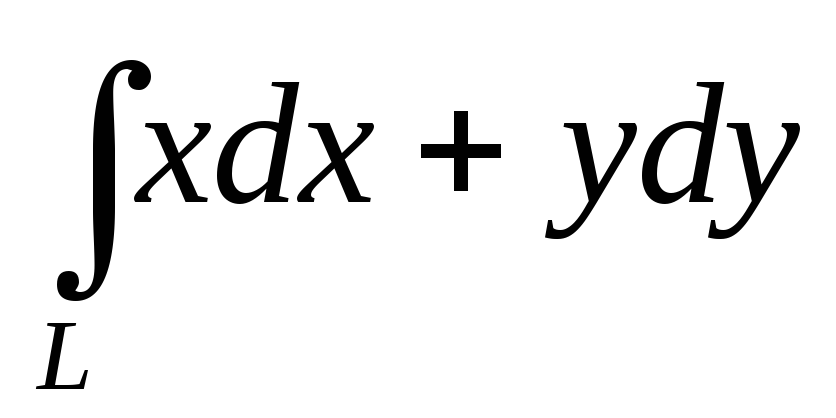по кривойLс началом в точке А(1,1) и концом в точке В(2,2).

12. Вычислить поверхностный интеграл первого рода 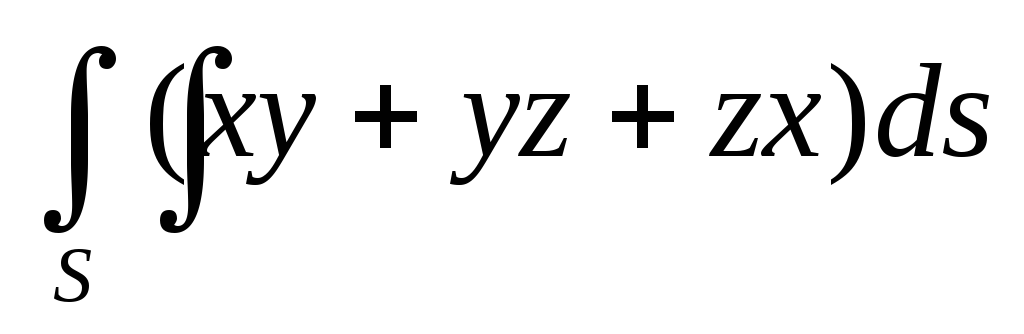по пространственной области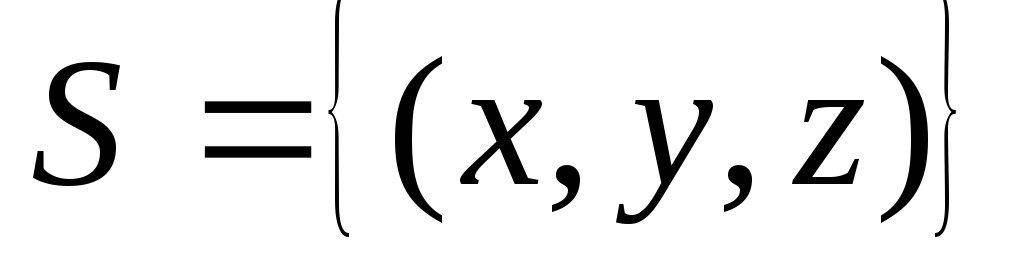, определяемой условиями.

13. Вычислить поверхностный интеграл IIродапо верхней стороне верхней половины сферы.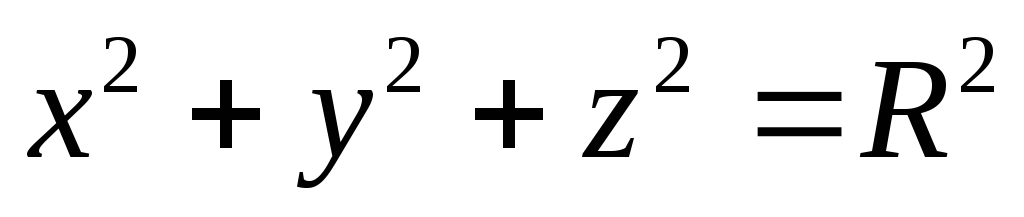

Вариант 10

1. Изменить порядок интегрирования в повторном интеграле .

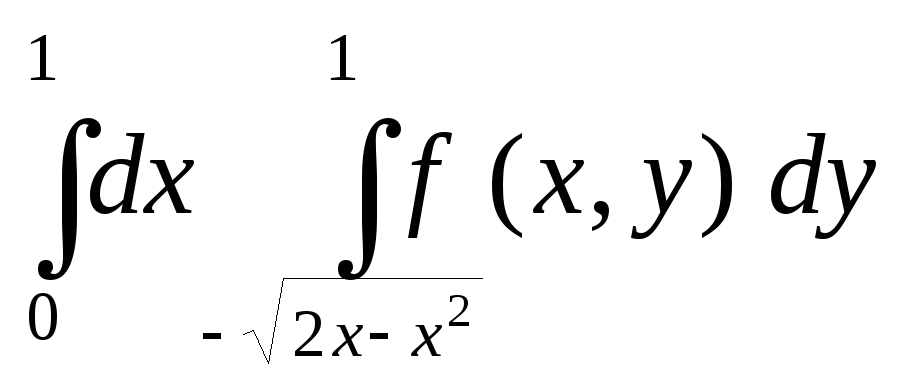2. Вычислить двойной интеграл по областиD, ограниченной линиями.

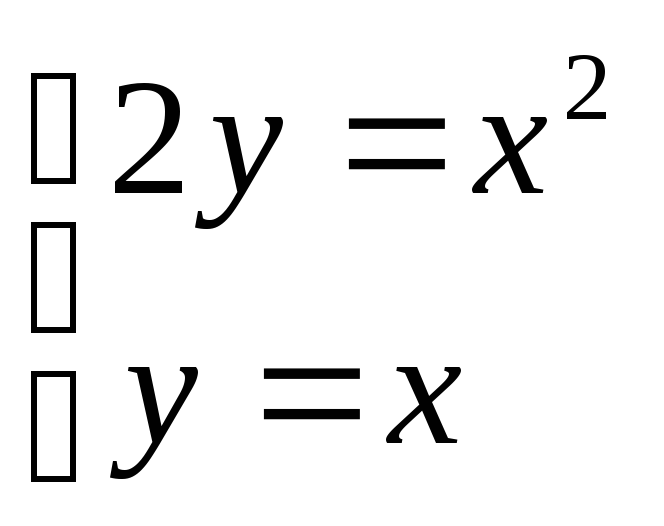3. Вычислить площадь плоской пластины D, определяемой уравнениями.

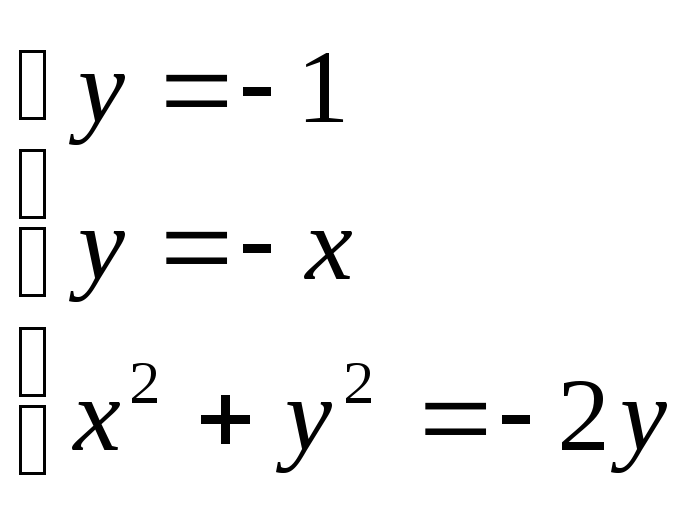4. Вычислить объем тела V, ограниченного поверхностями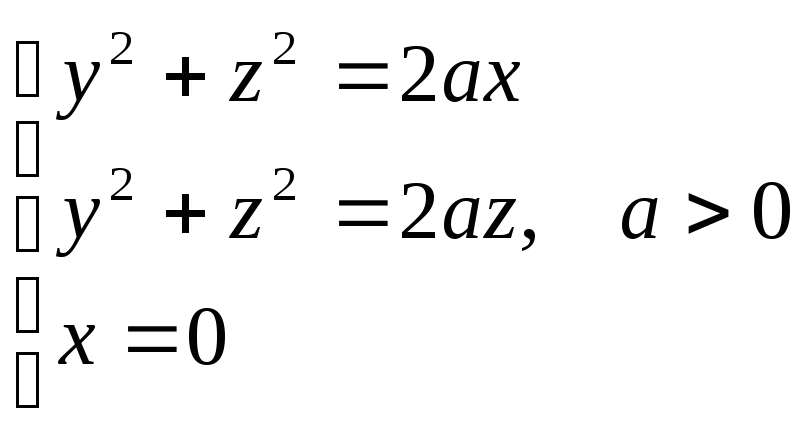. Плотность телаVсчитать равной единице.

5. Вычислить тройной интеграл 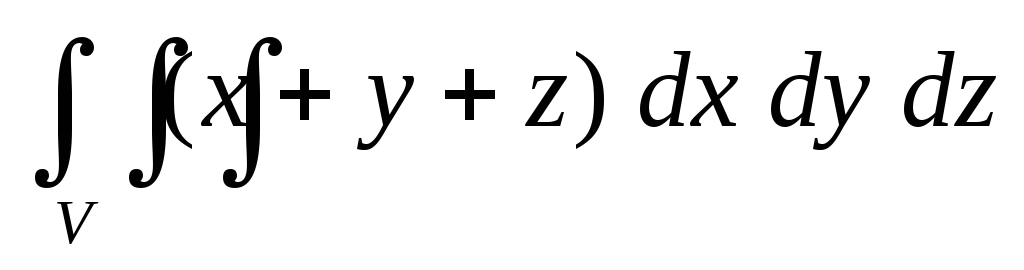по пространственной областиV, ограниченной плоскостями.

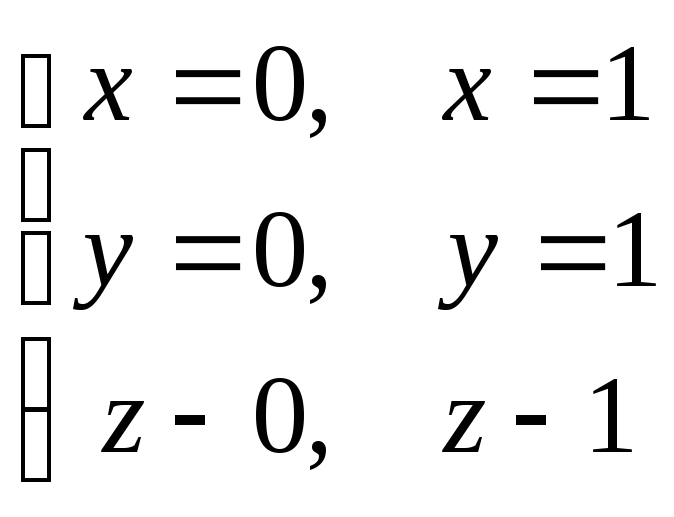6. Вычислить тройной интеграл 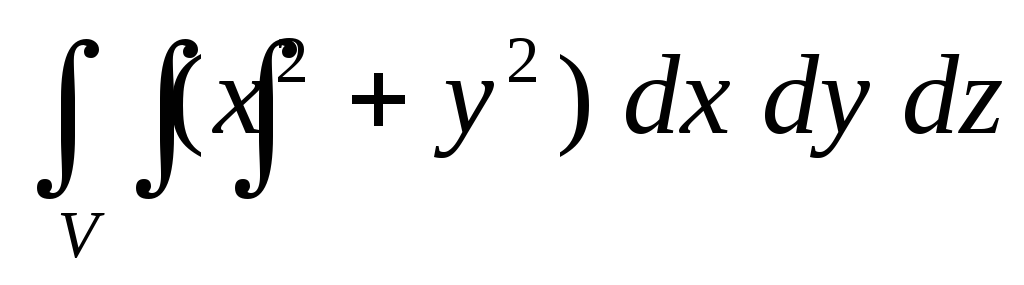, если областьVограничена поверхностями .

7. Вычислить массу тела, ограниченного поверхностямии имеющего массу.

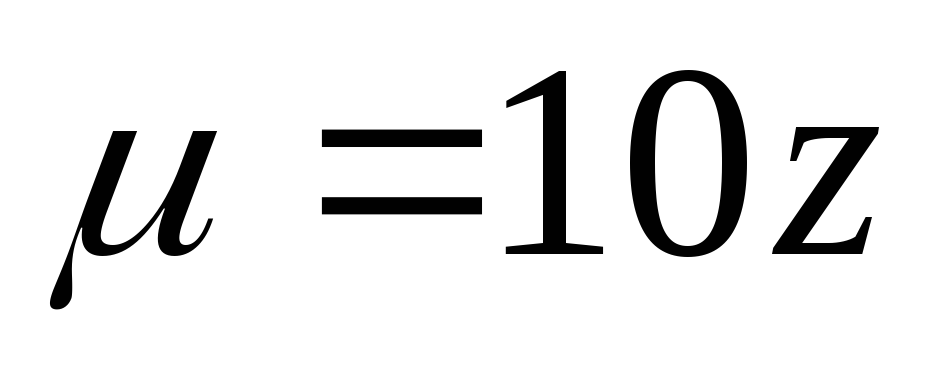8. Вычислить криволинейный интеграл первого рода 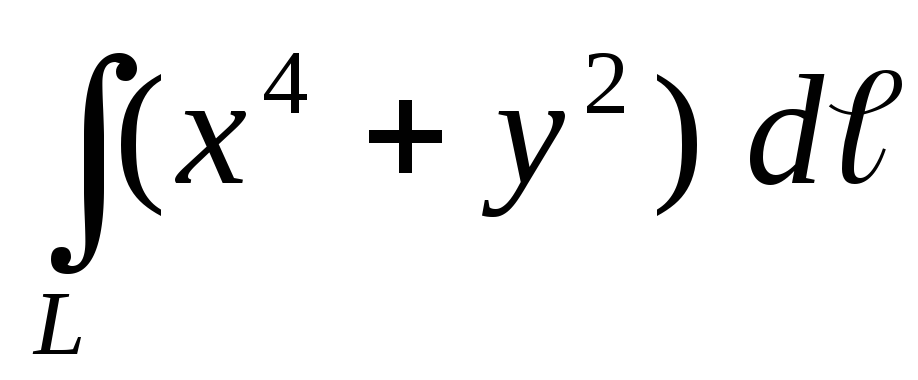по кривойL:.

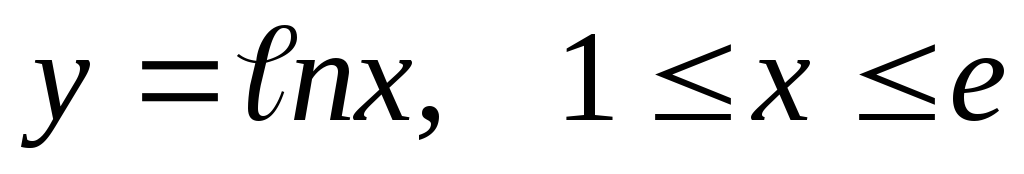9. Найти координаты центра масс первого полувитка винтовой линии 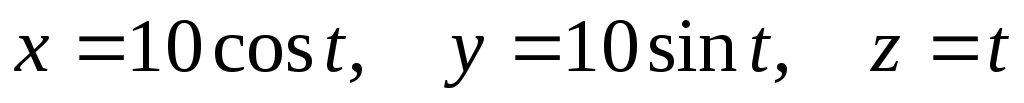, считая плотность постоянной

10. Вычислить криволинейный интеграл второго рода , гдеL– дуга окружности радиуса 2 с центром в начале координат при положительном направлении обхода.

11. Вычислить площадь, ограниченную эллипсом .

12. Вычислить поверхностный интеграл первого рода 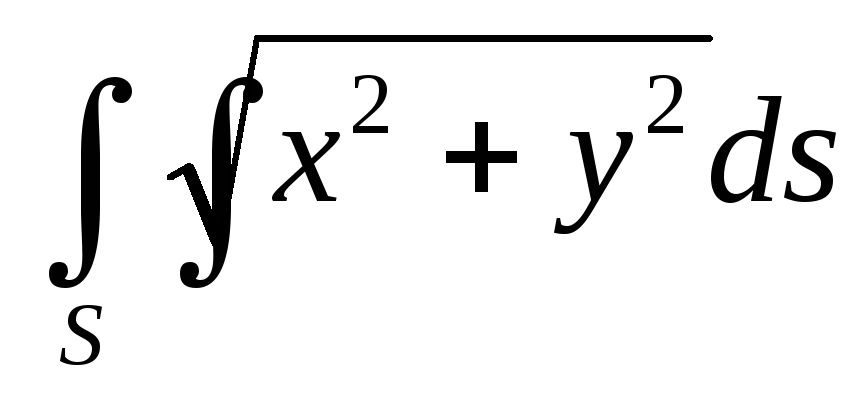по пространственной области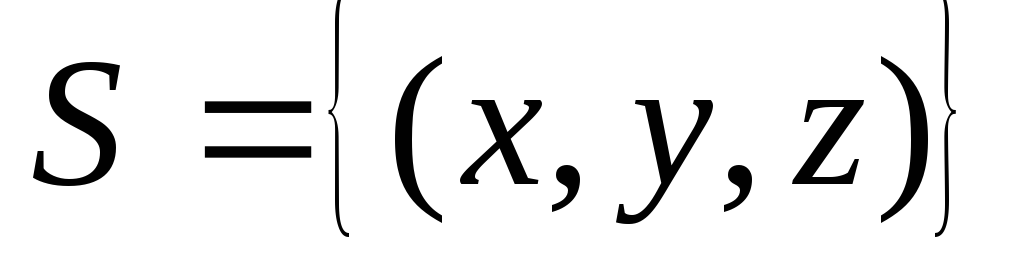, определяемой условиями.

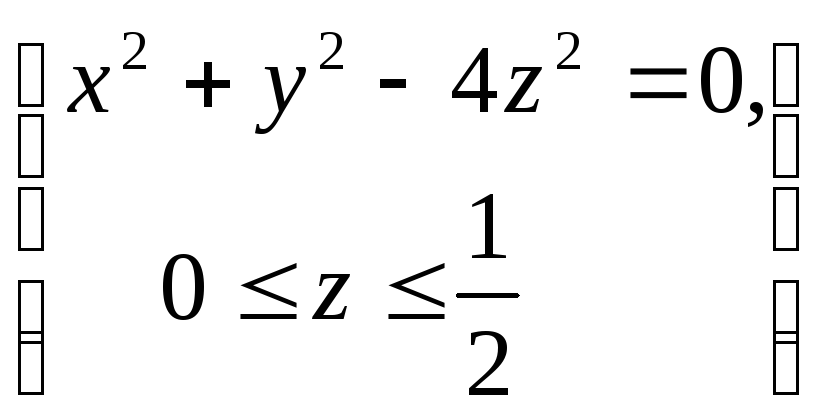13. Вычислить поверхностный интеграл второго рода 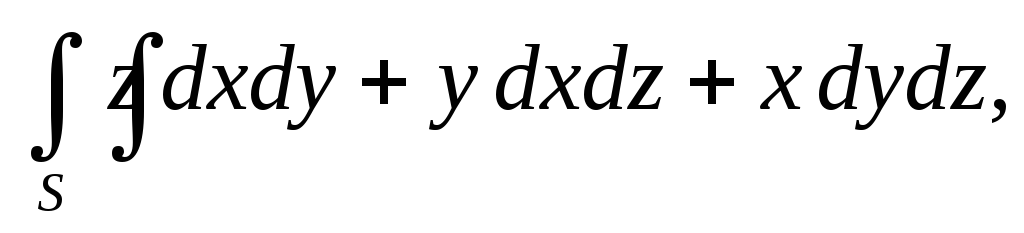гдеS– верхняя сторона плоскости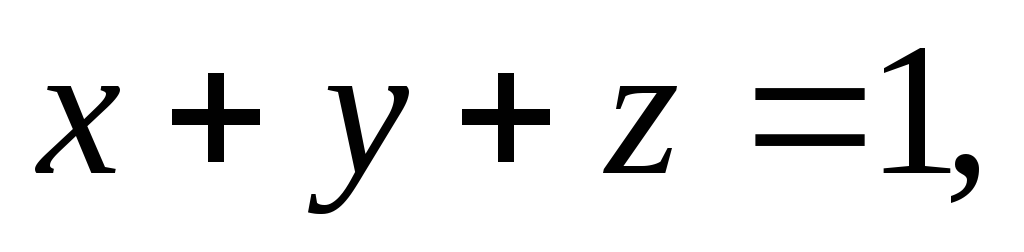ограниченной координатными плоскостями.

Вариант 11

1. Изменить порядок интегрирования в повторном интеграле .

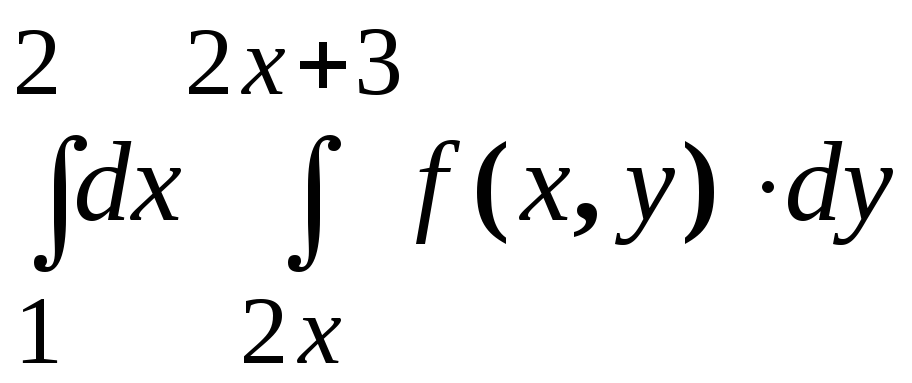2. Вычислить двойной интеграл по областиD, ограниченной прямыми.

3. Вычислить площадь плоской пластины D, определяемой уравнением.

4. Вычислить объем тела V, ограниченного поверхностями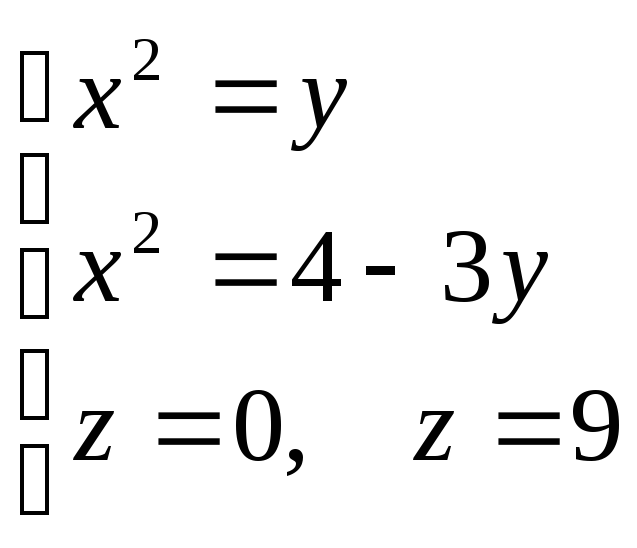. Плотность телаVсчитать равной единице.

5. Вычислить тройной интеграл 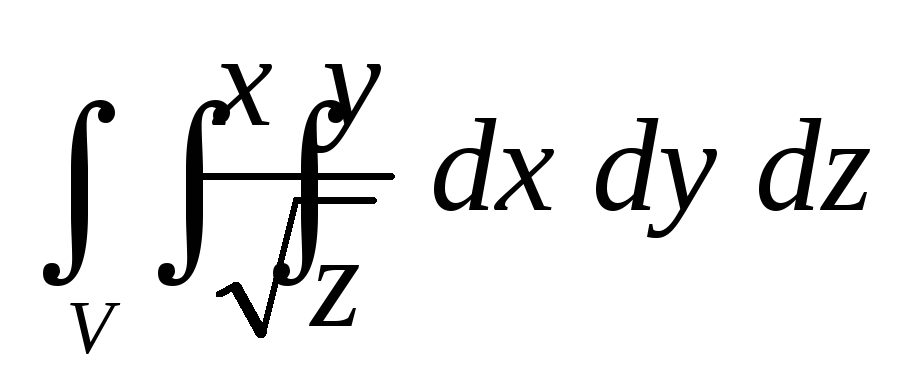по пространственной областиV, ограниченной поверхностями.

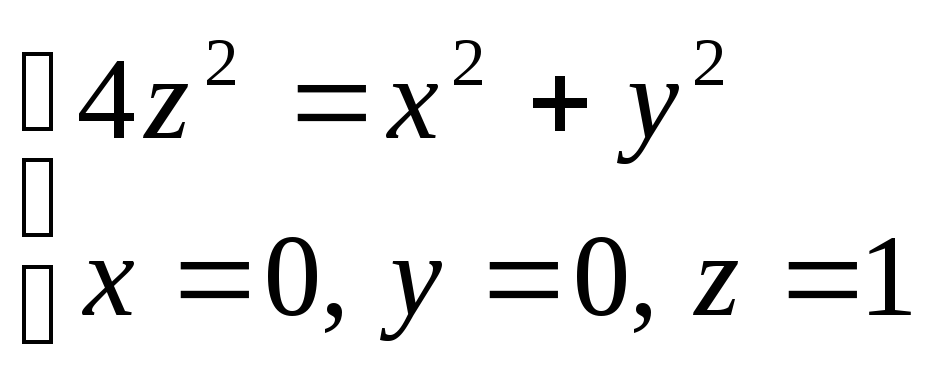6. Вычислить интеграл .

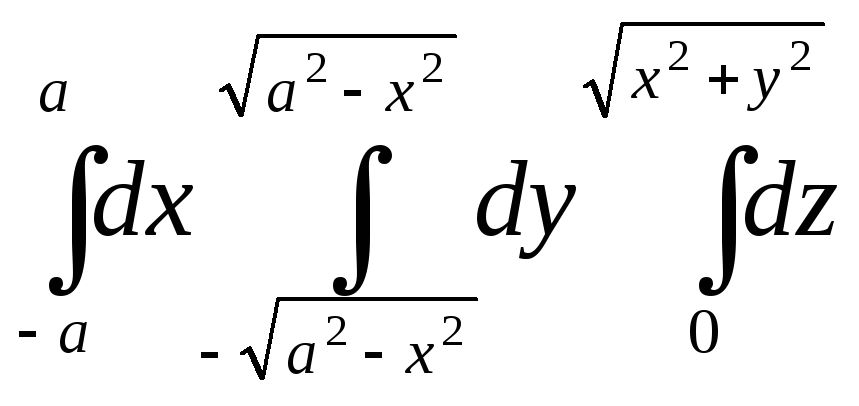7. Найти объем тела, ограниченного параболоидам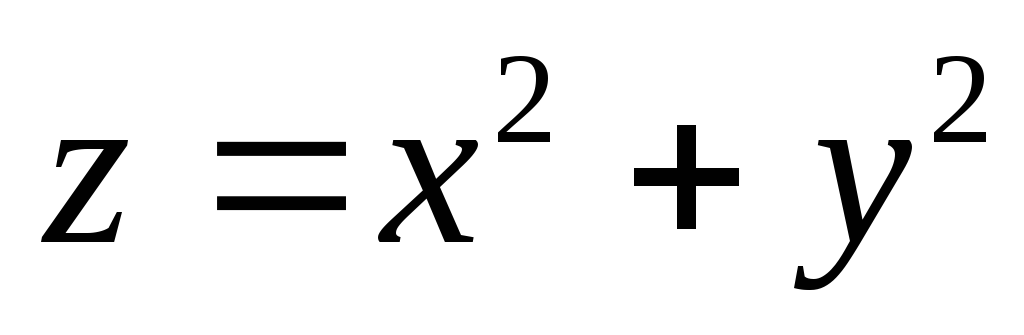и ии плоскостями.

8. Вычислить криволинейный интеграл первого рода 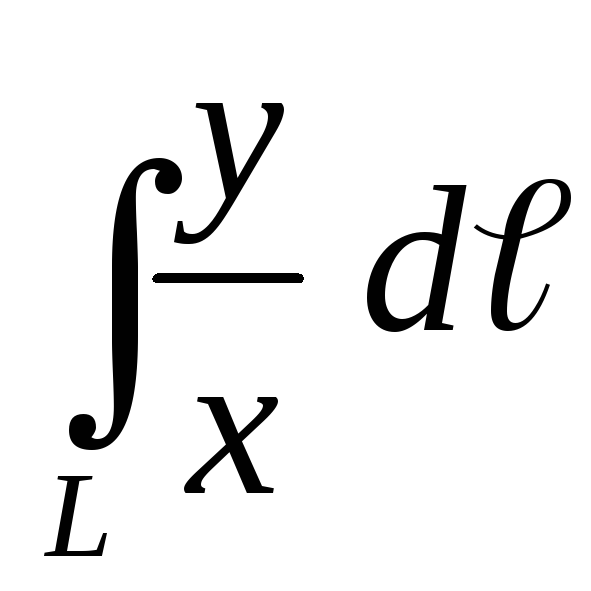по кривойL:.

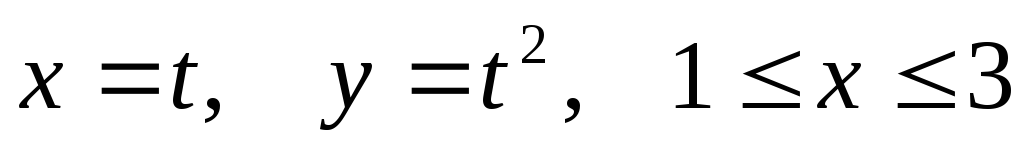9. Вычислить статический момент первого витка винтовой линии 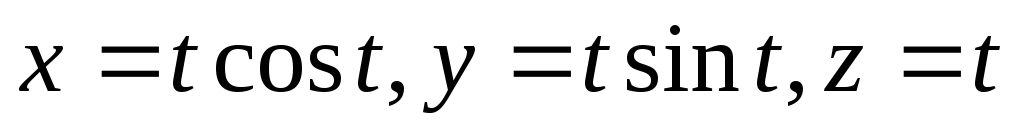, относительно плоскости Оxy, считая плотность пропорциональной квадрату расстояния от этой плоскости.

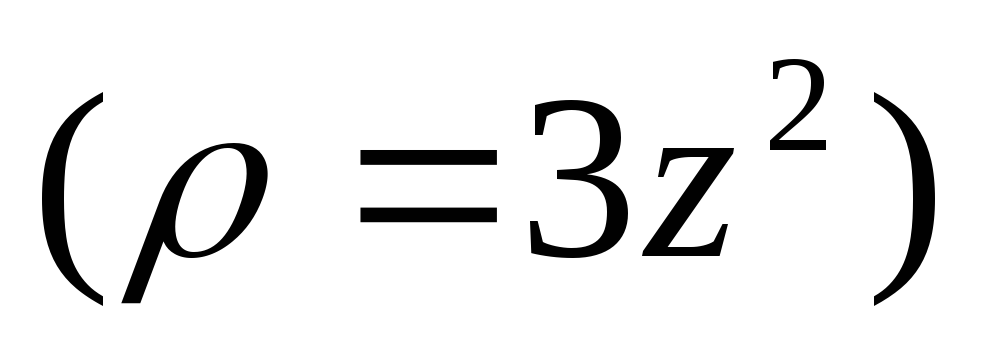10. Вычислить криволинейный интеграл второго рода 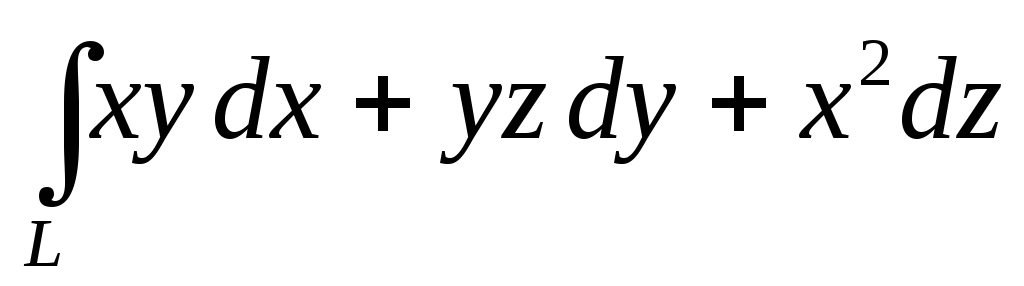, гдеL– дуга винтовой линии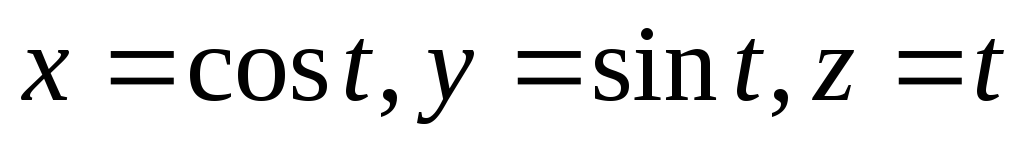от точки А (1,0,0) до точки В (1,0,2).

11. Найти работу, совершаемую при перемещении материальной точки вдоль дуги Lот точки А(0,0) до точки В(1,1) силой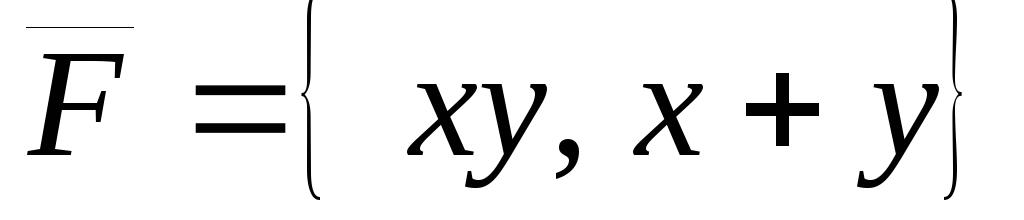в случае, еслиL– отрезок прямой и в случае, еслиL– дуга параболы.

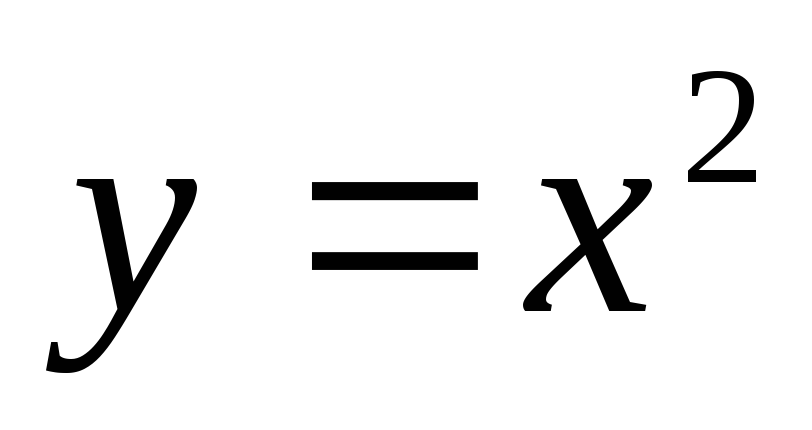12. Вычислить поверхностный интеграл первого рода по пространственной области, определяемой условиями.

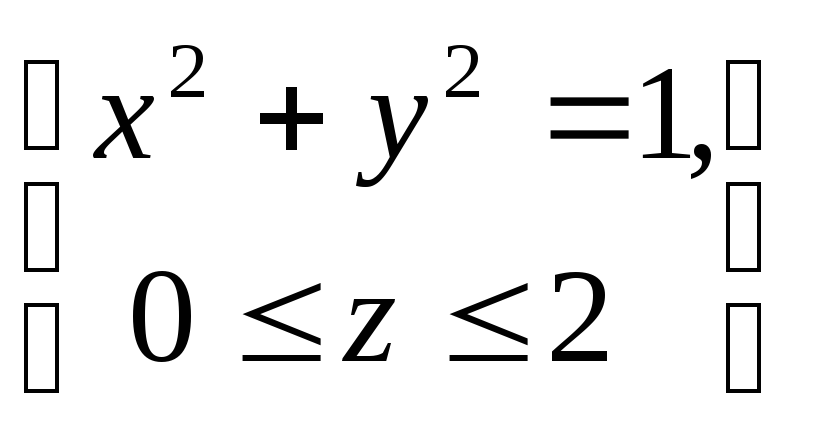13. Вычислить поверхностный интеграл второго рода 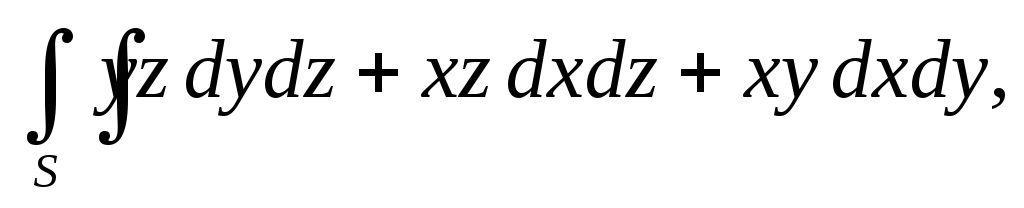гдеS– внешняя сторона поверхности, ограниченной плоскостями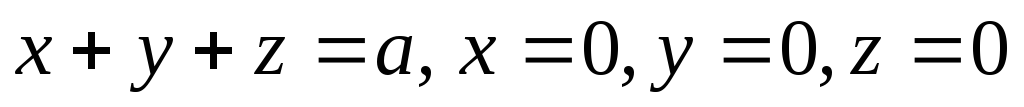.