Вариант 6

1. Изменить порядок интегрирования .

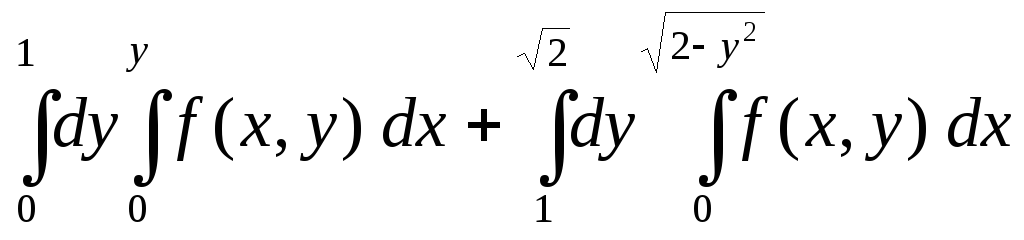2. Вычислить двойной интеграл по областиD, ограниченной линиями.

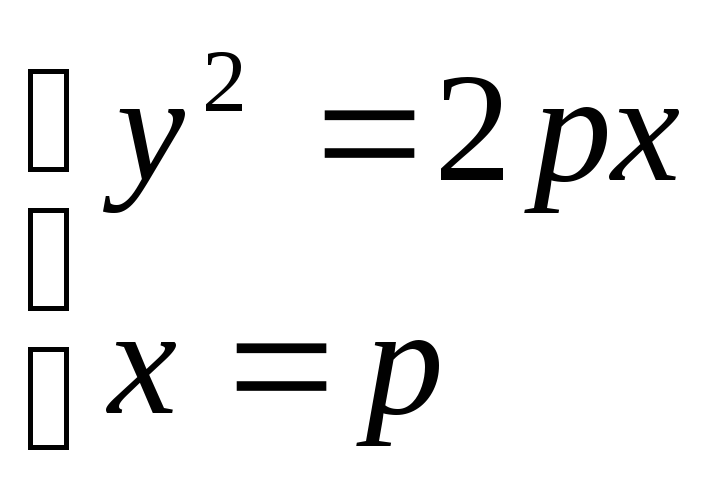3. Вычислить площадь плоской пластины D, определяемой уравнениями.

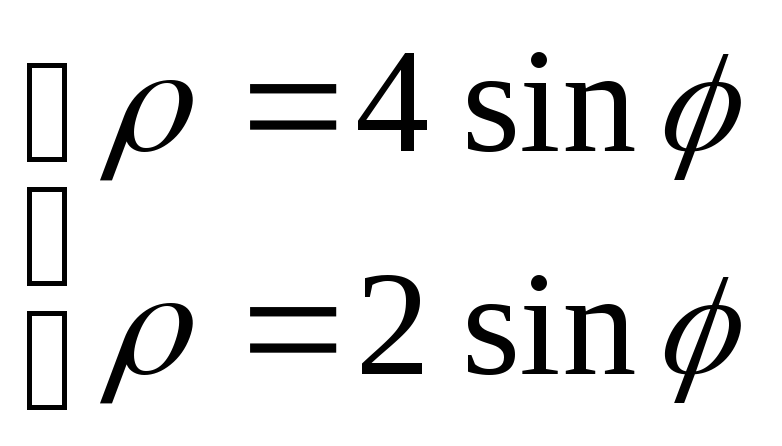4. Вычислить объем тела V, ограниченного поверхностями. Плотность телаVсчитать равной единице.

5. Вычислить тройной интеграл 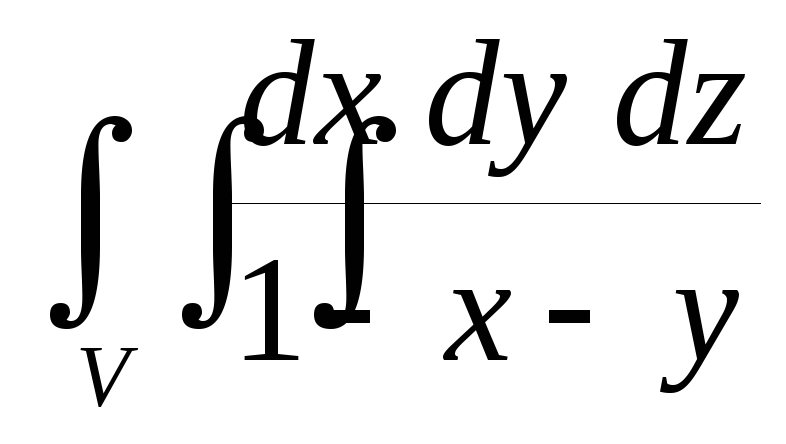по пространственной областиV, определяемой уравнениями.

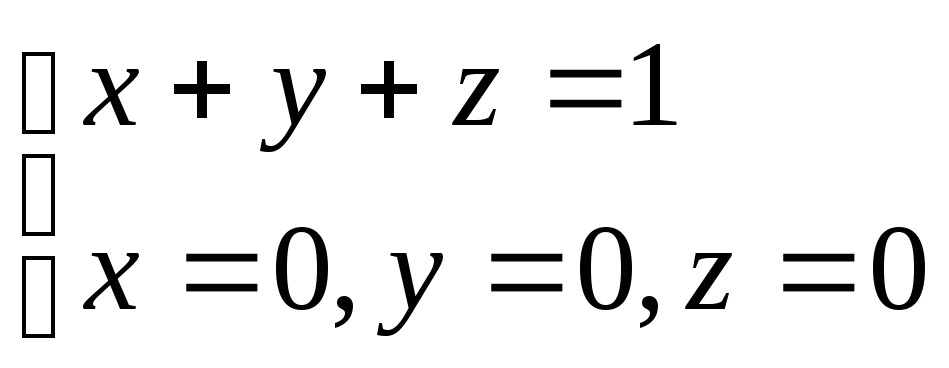6. Вычислить интеграл , если областьVопределена условиями.

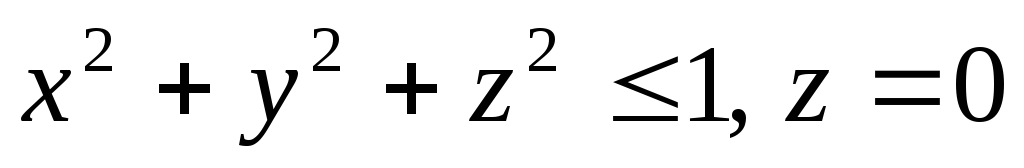7. Найти объем тела, ограниченного параболоидом 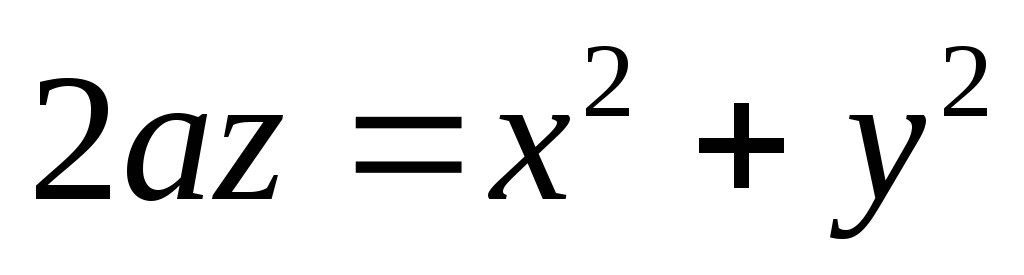и шаром.

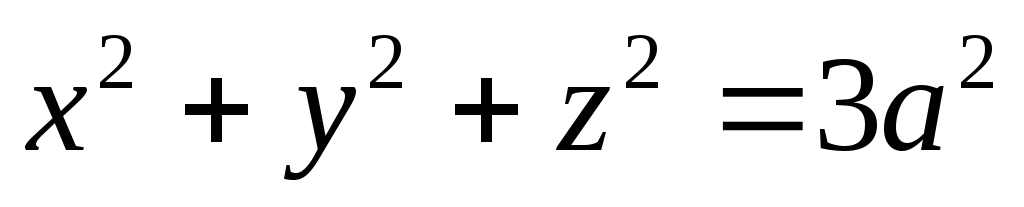8. Вычислить криволинейный интеграл первого рода 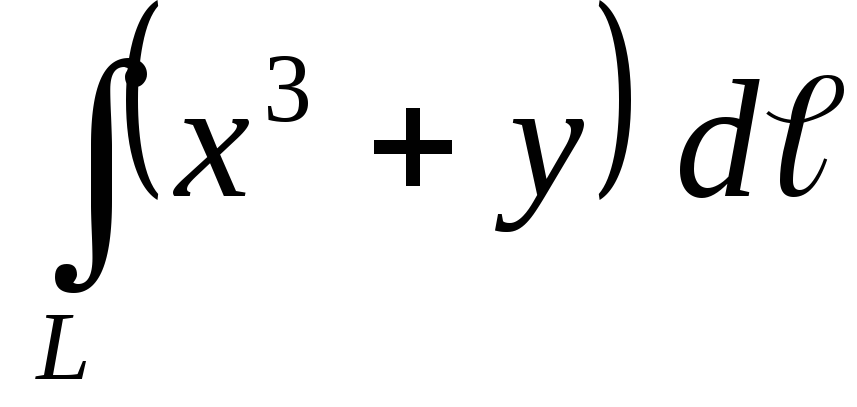по кривойL:.

9. Найти массу кривой 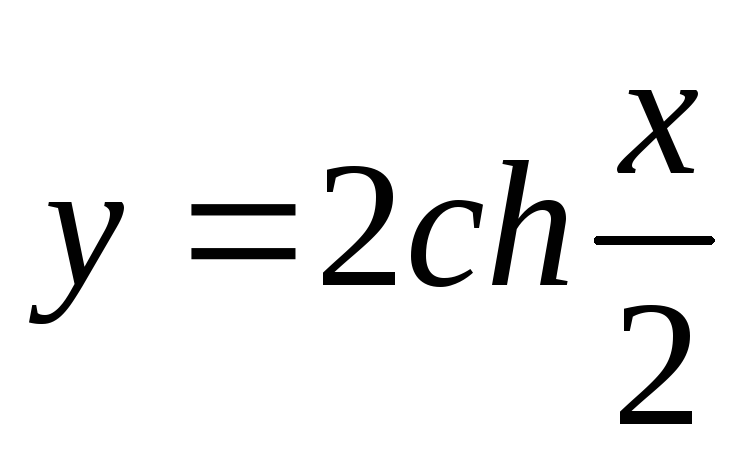на участке от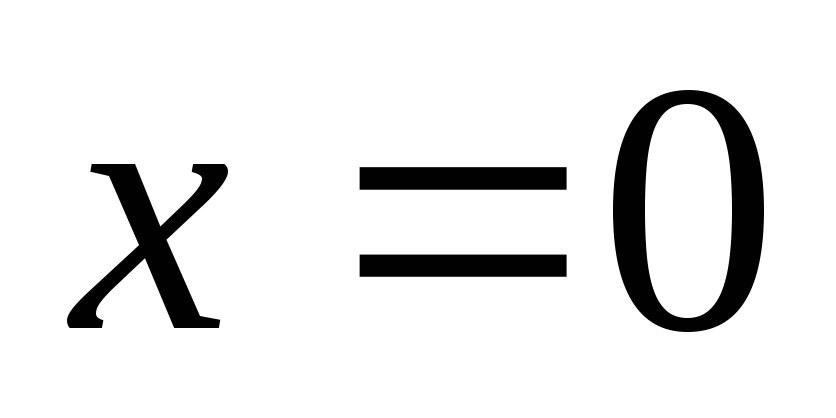досчитая, что в каждой точке плотность обратно пропорциональна ординате этой точки.

10. Вычислить криволинейный интеграл второго рода 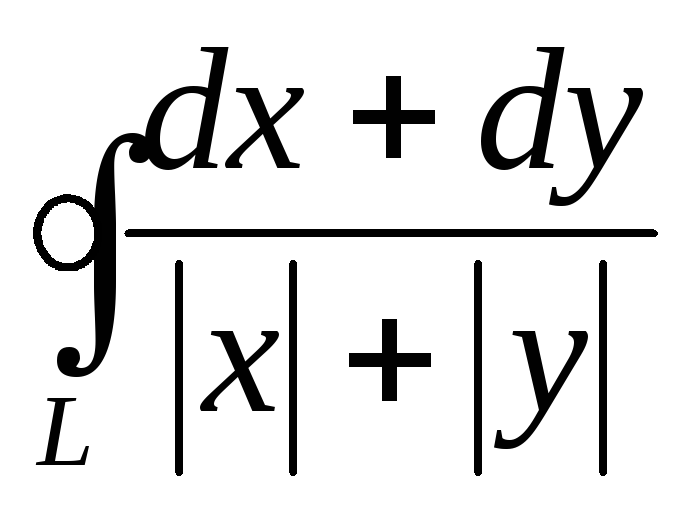,L-контур квадрата АВСDс вершинами А(1,0), В(0,1), С(-1,0),D(0,-1), взятый при положительном направлении обхода.

11. Найти работу, совершаемую силой 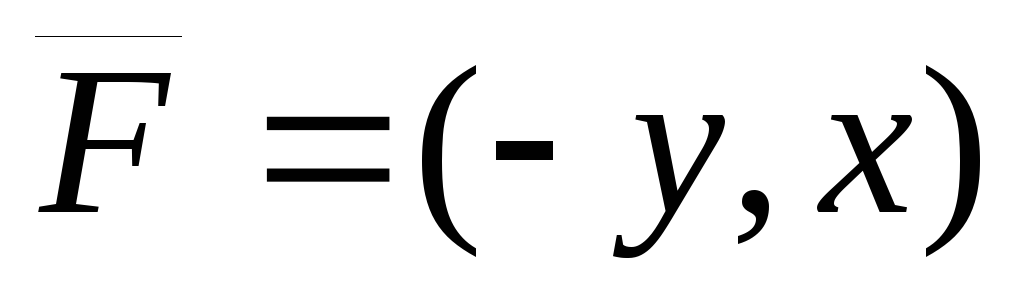при перемещении материальной точки вдоль верхней полуокружностив положительном направлении.

12. Вычислить поверхностный интеграл первого рода 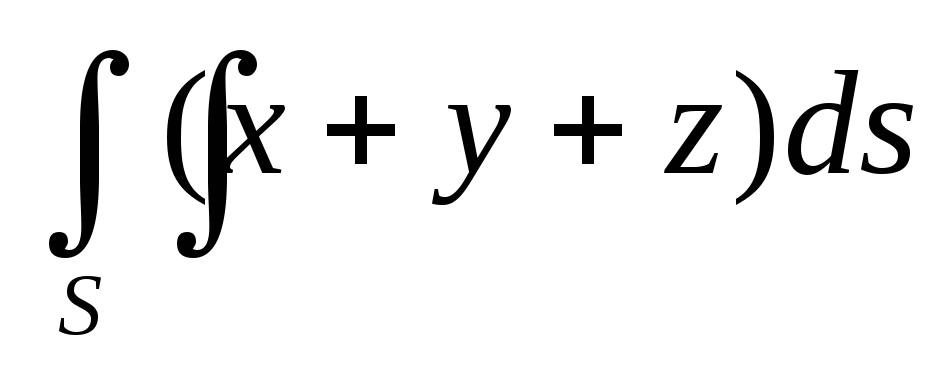по пространственной области, определяемой условиями.

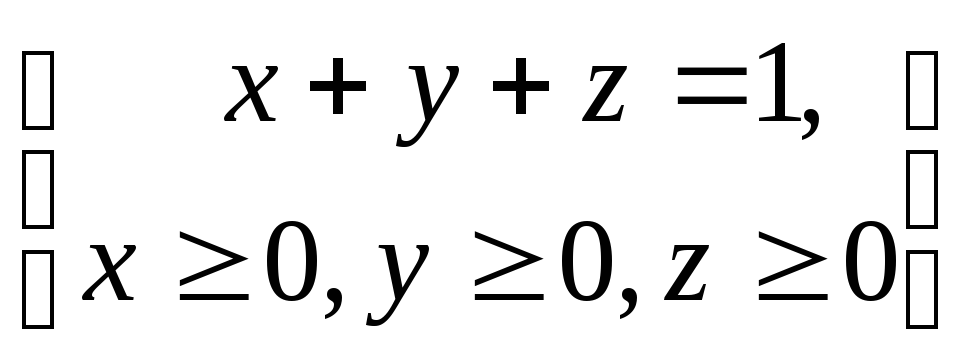13. С помощью формулы Остроградского-Гаусса вычислить поверхностный интеграл IIрода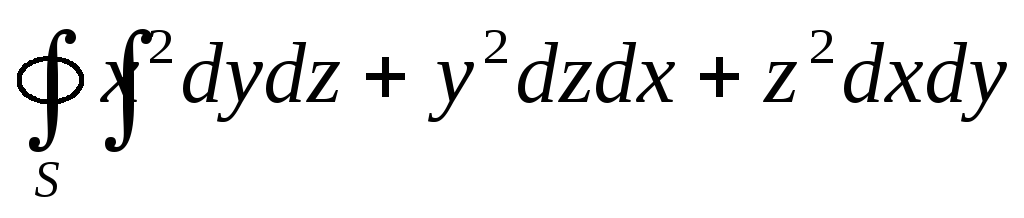по внешней сторонеSсферы.

Вариант 7

1. Изменить порядок интегрирования .

2. Вычислить двойной интеграл 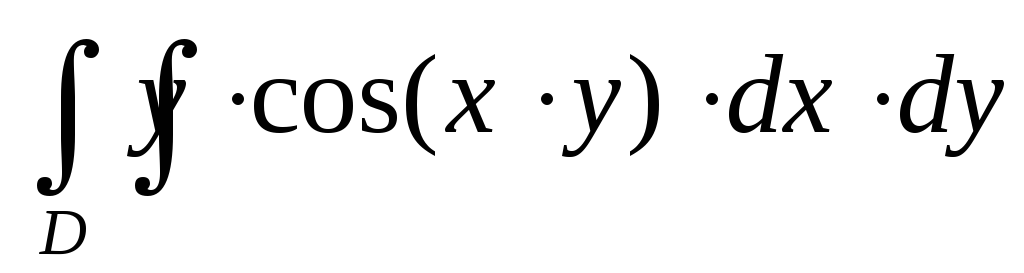по областиD, ограниченной линиями.

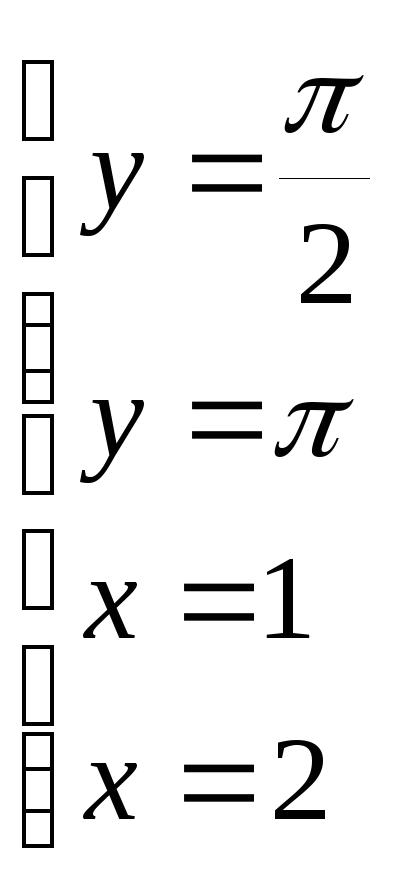3. Вычислить площадь плоской пластины D, определяемой уравнениями.

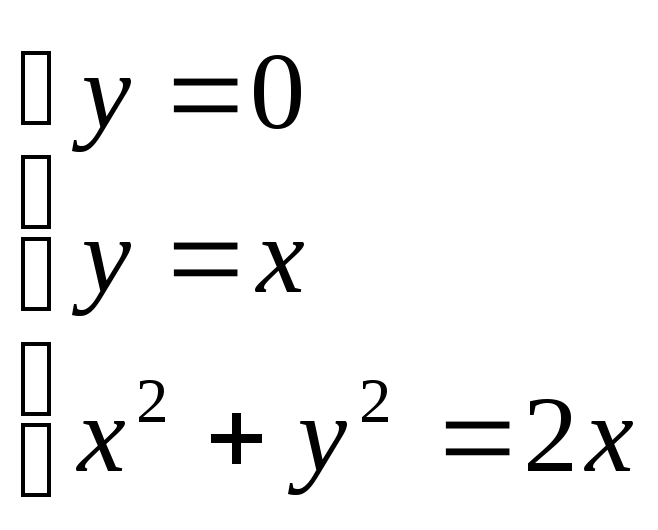4. Вычислить объем тела V, ограниченного поверхностями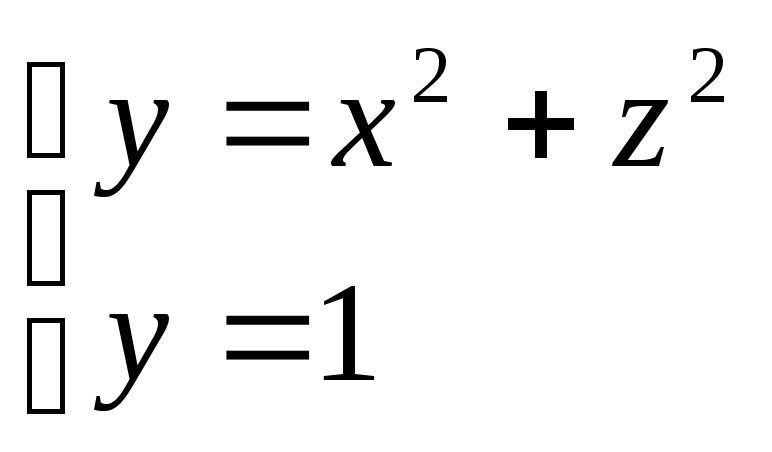. Плотность телаVсчитать равной единице.

5. Вычислить тройной интеграл 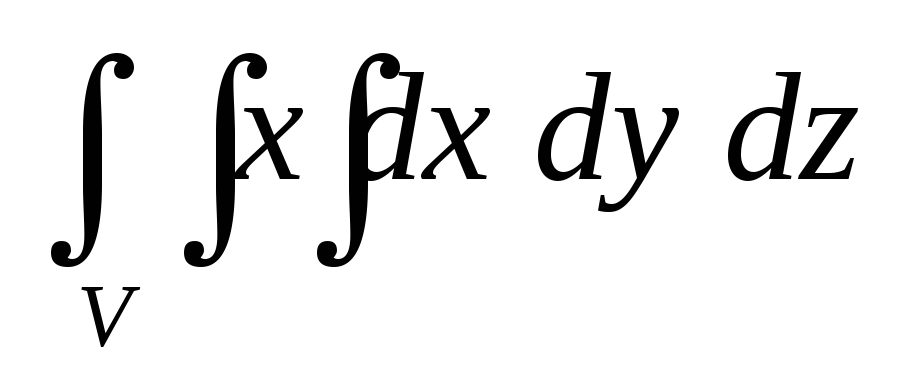по пространственной областиV, определяемой уравнениями.

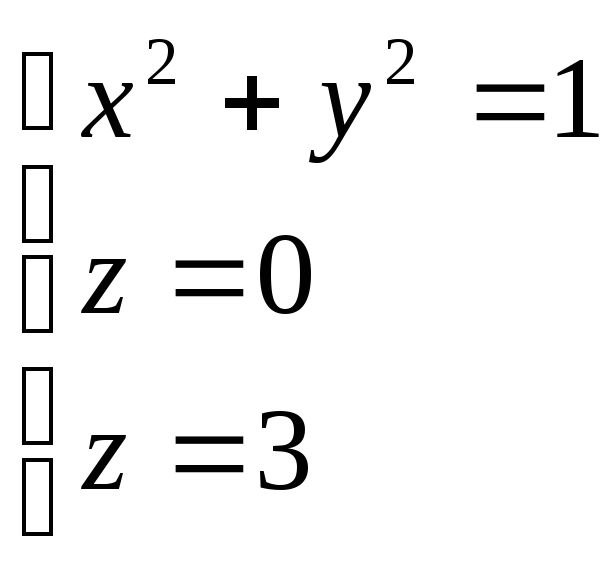6. Вычислить интеграл 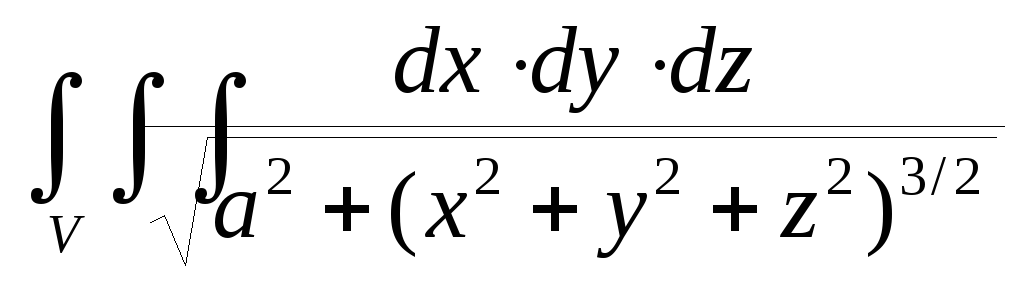, если областьVопределена условием.

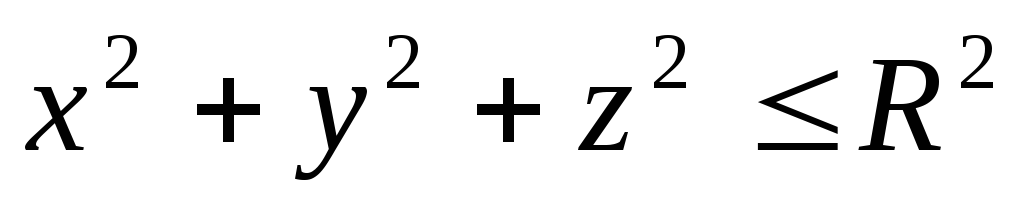7. Вычислить координаты центра масс и моменты инерции пирамиды, ограниченной плоскостями .

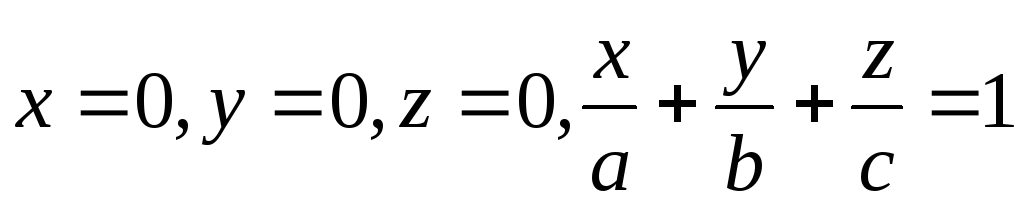8. Вычислить криволинейный интеграл первого рода 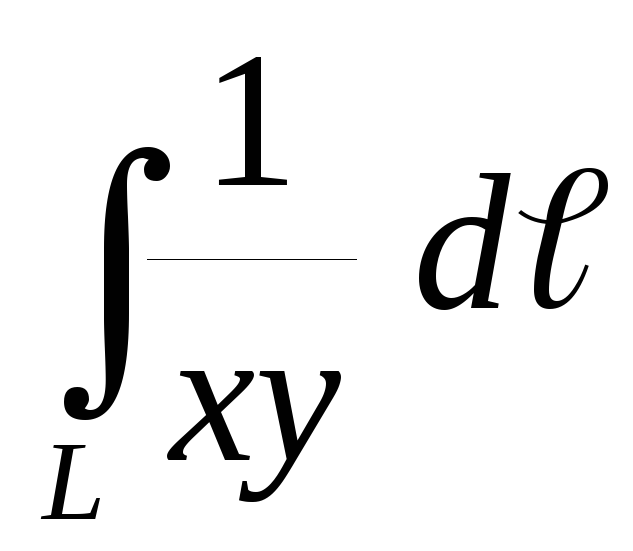по дуге астроидыL:.

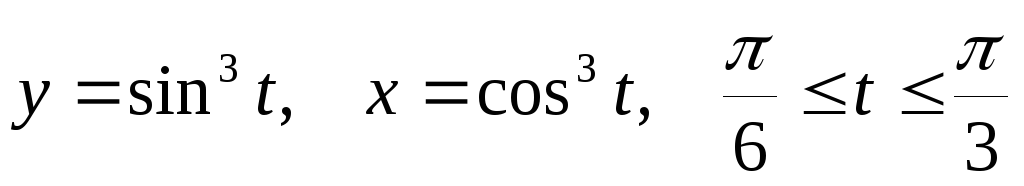9. Вычислить массу эллипса L, определенного параметрическими уравнениями.

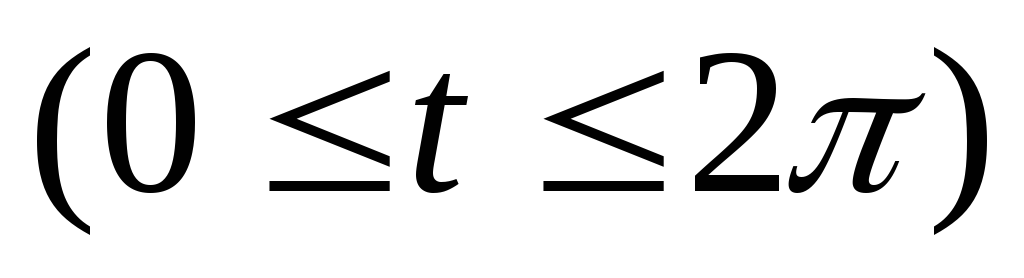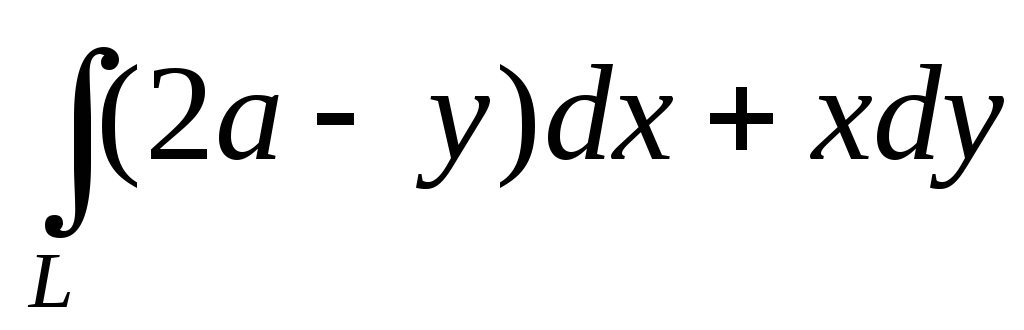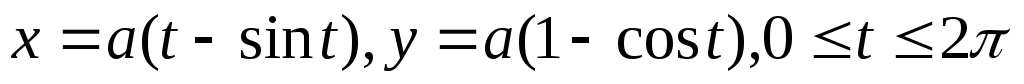10. Вычислить криволинейный интеграл второго рода , гдеL– арка циклоидыпри положительном направлении обхода.

11. Найти работу силы , совершаемую при перемещении материальной точки вдоль окружности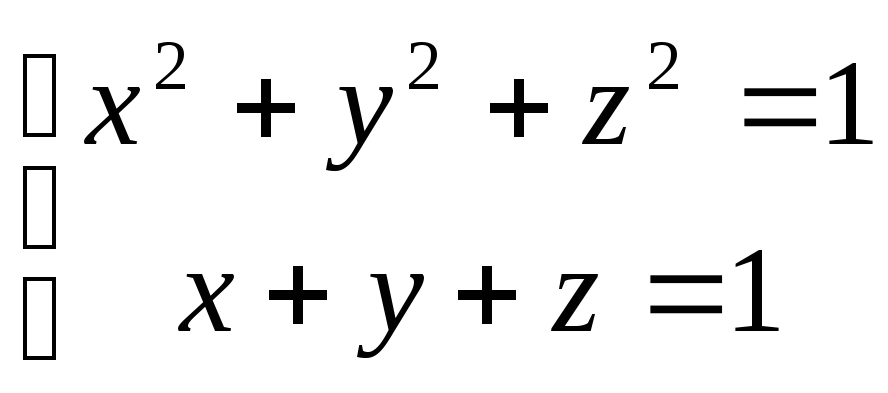, ориентированной против часовой стрелки со стороны осиOz.

12. Вычислить поверхностный интеграл первого рода 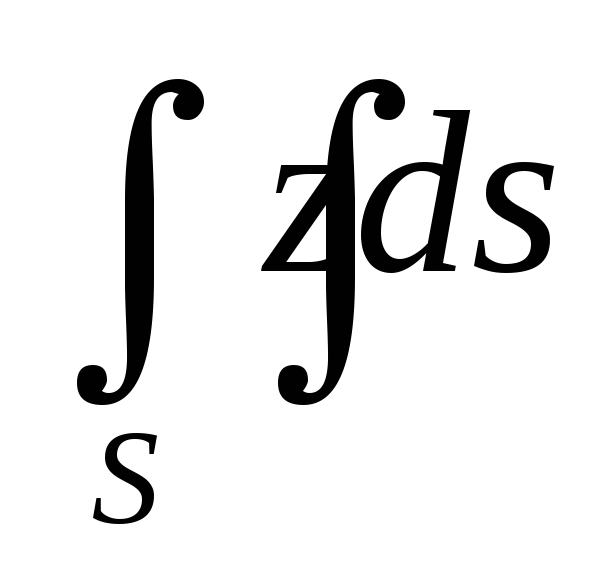по пространственной области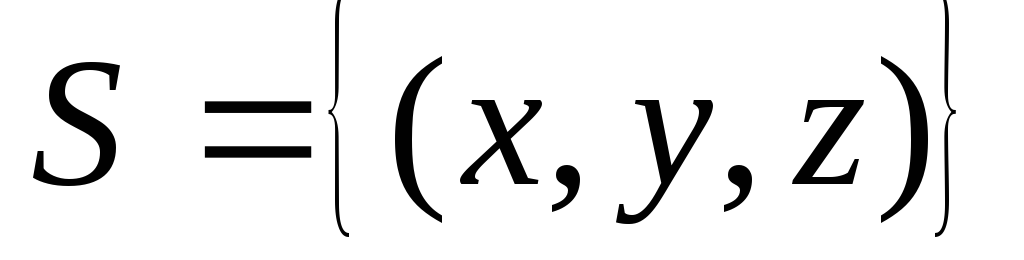, определяемой условиями.

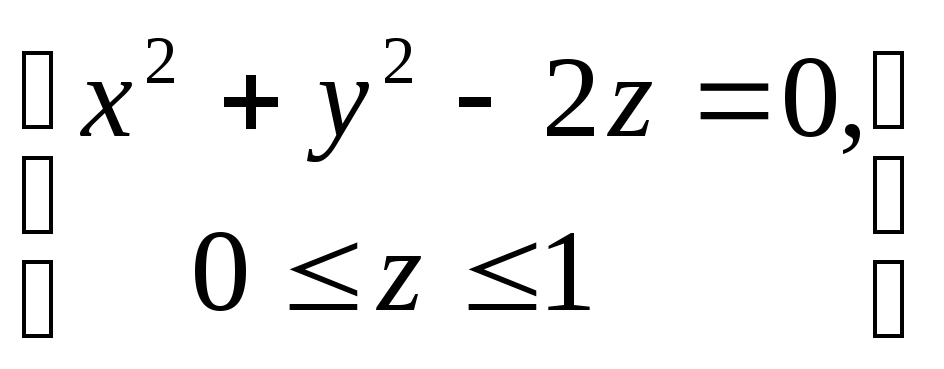13. Вычислить поверхностный интеграл IIрода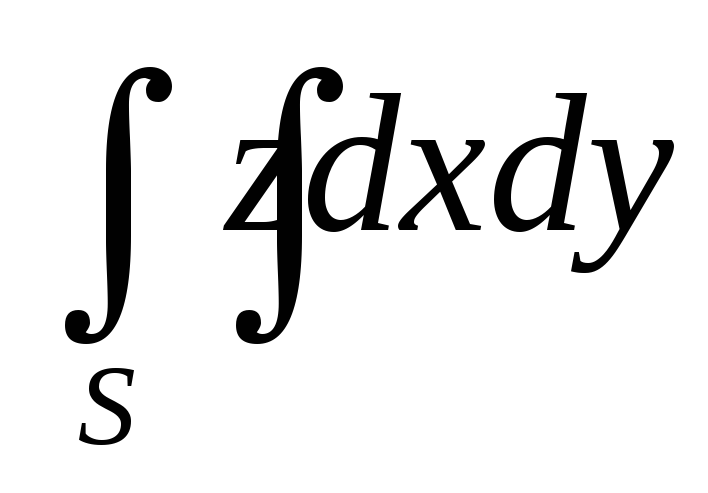, гдеS- нижняя сторона части конуса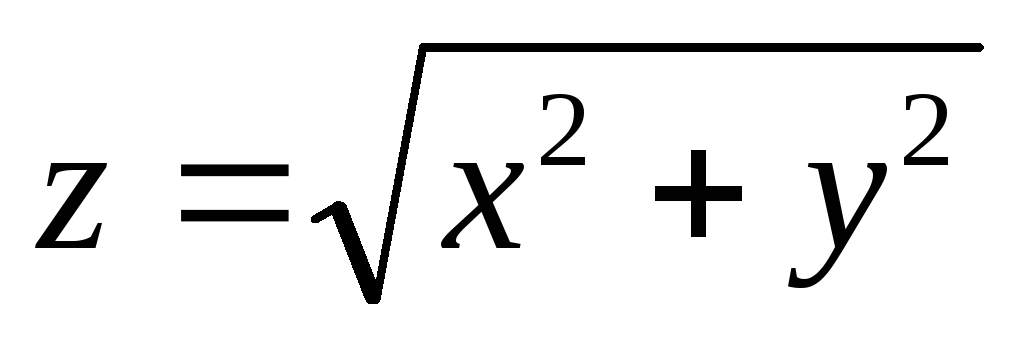, заключенного между плоскостям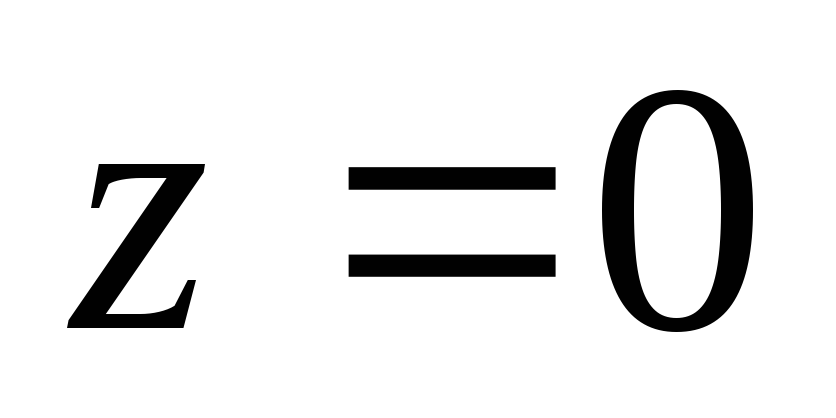ии.

Вариант 8

1. Изменить порядок интегрирования .

2. Вычислить двойной интеграл 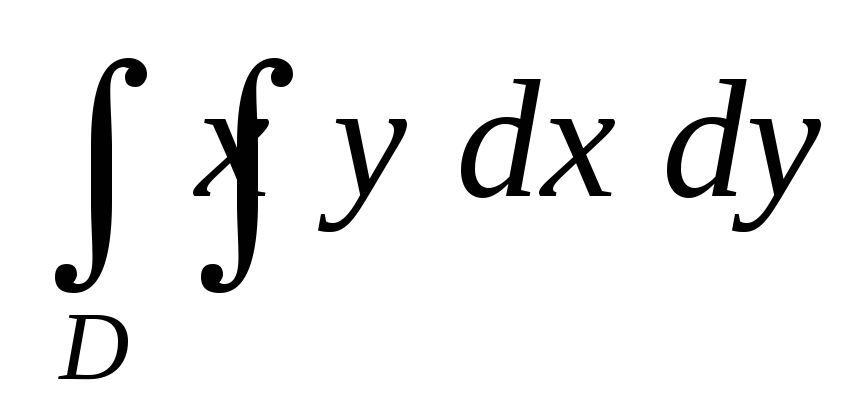по областиD, ограниченной линиями.

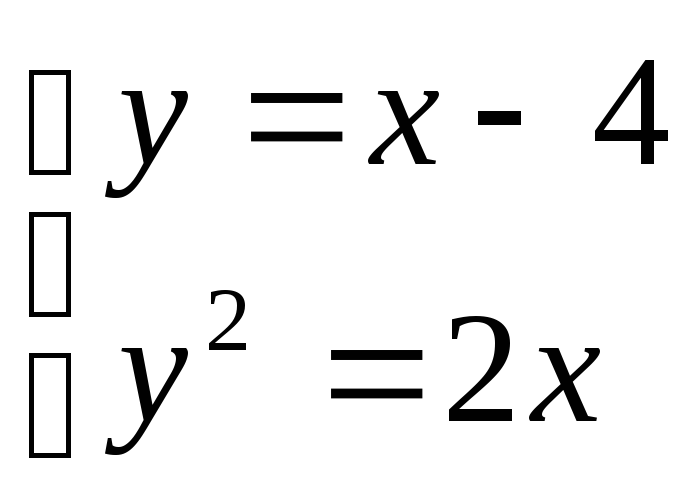3. Вычислить площадь плоской пластины D, определяемой уравнением.

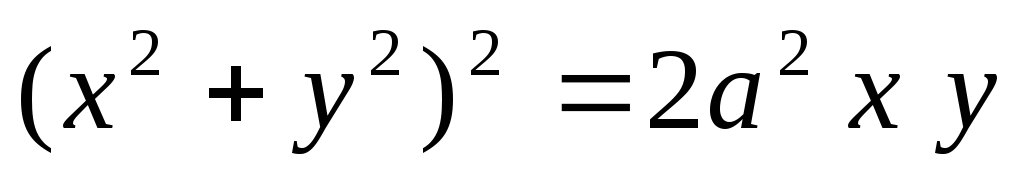4. Вычислить объем тела V, ограниченного поверхностями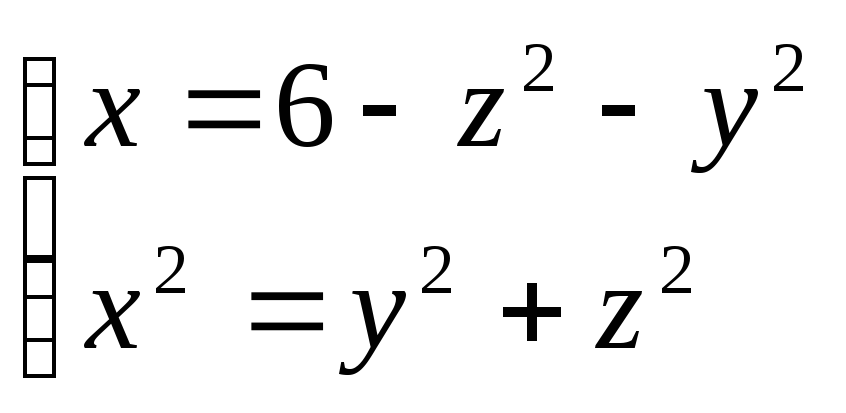. Плотность телаVсчитать равной единице.

5. Вычислить тройной интеграл 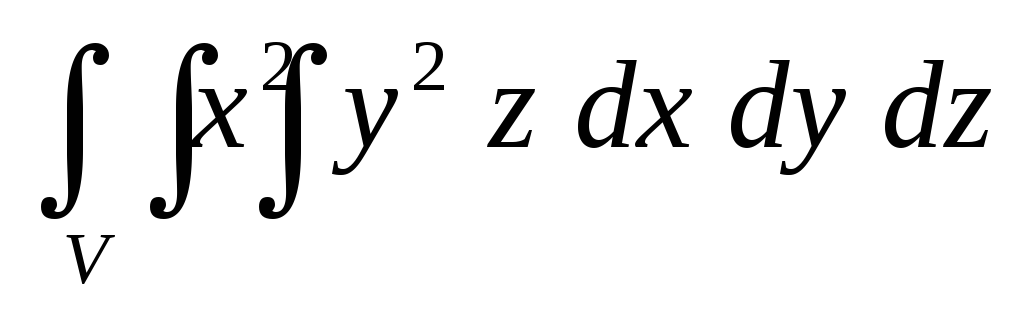по пространственной областиV, ограниченной плоскостями.

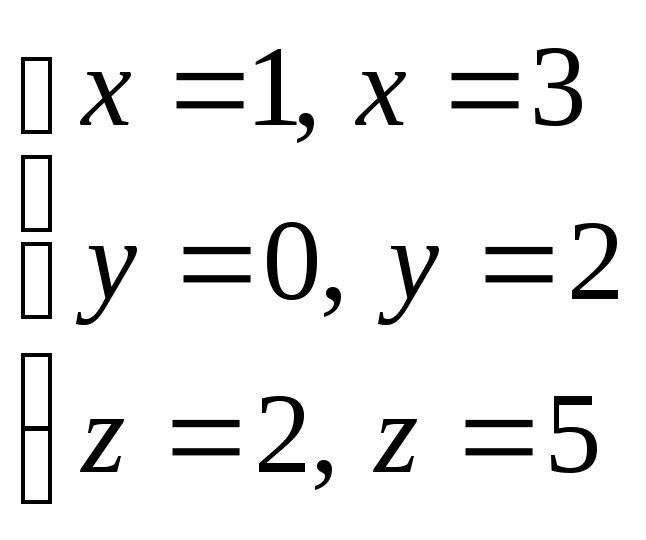6. Вычислить интеграл .

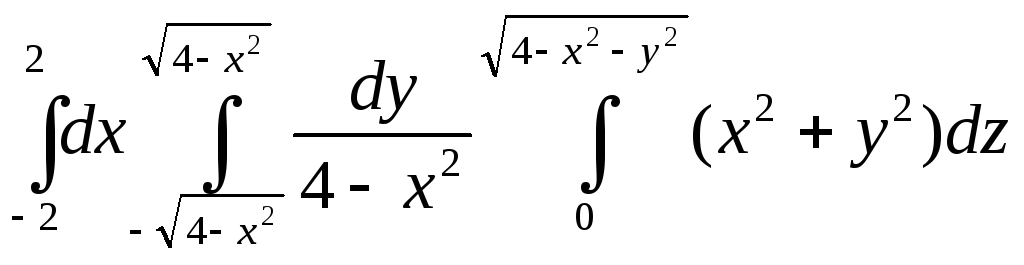7. Вычислить момент инерции круглого конуса, относительно его оси.

8. Вычислить криволинейный интеграл первого рода 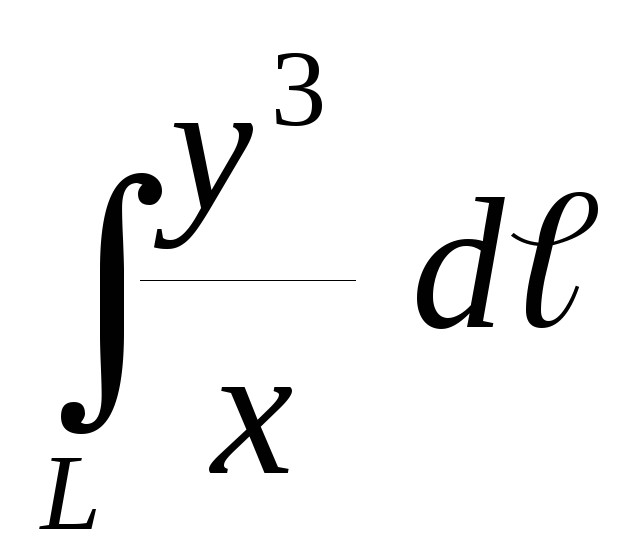по кривойL:.

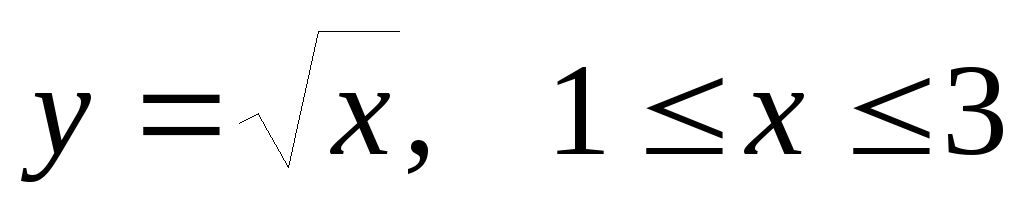9. Найти массу первого витка винтовой линии 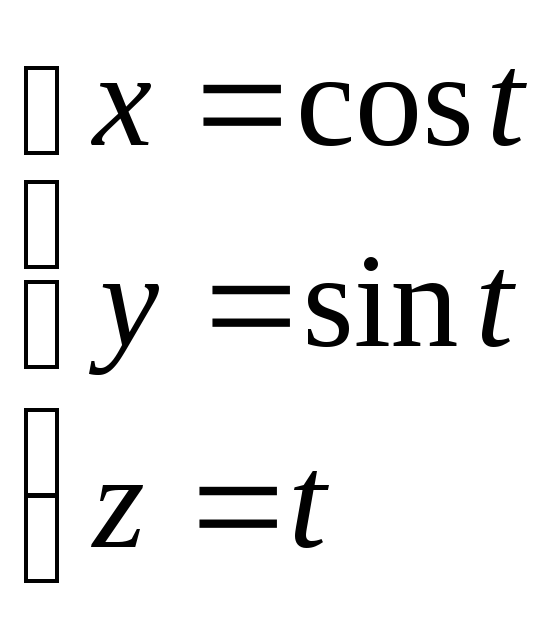плотность которой в каждой точке равна квадрату полярного радиуса этой точки

10. Вычислить криволинейный интеграл второго рода 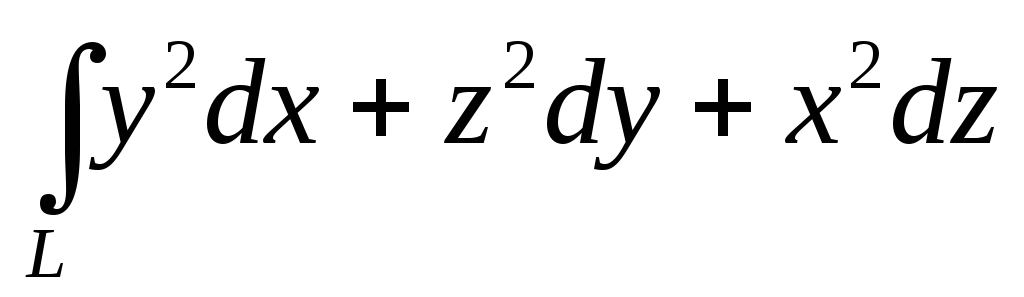, гдеL– часть кривой Вивиани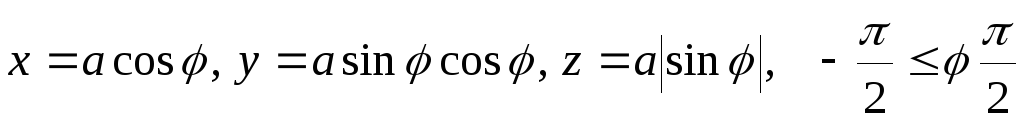при положительном направлении обхода.

11. Найти функцию по ее полному дифференциалу.

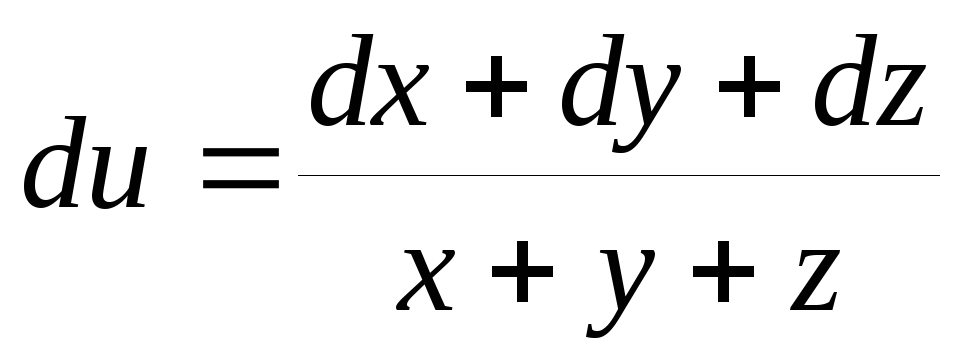12. Вычислить поверхностный интеграл первого рода 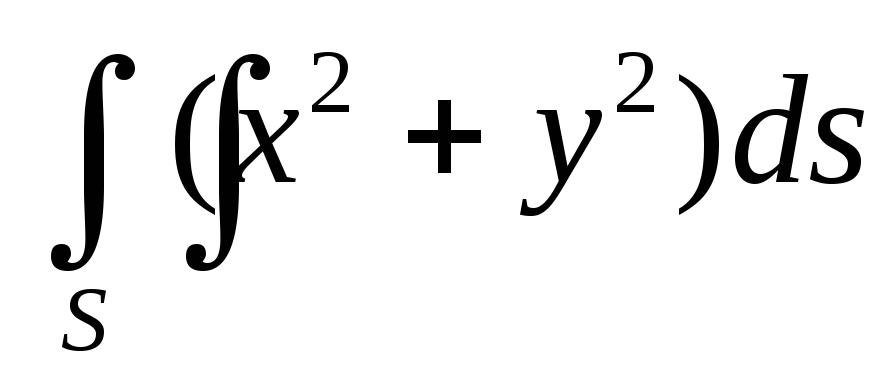по пространственной области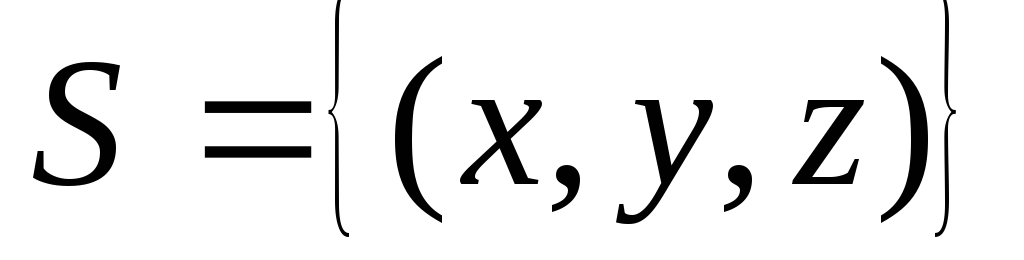, определяемой условиями.

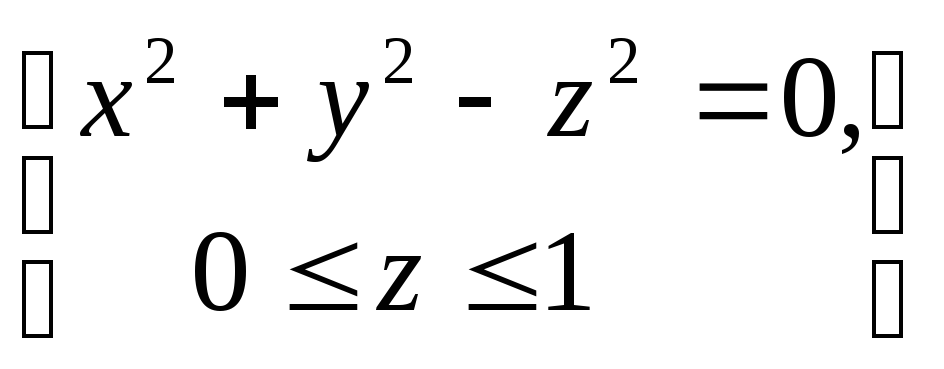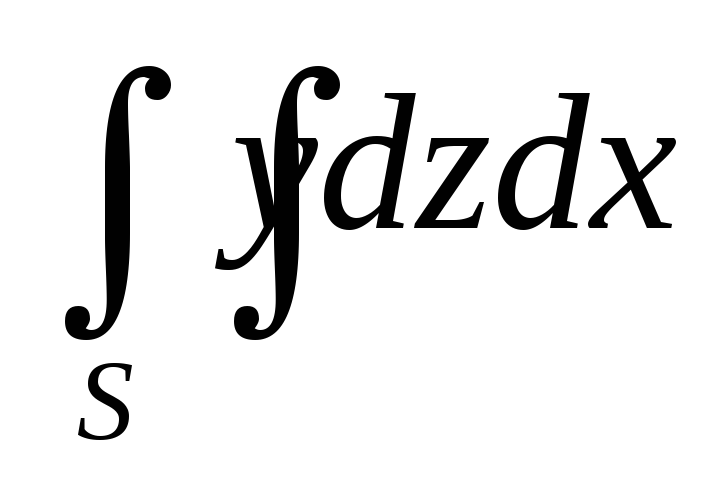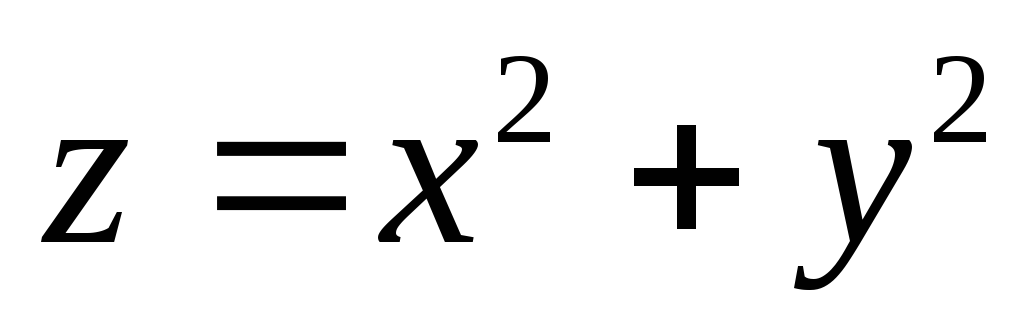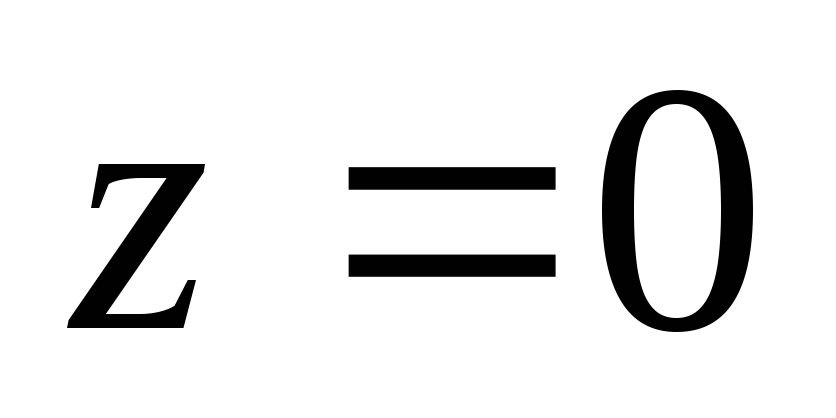13. Вычислить поверхностный интеграл IIрода, гдеS- верхняя сторона параболоида, заключенного между плоскостямии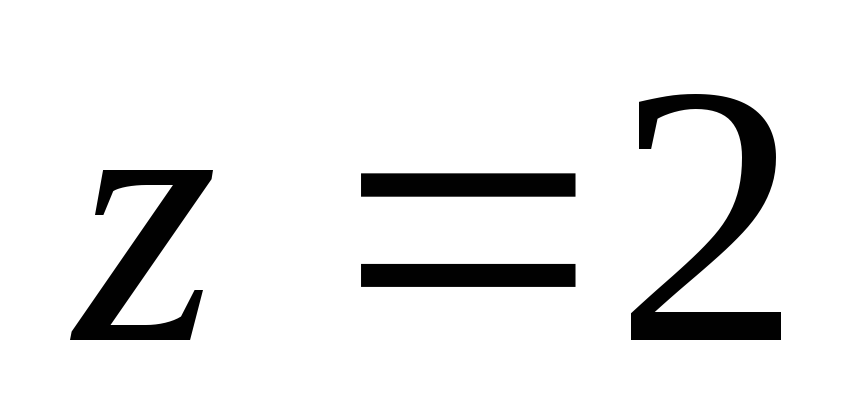.