6.2 Основное дифференциальное уравнение установившегося неравномерного плавноизменяющегося движения жидкости в открытых руслах

6.2.1 Общий случай

Рассмотрим неравномерное плавноизменяющееся движение воды в открытом канале, рис. 6.3.Применим уравнение Бернулли к двум сечениям потока 1 и 2, находящихся на бесконечно малом расстоянии dl друг от друга. Отметка дна в первом сечении z, глубина h, средняя скорость V, а во втором сечении соответственно z+dz, h+dh, V+dV (приращения отметки дна, глубины и скорости могут быть и положительными и отрицательными). С учетом введенных обозначений уравнения Бернулли принимает вид

Рис. 6.3.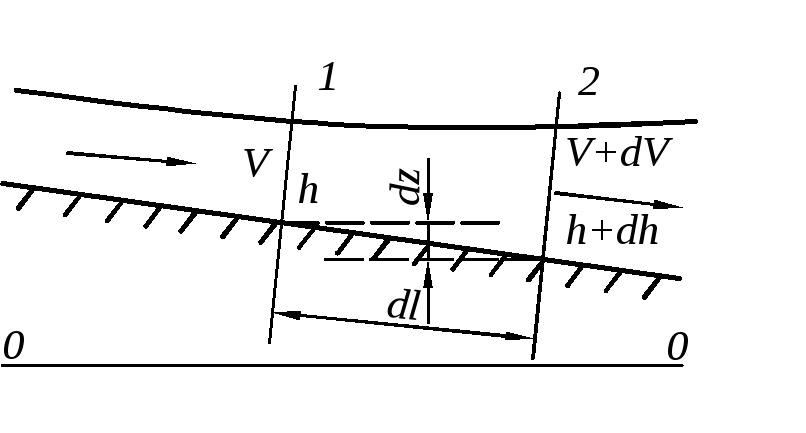

,

(6.1)

где - потери энергии по длине между расчетными сечениями.

Не учитывая величину второго порядка малости , после преобразований имеем из (6.1)

,

(6.2)

Принимая во внимание, что

и ,

разделив обе части уравнения (6.2) на dl, получим

,

(6.3)

где - уклон дна русла,- гидравлический уклон.

Уравнение (6.3) является основным дифференциальным уравнением установившегося неравномерного движения в открытом русле.

При определении гидравлического уклона в данном случае делается допущение, что потери при неравномерном плавноизменяющемся движении выражаются той же зависимостью, что и при равномерном движении, т.е.

.

(6.4)

Если при равномерном движении величина постоянна по длине потока, то при неравномерном по причине изменения глубиныh, площади сечения S, значений C и R величина также изменяется вдоль потока.

Уравнение (6.3) преобразуем так (умножив и разделив правую часть на dh)

,

или

.

Окончательно

.

(6.5)

6.2.2 Неравномерное движение в призматических руслах с прямым уклоном дна.

В призматическом русле при i > 0 движение воды с расходом Q может быть как неравномерным, так и равномерным. При равномерном движении

,

(6.6)

где величины S₀, C₀, R₀ найдены при нормальной глубине h₀.

Подставляя значение Q из формулы (6.6) в (6.4) найдём

,

(6.7)

где и- расходные характеристики при неравномерном и равномерном движении.

Подставляя (6.7) в (6.5) получим

.

(6.8)

Это уравнение является дифференциальным уравнением неравномерного плавноизменяющегося движения воды в открытых руслах с прямым уклоном дна.

6.2.3 Неравномерное движение в призматических руслах с нулевым и обратным уклоном дна

В параграфе 2 указывалось, что равномерное движение может существовать только в русле с положительным (прямым) уклоном дна. Поэтому в руслах с нулевым или обратным уклоном дна не существует нормальной глубины, и, следовательно, для них не может применяться формула (6.7) для гидравлического уклона.

Для горизонтальных участков русла (i = 0) уравнение (6.3) с учетом зависимостей (6.4) и

приводится к виду

,

(6.9)

где K_кр – расходная характеристика при критическом уклоне.

Для участков русла с обратным уклоном дна (i < 0) уравнение (6.3) с учетом зависимостей (6.4) и

может быть представлено в виде

.

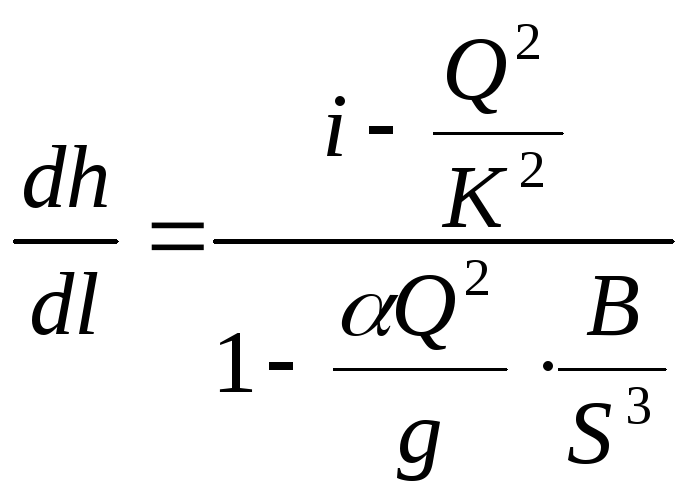При равномерном движении силы тяжести, действующие на жидкость равны силам трения, а если какая-либо причина нарушает это равновесие, то поток перестаёт быть равномерным; при этом нарушается баланс сил гидростатического давления в торцах любого выделенного отсека жидкости. Ясно, что поток жидкости предоставленный самому себе в канале, все параметры которого по длине не меняются, стремится перейти в состояние равномерного движения.
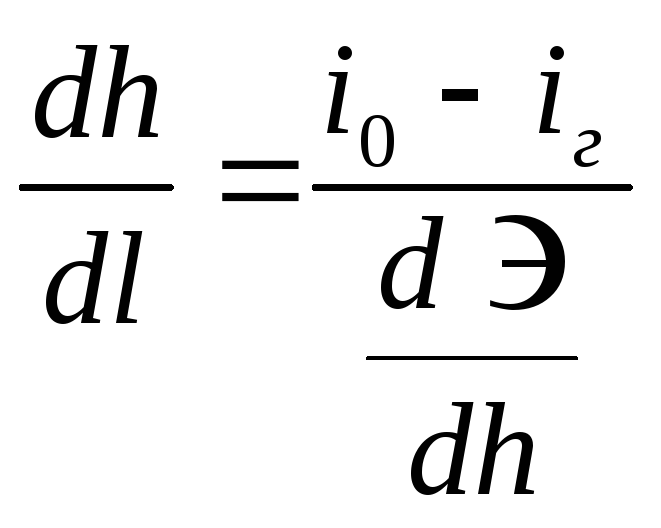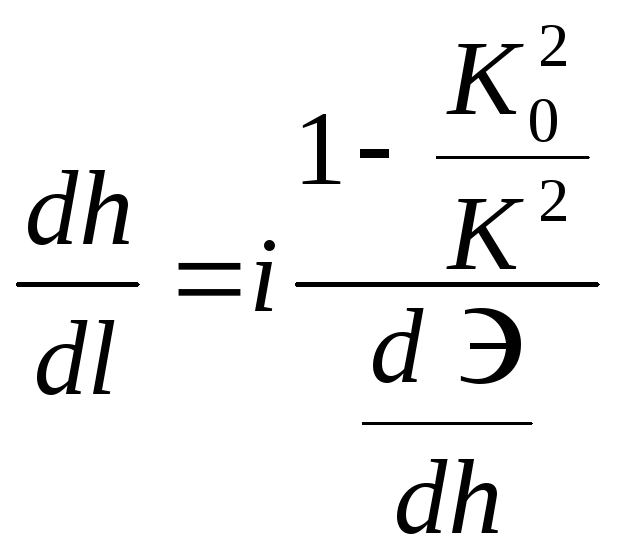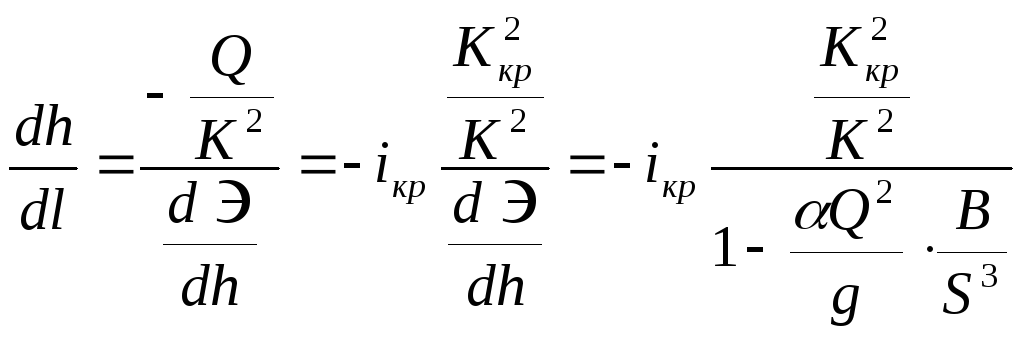