14. Гидравлический расчет открытых каналов замкнутого сечения.

Каналы, работающие при частичном заполнении сечения, встречаются в подводящих магистралях безнапорных водоводов, в канализационной сети и в различных искусственных сооружениях.

Круглые и другие криволинейные сечения безнапорных труб характеризуются той особенностью, что наибольший расход жидкости и наибольшая средняя скорость в этих сечениях имеют место не при полном, а лишь при частичном заполнении. Если в случае круглого сечения проследить за изменением величины площади живого сечения и периметра по мере увеличения степени наполнения трубы, то становятся понятными следующие закономерности.

При сравнительно малых наполнениях живое сечение растет быстро, так как возрастает ширина сечения одновременно с глубиной. Затем, после заполнения половины сечения рост площади живого сечения замедляется, т.к. с возрастанием глубины ширина сечения уже не увеличивается, а уменьшается. В последующем, для зоны, близкой к полному заполнению, рост площади живого сечения становится минимальным.

П

Рис.14.1

ри заполнении верхней части сечения смоченный периметр растет быстрее, чем площадь живого сечения, и поэтому начинает уменьшаться гидравлический радиус, что приводит одновременно и к уменьшению расхода и скорости.

Необходимо иметь ввиду, что в трубах, работающих неполным сечением равномерное движение устанавливается при достаточно большой их длине. При равномерном движении для расчетов используется формула Шези с учетом особенностей, отмеченных выше.

Расход и средняя скорость в каналах замкнутого сечения определяется по формулам:

, (14.1)

, (14.2)

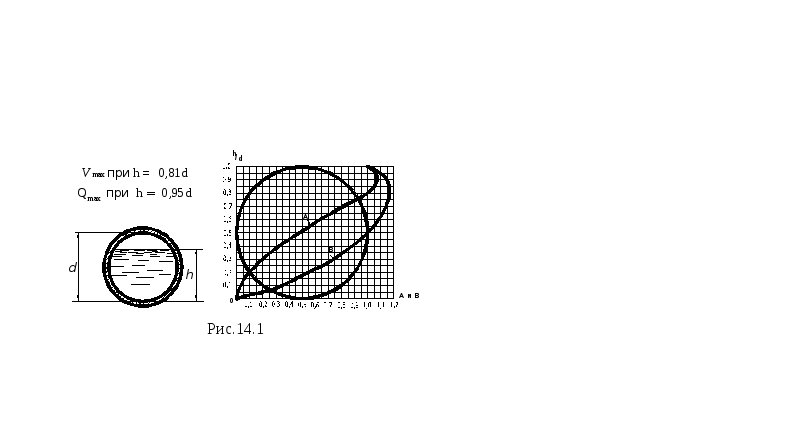где- относительная расходная характеристика,- относительная средняя скорость,- расходная характеристика и- средняя скорость при неполном заполнении. Индекс «» у величин соответствует полному заполнению.

Для круглых труб график зависимости величин А и В от относительной глубины наполнения представлен на рис. 14.1. Из графика видно, что значения А и В имеют максимум при(для А) и(для В).

В данном случае также возможно решать три задачи, аналогично трем задачам по расчету открытых каналов, причем решение задачи о нахождении расхода (первая задача) при всех остальных заданных параметрах является основным.

Для круглого сечения алгоритм решения первой задачи следующий:

1. Определяют

2. Находят (при заданных и) величину.

3. Определяют по графику на рис. 14.1 величину А.

4. Находят расход по формуле 14.1.

Если необходимо рассчитать трубы или туннели специальных форм, отличных от круговой, то применяют те же формулы (14.1) и (14.2). Величины А и В определяются по соответствующем каждой форме сечения графиком, приводимым в справочниках.

Дополнительная часть д.1 Дифференциальное уравнение неравномерного движения в призматических руслах.

Ниже приводится без подробного вывода уравнение неравномерного движения; там как в большинстве учебников оно дано именно в таком виде, считаем необходимым дать его здесь.

Применим уравнение Бернулли к двум сечениям потока 1 и 2 (в обоих течение плавноизменяющееся), расположенным на расстоянии , рис. Д.1.1; в результате получим

, (Д.1.1)

примем , раскрываем скобки в правой части последнего равенства и не учитываем(dV)² как величину бесконечно малую более высокого порядка. Значение потерь энергии на участке dl определяем так

. (Д.1.2)

В результате уравнение (Д.1.1) преобразуется к виду

,

а после деления обоих частей на dl:

(Д.1.3)

Сцелью дальнейшего преобразования полученного уравнения примем во внимание, что; расход остается постоянным вдоль потока и площадь сечения может быть представлена как. Тогда

Рис. Д.1.1

. (Д.1.4)

Если русло призматическое, то зависит только от глубины, которая в свою очередь меняется вдоль потока, т.е. зависит от, тогда

.

С учетом последнего выражения зависимость (Д.1.4) принимает вид

(Д.1.5)

Уравнение (Д.1.3) с учетом (Д.1.5) и после замены настановится таким

.

В последнем уравнении группируем члены на содержащие и на не содержащие эту производную, тогда

.

Окончательно получим

. (Д.1.6)

Это уравнение является дифференциальным уравнением неравномерного плавноизменяющегося движения жидкости в открытых призматических каналах.

Отметим некоторые особенности основного уравнения неравномерного движения.

1. Знаменатель правой части, если его приравнять к нулю, может быть преобразовано к виду

что совпадает с уравнением для определения критической глубины. Следовательно, знаменатель обращается в ноль, когда глубина потока становится равной критической; тогда левая часть принимает бесконечное значение и возникает разрыв непрерывности.

2. В числителе уравнения (Д.1.6) – разность между геометрическим и гидравлическим уклонами. Они одинаковы при равномерном движении и при этом

3. Для случая прямоугольного открытого канала вычитаемое в знаменателе (Д.1.6) преобразуется к виду

т.е. оно является числом Фруда.

4. При h → h_o и - в этом случае свободная поверхность при неравномерном движении асимптотически приближается к свободной поверхности при равномерном движении.

5. Если h → h_кр , то ; в этом случае свободная поверхность потока при глубинах близких кh_кр резко поднимается или резко снижается, и в обоих случаях нарушается условие плавноизменяемости. Резкое увеличении глубины потока называется гидравлическим прыжком, резкое уменьшение глубины связано с водопадом.

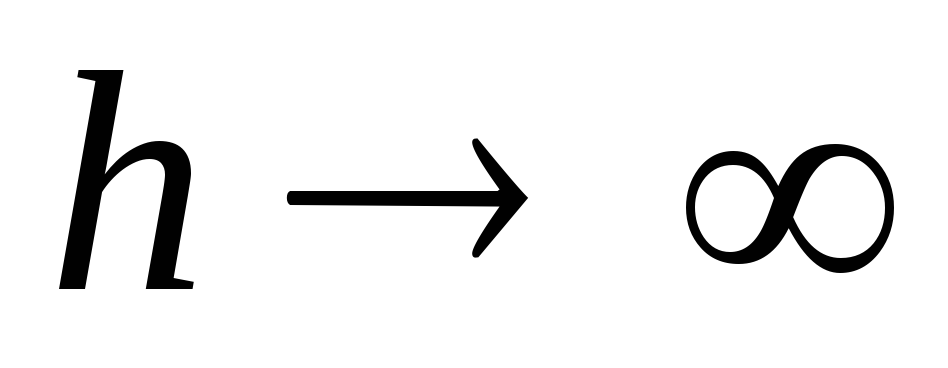6. При или призначение, так как в первом случае числитель и знаменатель уравнения (Д.1.6) обращаются в единицы, а в случаеи числитель и знаменатель принимают очень большие значения, отношение которых остается близким к единице. При этом свободная поверхность потока будет асимптотически приближаться к горизонтальной прямой.

Задача Д.1.1 Вывести дифференциальное уравнение неравномерного плавноизменяющегося движения жидкости в открытых непризматических руслах.

Указание. Учесть, что площадь сечения является функцией двух независимых переменных – глубины и ширины . Тогда

.