4.3. Свойства функции (h) и её график

Р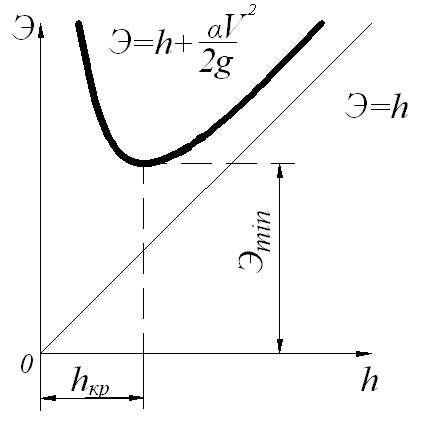ассмотрим функцию (h) и выполним анализ её зависимости от глубины h потока для заданной формы поперечного сечения и при Q=const. Удельную энергию сечения (4.1)

(h)=h+

м

Рис.4.4.

ожно рассматривать состоящей из двух частей: удельной потенциальной энергией _пот.=h и удельной кинетической энергии _кин.== (учтено, что V=).

Из уравнения неразрывности Q=VS=const следует, что если глубина h увеличивается (а следовательно увеличивается и площадь сечения S), то скорость уменьшается и наоборот, при уменьшении h скорость увеличивается. Поэтому тенденции изменения _пот и _кин с изменением h противоположны, а именно

если h 0, то  и (h),

если h, то  0 и (h).

Следовательно, график функции (h) в координатах (h;) должен иметь вид кривой с двумя ветвями, уходящими в бесконечность при h 0 и при h, рис. 4.4. При этом _пот=h будет иметь вид биссектрисы координатного угла, а _кин - вид кривой второго порядка. График функции (h) асимптотически приближается к биссектрисе угла и к вертикальной оси ординат (оси ); очевидно, поэтому, что при некотором значении h функция (h) принимает минимальное значение.

При h=h_кр функция (h) принимает минимальные значения и следовательно h=h_кр является точкой экстремума. Из курса высшей математики известно, что при прохождении точки экстремума производная меняет знак. Следовательно и в нашем случае производная d/dh будет менять знак при переходе через h=h_кр. Действительно, как следует из рисунка 4.4. d/dh<0 при h<h_кр, т.е. для бурных потоков и d/dh>0 при h>h_кр, т.е. для спокойных потоков

Задача 4.1. Указать вид графика функции (h)=h+ в системе координат ( -h), т.е. оси ординат откладывается h, а по оси абсцисс (h).

5. Критическая глубина. Критический уклон

5.1 Критическая глубина

Глубина потокаh, при которой удельная энергия сечения для заданного расхода в данном русле принимает минимальное значение, называется критической глубиной h_кр.

Согласно рис. 5.1 точка на графике, соответствующая глубине, равной критической делит график удельной энергии на левую часть, где h<h_кри правую, гдеh>h_кр.

Введение критической глубины позволяет делить потоки жидкости на 3 группы:

1. Спокойные потоки, для которыхh>h_кр;

2. Бурные потоки, для которыхh<h_кр;

3. Потоки в критическом состоянии, для которых h=h_кр.

Определение состояния потока (спокойное или бурное) может поэтому производиться сравнением фактического значения h с h_кр.

Чтобы найти h_кр примем во внимание, что при h=h_кр производная от Э по h равна нулю, т.е. приh=h_кр.

Подсчитаем производную

(учли (1.7) ).

Подставим в последнее соотношение h_кр вместо h и приравняем его к нулю, тогда

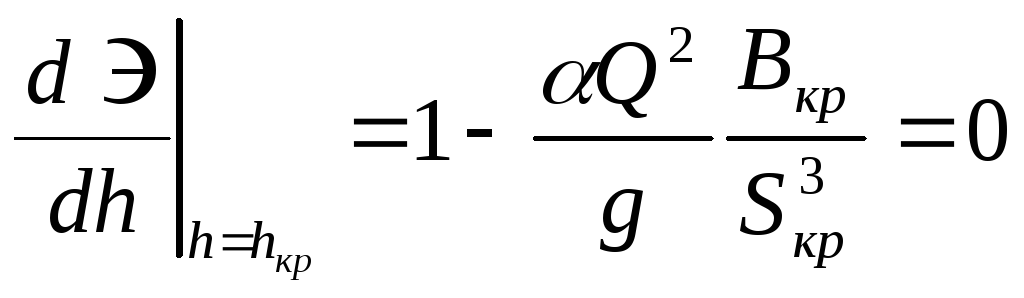. (5.1)

Уравнение для определения величины h_кр, следует из (5.1), которое преобразуется перенесением в одну часть членов, не зависящих от h_кр, а в другую – всех величин, зависящих от h_кр

. (5.2)

Последнее уравнение (5.2) иногда называют уравнением критического состояния. Для русла любого сечения в общем виде оно решается подбором, графоаналитически или на ЭВМ.

Замечание 5.1. Как следует из уравнения (5.2), критическая глубина не зависит ни от уклона, ни от шероховатости русла (канала).

Задача 5.1. Найти выражение для критической глубины потока в прямоугольном русле.

Решение. Для прямоугольного русла b=b_кр=const, S_кр=bh_кр; тогда уравнение (5.2) примет вид

откуда.

Задача 5.2. Для канала прямоугольного сечения найти минимальную величину удельной энергии сечения и значение критической скорости V_кр.

Решение. Для решения первой части задачи достаточно из формулы

значение , равноеподставить в выражение для удельной энергии сечения, т.е. в критическом состоянии удельная энергия потока в прямоугольном русле равна. Значение дляV_кр имеет вид .