6.3. Анализ кривых свободной поверхности

6.3.1 Общие положения

При анализе кривых свободной поверхности обычно сравнивают глубины потока с двумя основными характерными глубинами – нормальной и критической. В связи с этим над дном русла различают условные зоны, образованные линиями этих глубин, рис. 6.4, N-N – линия нормальных глубин, K-K – линия критических глубин

Рис.6.4

На рис. 6.4. а) изображен канал с уклоном дна меньше критического и при равномерном движении поток находится в спокойном состоянии, h₀ > h_кр. На рис 6.4. б) – канал с уклоном дна больше критического; при равномерном течении поток в нем находится в бурном состоянии, h_кр > h₀. На рис.6.4. с) – поток в критическом состоянии, при этом h₀ = h_кр. Как видно из рисунка 6.4, получаются следующие зоны, в которых может располагаться кривая свободной поверхности: зона a – выше линии NN и KK;зона b – между линиями NN и KK; зона с – ниже линий NN и KK.

Рассмотрим некоторые общие особенности изменения глубин при неравномерном движении.

Если глубина потока при неравномерном движении стремится к нормальной глубине (), тои, согласно уравнению (6.8). Это значит, что глубина стремится стать постоянной по длине потока, т.е.кривая свободной поверхности асимптотически приближается к линии нормальных глубин.

Если глубина потока при неравномерном движении приближается к линии критических глубин (), то знаменатель уравнения (6.8) стремится к нулю, а, т.е. функция глубины терпит разрыв непрерывности и кривая свободной поверхности теоретически будет подходить по перпендикуляру к линии критических глубин. На самом деле кривая свободной поверхности подходит к линии критических глубин под большим углом. Это объясняется тем, что в области глубин, близкой к критической глубине, значительно увеличивается кривизна линий тока и нарушается условие плавноизменяемости движения. В этом случае уравнение Бернулли и вытекающее из него уравнение (6.8) неточно отражают действительное течение.

В результате сделанных замечаний сформулируем характерные особенности неравномерного движения.

1. Кривые свободной поверхности подходят асимптотически к линии нормальных глубин;

2. Кривые свободной поверхности подходят под крутым углом к линии критических глубин;

3. При весьма больших глубинах свободная поверхность стремится стать горизонтальной.

Если уклон дна русла равен критическому уклону, т.е. h₀ = h_кр, перечисленные особенности не имеют места, так как кривая свободной поверхности не может одновременно асимптотически подходить к линии нормальных глубин и пересекать ее под большим углом.

Рассмотрим различные формы кривых свободной поверхности, учитывая общие особенности, уклон дна русла и соотношения между глубиной неравномерного движения, нормальной и критической глубинами.

Предварительно, учитывая рис.5.1, заметим, что при спокойном состоянии потока , а при бурном состоянии.

6.3.2 Уклон дна русла меньше критического (i < i_кр)

В этом случае h₀ > h_кр, т.е. линия нормальных глубин N-N проходит выше линии критических глубин, рис. 6.4, а). Неравномерное движение может устанавливаться в трех зонах:

а) при h > h₀;

b) при h₀ > h >h_кр;

с) при h < h_кр.

Зона a. При этом h > h₀, K > K₀ и h >h_кр, а .Следовательно, и числитель и знаменатель в (6.8) положительны и сама величинаположительна. Это означает, что глубина вдоль движения возрастает. В зонеа глубина может изменяться от нормальной глубины h₀ до значительно большей. В левой части зоны кривая свободной поверхности асимптотически приближается к линии нормальных глубин, а в конце при больших глубинах стремится стать горизонтальной, рис. 6.5.

Рис. 6.5. Рис. 6.6.

Такая кривая называется кривой подпора типа а1. Примером такой кривой является кривая свободной поверхности перед плотиной или другой преградой в русле, рис. 6.6.

Зона b. В этом случае h < h₀, K < K₀ и h >h_кр, при этом . Производная, как это следует из уравнения (6.8) имеет отрицательный знак, т.е.. Глубина вдоль потока уменьшается от нормальной до критической глубины. Так как к линии нормальной глубины кривая свободной поверхности приближается асимптотически, а к линии критической глубины под крутым углом, то эта кривая имеет выпуклую форму и называетсякривой спада типа b1, рис. 6.5. Такая кривая может установиться, например, перед уступом (перепадом) в дне русла, рис. 6.7. В конце такой кривой (над уступом) теоретически должна

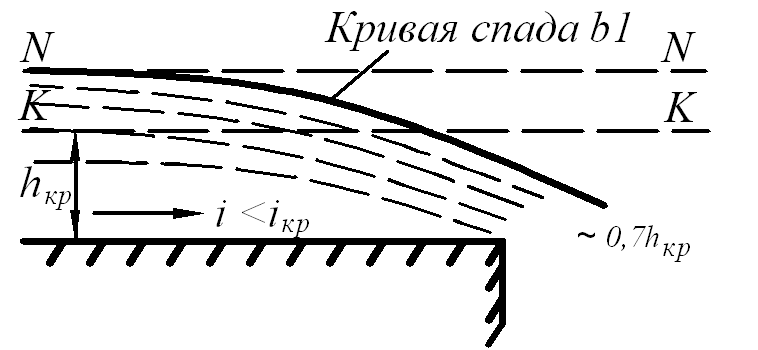
Рис. 6.7. Рис. 6.8.

установиться критическая глубина, однако опыты показывают, что она устанавливается на некотором расстоянии до уступа. Обычно при спокойном состоянии потока над стенкой падения устанавливается глубина, равная h_ст = 0,7h_кр, а при бурном состоянии потока – глубина, практически равная нормальной h_ст = h₀, что может быть объяснено отклонением движения в области, близкой к критической глубине, от условий плавноизменяющегося движения.

Зона с. В этом случае h < h_кр< h₀, а K < K₀, . Производная, согласно уравнению (6.8) положительна, т.е.. Следовательно, глубина вдоль потока возрастает от какой-то начальнойh < h_кр до критической глубины, рис. 6.5. Кривая свободной поверхности вогнута и называется кривой подпора типа с1. Такая кривая может установиться непосредственно за плотиной или при истечении из-под щита, рис. 6.8.

6.3.3 Уклон дна русла больше критического (i > i_кр)

В этом случае линия нормальных глубин N-N проходит ниже линии критических глубин K-K, рис. 6.4. б). Рассмотрим особенности неравномерного движения в зонах a), b), c).

Зона a. В данном случае h > h_кр> h₀, а K > K₀, . При этом производнаяпо уравнению (6.8) получается положительной, и следовательно, глубина вдоль потока возрастает и имеет место выпуклая кривая подпора типаaII, подходящая под крутым углом к линии критических глубин и стремящаяся стать горизонтальной при больших глубинах. Кривая подпора aII образуется ниже гидравлического прыжка по течению, через который происходит переход потока из бурного состояния в спокойное, рис. 6.9.

Рис. 6.9 Рис. 6.10

Зона b. При этом h < h_кр, а иh > h₀, K > K₀. Производная будет отрицательной, т.е. кривая свободной поверхности является кривой спада. Она имеет вогнутую форму и называетсякривой спада bII. Такая кривая устанавливается после изменения уклона дна русла от значения меньше критического к значению уклона больше критического, рис. 6.10. На рисунке 6.10 показан такой переход от канала с уклоном i₁ меньше критического к началу с уклоном i₂ большем критического; критическая глубина при переходе остается неизменной.

Зона с. В этом случае h < h₀< h_кр, K < K₀ и . Из уравнения (6.8) следует, что производная будет положительной и, следовательно, глубины будут повышаться вдоль движения, асимптотически приближаясь к значению нормальной глубиныh₀. Такая кривая свободной поверхности называется кривой подпора типа сII.