Д.4.2 Число Фруда как безразмерный критерий.

В научных и инженерных приложениях исключительно универсальным является метод анализа размерностей (см.например Физические свойства жидкостей. Метод анализа размерностей.Часть I). Одним из центральных понятий метода анализа размерностей является - теорема. Согласно- теореме уравнение, выражающее некоторую физическую закономерность и содержащееразмерных величин (из которыхвеличин имеют независимые размерности), может быть преобразовано в уравнение, связывающее () независимых безразмерных комплексов. Эти безразмерные комплексы составлены из указанныхвеличин.

Независимыми называются комплексы, которые не могут быть получены в виде степенной функции остальных комплексов.

В гидравлике в качестве параметров с независимыми размерностями принимают базовые величины: характерный линейный размер, время и массу. Размерность любой гидравлической величины может быть выражена через размерности базовых величин. Иногда в качестве базовых величин выбирают линейный размер, скорость и плотность.

Если произвольную гидравлическую величину, не входящую в состав параметров с независимыми размерностями, обозначить через , то безразмерный комплекс, характеризующий влияние данной размерной величинына движение жидкости (-член), выражается как

(Д.4.2.1)

где ,,- размерности длины, массы, времени соответственно. Напомним, что размерности базовых величин таковы

, ,.

Определим - член, отражающий влияние силы тяжести (т.е. ускорение силы тяжести). Для этого применим (Д.4.2.1)

или .

Тогда .

Решая систему, получим ,,.

Откуда - член , отражающий влияние силы тяжести на движение жидкости, равен

.

Этот безразмерный комплекс называется числом Фруда. В зарубежной литературе часто применяют число Фруда в виде

.

Д.5 Спокойные и бурные потоки в каналах переменного сечения.

Д.5.1 Изменение параметров спокойных и бурных потоков при расширении и сужении русла.

Рассмотрим как меняются скорости и глубины струйного потока при изменении его сечения.

Для этой цели возможно использовать уравнение (Д.1.10), но для качественной характеристики вполне достаточно упрощенной схемы растекания струйного потока идеальной жидкости по горизонтальному дну, рис. Д.5.1. Рассмотрим отдельную струйку конечной ширины b, скорость в пределах которой равна u, а глубина h. Выберем два сечения струйки, расположенные на бесконечно малом расстоянии друг от друга. Для решения задачи применим уравнение неразрывности и уравнение Бернулли.

Уравнение неразрывности имеет вид

(Д.5.1)

Д

uu

b

ля получения уравнения, отражающего бесконечно малые изменения параметров вдоль струйки, продифференцируем (Д.5.1) как произведение 3-х переменных величин, в результате получим

,

так как , то допустимо разделить обе части последнего уравнения на,

т

Рис. Д.5.1

огда

(Д.5.2)

Уравнение Бернулли для двух выбранных сечений с учетом горизонтального дна и того, что жидкость идеальная имеет вид

или (Д.5.3)

Преобразуем (Д.5.2) разделив обе его части на du

,

и далее, оставим слагаемые с db в левой части, а остальные вынесем в правую часть

,

умножим обе части последнего уравнения на b и вынесем в правой части за скобку

(Д.5.4)

Для дальнейших преобразований из уравнения Бернулли выразим производную и в скобках (Д.5.4) вместоподставим; в результате получим

или

Из последнего уравнения получаем окончательно

. (Д.5.5)

Выполним анализ (Д.5.5) для случая расширения спокойного и бурного потоков.

1. Поток спокойный, Fr < 1, db > 0 (так как поток расширяется и приращение ширины положительное). Уравнение (Д.5.5) преобразуем, умножая левую и правую части на db, к виду

(Д.5.6)

так как величина в скобках отрицательная и db > 0, то правая часть отрицательна и, следовательно, левая часть также отрицательна, т.е. и, таким образом, при расширении спокойного потока скорость в нем убывает.

2. Поток бурный. При этом Fr > 1, db > 0 и в уравнении (Д.5.6) правая часть положительна; тогда и , т.е. приращение скорости положительно и, следовательно, при расширении бурного потока скорость его возрастает.

Для анализа функции h = h (b) поступаем аналогично: применяем уравнение (Д.5.2), решаем его относительно и учитываем зависимость (Д.5.5). Окончательно получаем

(Д.5.7)

Анализ уравнения (Д.5.7) показывает: в спокойном потоке при увеличении его ширины глубина увеличивается, так как Fr < 1 и ; в бурных потоках расширение ведет к уменьшению глубины (Fr > 1 и ).

Все полученные результаты сведены в таблицу 1 (для прямоугольного канала).

Таблица 1

Изменение ширины потока	Состояние потока	Изменение
		Глубины	Скорости
(расширяющийся поток)	Спокойный Fr < 1
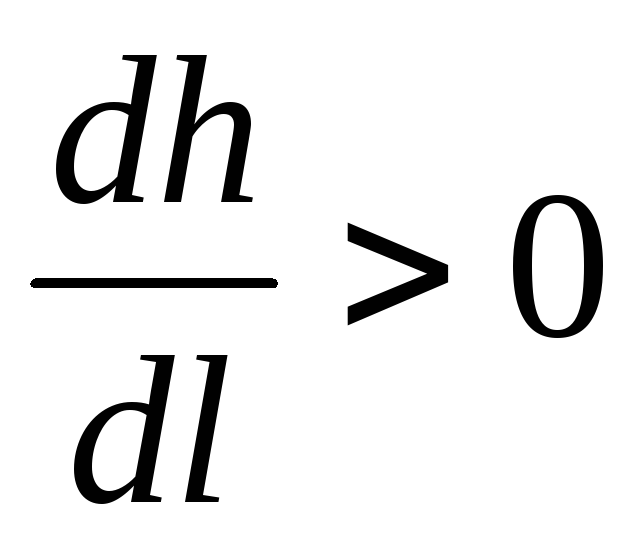
	Бурный Fr > 1
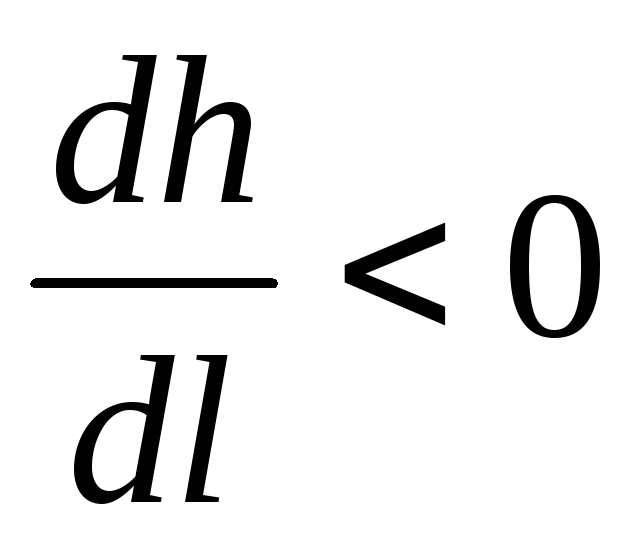
(сужающийся поток)	Спокойный Fr < 1
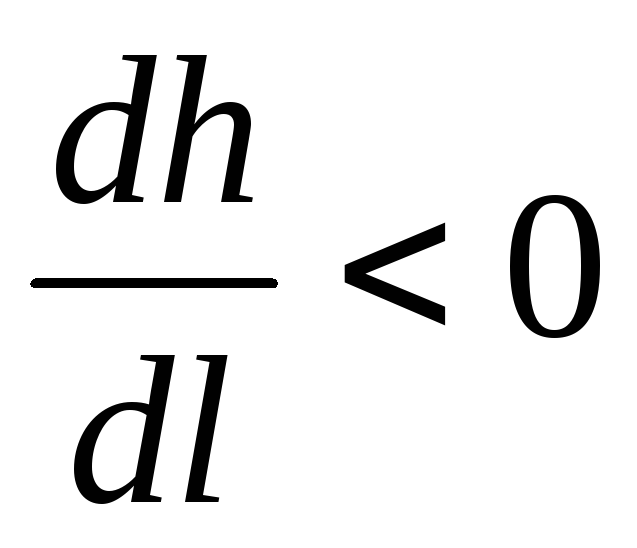
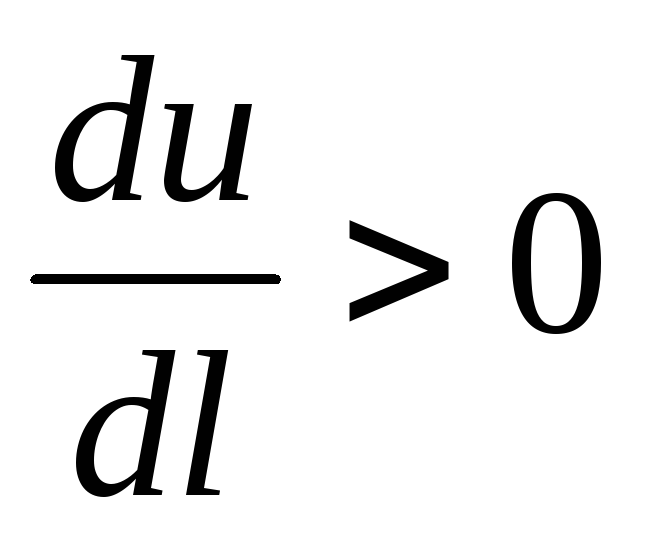
	Бурный Fr > 1

Так как движение рассматривается как одномерное, результаты анализа позволяют судить лишь об изменении осредненных значений глубин и скоростей в сечениях канала. Полученные результаты могут иметь практические значение; например, за дорожными водопропускными трубами поток обычно находится в бурном состоянии, затем расширяется в отводящем канале и скорость его увеличивается. Таким образом при проектировании отводящих каналов необходимо обращать особое внимание на выбор крепления русла.