Д.2 Построение кривых свободной поверхности интегрированием уравнения неравномерного движения.

Так как дифференциальное уравнение неравномерного планоизменяющегося течения в открытых руслах(Д.1.6) достаточно точно описывает зависимость между всеми параметрами потока, то естественно его проинтегрировать для решения задачи построения кривых свободной поверхности. Напомним, что уравнение (Д.1.6) имеет вид

.

Если известны уклон дна канала , расход, коэффициент шероховатостиn, все геометрические параметры сечения, то правая часть последнего уравнения представляет собой функцию только глубины потока , т.е.

, (Д.2.1)

а уравнение (Д.1.6) представляется так

. (Д.2.2)

Переменные в (Д.2.2) разделяются

. (Д.2.3)

Возьмем интегралы от правой и левой частей (Д.2.3)

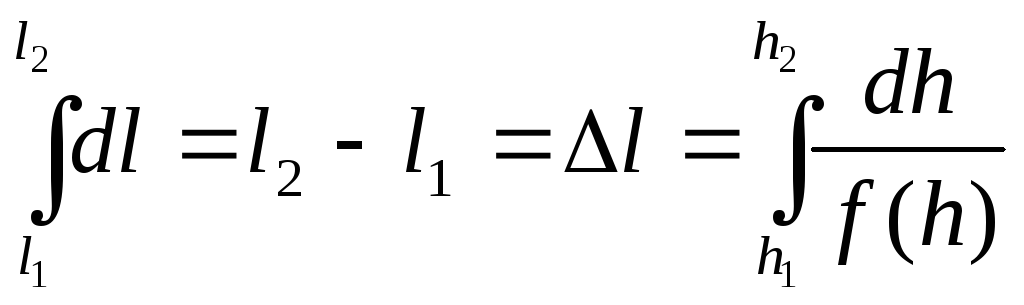, (Д.2.4)

где принято: при глубина равнаи приглубина равна,- расстояние между сечениями с глубинамии. Задача будет решена, если каким-либо численным методом найти величину интеграла в (Д.2.4); это действие никаких принципиальных затруднений не представляет и в настоящих условиях на ЭВМ решается легко.

Д.3 о расчете водослива.

Значения коэффициентов расхода водосливов находятся в основном в результате опытов; здесь изложен иной подход к расчету параметров потока при истечении через водослив.

По определению любой водослив представляет собой преграду в потоке жидкости. Очевидно, что поток воздействует на преграду с определенной силой; с такой же силой и преграда действует на поток. Для определения скоростей и глубин перед и за водосливом необходимо связать параметры потока с силой, действующей со стороны потока на водослив (преграду). Такой подход может привести к более точным и исчерпывающим результатам, чем с помощью обычного полуэмпирического подхода; в данном случае основной неизвестной величиной является сила, действующая на преграду.

В качестве уравнения для расчета параметров потока при истечении через водослив может служить уравнение сохранения количества движения в интегральной форме (течение установившееся)

,

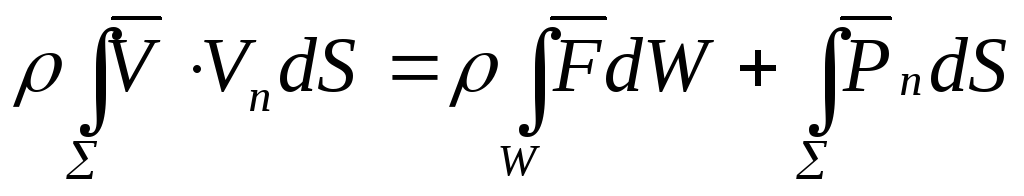где - объем, ограниченный контрольной поверхностью;- результирующий вектор объемных сил;- вектор поверхностных сил, действующих на элемент поверхностис внешней нормалью;- вектор скорости внутри или на границе области;- составляющая векторапо нормали кв данной точке.

Данный подход может оказаться полезным, например, при расчете подпора от промежуточных мостовых опор на водотоке.

Д.4 Число Фруда. Д.4.1 Число Фруда как параметр подобия потоков.

Рассмотрим движение несжимаемой жидкости в поле силы тяжести. Условия динамического подобия двух потоков можно получить, представив уравнения Навье-Стокса в безразмерной форме. Первое из уравнений Навье-Стокса для несжимаемой жидкости имеет вид (Основные уравнения динамики. Часть 3)

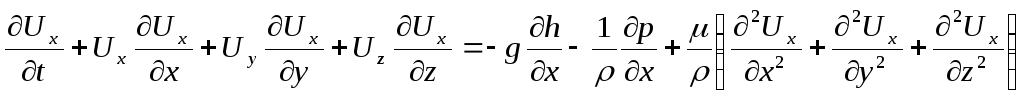.(Д.4.1.1)

Это уравнение может быть преобразовано с помощью безразмерных (не имеющих наименования ни в какой системе) величин, определенных так

, ,,,,, (Д.4.1.2)

, ,,,,.

В этой системе величин и- постоянные значения длины и скорости, выбранные как характеристики течения. Например, если определяется сила при обтекании шара потоком жидкости, то в качественеобходимо выбрать диаметр сферы, а в качестве- скорость набегающего потока.

Если подставить выражения (Д.4.1.2) в уравнение (Д.4.1.1), то получим следующее уравнение

. (Д.4.1.3)

Как выясняется при проверке, эти подстановки не изменили размерности любого слагаемого уравнения (Д.4.1.1) – любой член этого уравнения имеет размерность ускорения(силы, отнесенной к единице массы). Уравнение (Д.5.1.3) можно сделать безразмерным, разделив каждый его член на ; в результате получим

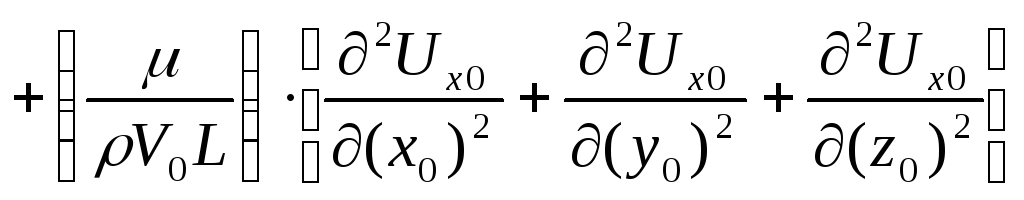. (Д.4.1.4)

Так как все величины с индексом 0 безразмерны (это ,,,,и т.д.), то каждый из двух комплексов, находящихся в виде коэффициентов при первом и третьем членах в правой части уравнения (Д.5.1.4) и содержащих масштабные величиныи, должен быть также безразмерным.

Первый безразмерный комплекс получается делением ускорения свободного падения на некоторую силу, отнесенную к массе

. (Д.4.1.5)

Число, обратное (Д.4.1.5) и равное

называется числом Фруда.

Число Фруда является важным параметром, когда силы тяжести оказывают решающее влияние на течение потока.