9. Число Фруда как отношение скоростей.

На свободной поверхности могут возникать гравитационные волны и поведение свободной поверхности зависит от отношения скорости потока к скорости распространения волн. Скорость распространения малых гравитационных волн (малых возмущений) на поверхности потока, глубина которого мала по сравнению с длиной волны определяется по формуле (10.8)

.

Тогда получаем безразмерное отношение

,

где число называется числом Фруда.

Если , то скоростьназывается критической скоростью. Дляскоростьи поток называется спокойным (докритическим).

Для скоростьи поток называется бурным (сверхкритическим).

При изменении глубины изменяется и скорость распространения волн, поэтому число Фруда, в каналах переменной глубины или при обтекании препятствий потоком, возможно интерпретировать как отношение квадрата местной скорости потока к квадрату местной скорости распространения малых возмущений.

10. Волновые движения жидкости.

10.1 Основные понятия и определения.

С физической точки зрения разнообразие волн на воде велико, например, штормовые волны в океане, вызванные ветром, волны паводка на реках, корабельные волны, волны цунами, приливные волны и т.д.

С математической точки зрения, очевидно, что общего решения, охватывающего все возможные случаи, не существует. Главная трудность изучения волн на воде заключается в том, что одна из границ, а именно – свободная поверхность – является одной из неизвестных величин. Существуют два различных типа волн на воде – колебательные волны и волны перемещения. В колебательной волне расход жидкости равен нулю; волновые движения аналогичны поперечным колебаниям шнура. К этому типу волн относятся волны от брошенного в воду предмета, корабельные волны. В волне перемещения, как видно из названия, происходит перенос жидкости в направлении движения волны. Волной перемещения является, например, движущийся гидравлический прыжок.

Ещё раз необходимо подчеркнуть, что волны – это распространяющиеся колебания. В положении равновесия поверхность волны представляет горизонтальную плоскость. Если каким- то образом вывести из положения равновесия хотя бы незначительную часть поверхности воды, например, бросить камень, то это “возмущение” будет распространяться в виде волны. В данном случае колебания поверхности являются результатом взаимодействия двух факторов: силы, возвращающей в положение равновесия, и инерции, заставляющей проскакивать это положение равновесия.

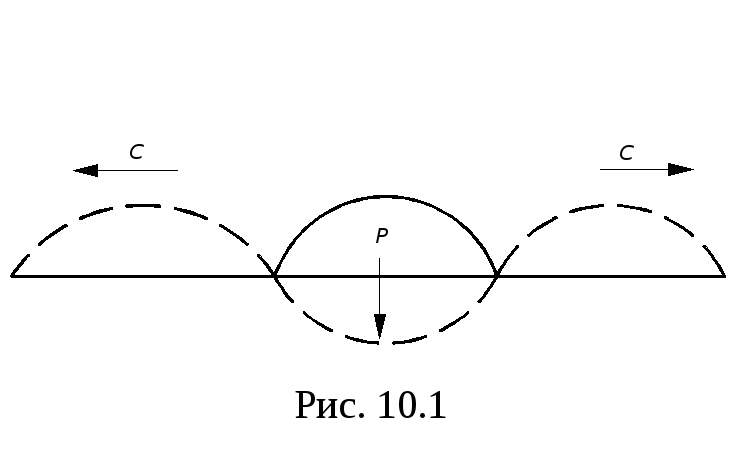
Если на поверхности жидкости образуется «горб» (возвышение), то вернуть частицы жидкости в положение равновесия может, например сила тяжести P, рис. 10.1, пропорциональная ускорению свободного падения g. Двигаясь вниз, по инерции “горб” пройдёт ниже положения равновесия; рядом с ним будет вытеснен другой “горб” и т.д., в результате чего пробежит волна, характеризуемая некоторой скоростью и длинной(расстояние между горбами).

Заметим, что колебания происходят в вертикальной плоскости, а волны распространяются в горизонтальной, поэтому они являются поперечными волнами.

Если волны становятся очень мелкими (волны “ряби”) (их можно наблюдать в кювете с водой при возмущении поверхности жидкости иголкой) то “горб” стремится вернуть в положение равновесия другая сила – сила поверхностного натяжения, связанная с коэффициентом поверхностного натяжения.

В дальнейшем рассматриваются лишь поверхностные гравитационные волны, в распространении которых основное значение имеет сила земного притяжения.

Поверхностные волны с периодически повторяющимися характеристиками называются правильными или регулярными. Обычно ветровые волны или волны, вызываемые движением тел в жидкости, имеют трехмерный характер. Однако иногда, например, в случае волн зыби, картина волнового движения одинакова во всех плоскостях, совпадающих с направлением распространения волн, а образующие волновой поверхности – прямые линии. Такие волны называются плоскими.

Р

Рис. 10.2.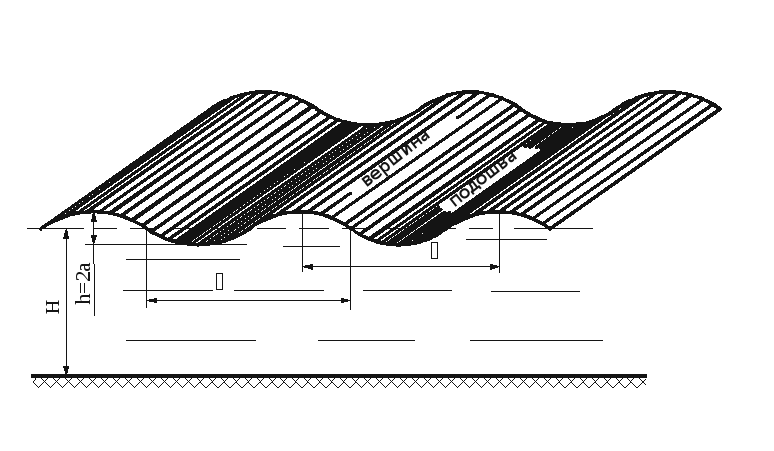

ассмотрим изображенное на рис. 10.2 сечение поверхности воды, покрытой правильными плоскими волнами. Характерными участками волнового профиля, образованного этим сечением, проведённым в плоскости распространения волн, являются вершины и подошвы волн, а основными характеристиками волн – их длина, высотаи период.

Длиной волны называется расстояние между соседними вершинами или подошвами, измеренное в направлении их распространения, а высотой волны – расстояние от её подошвы до вершины. Половина высоты правильных периодических волн называется их амплитудой.

Волны подразделяют на прогрессивные и стоячие. Профиль прогрессивных волн перемещается в пространстве; к ним относятся ветровые волны и волны, вызываемые движением тел в жидкости. Профиль стоячих волн не перемещается и лишь изменяет с течением времени свои ординаты в данной области пространства. Стоячие волны могут возникнуть, например, вследствие взаимодействия прогрессивных волн при их отражении от берегов и сооружений.

Скорость, с которой вершины прогрессивных волн перемещаются в пространстве, называют скоростью распространения волн или фазовой скоростью. Скоростьявляется скоростью перемещения профиля волн, и её не следует отождествлять со скоростью движения частиц, участвующих в волновом движении, которая обычно мала. Учитывая, что скорость распространения волн постоянна, её связь с длинойи периодомволн выражается формулой:

. (10.1)

Наблюдения показывают, что вязкость воды мало влияет на процессы распространения волн. Этим объясняется длительное существование морской зыби после окончания действия ветра.

Существенное влияние на характеристики волн оказывает их переход с глубокой воды на мелководный участок; происходит трансформация их профиля, возможно возникновение бурунов, а у побережья – волн прибоя.