
TETs_Sobolev
.pdf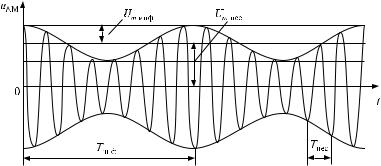
230 |
Г л а в а 6 |
Рис. 6.33. АМ-сигнал
Информационным сигналом uинф(t) может быть, например, речевой сигнал, т. е. напряжение, снимаемое с микрофона, представляющее собой реализацию случайного процесса. Однако для исследования свойств амплитудной модуляции удобно в качестве uинф(t) выбрать детерминированный тестовый сигнал, например гармоническое низкочастотное колебание.
Если uинф(t) = 0, т. е. информационный сигнал отсутствует, то имеет место высокочастотный гармонический сигнал (несущее колебание с постоянной амплитудой):
u(t) = Um нес cos !0t:
При наличии гармонического низкочастотного колебания
uинф(t) = Um инф cos Ωt |
|
АМ-сигнал описывается выражением |
|
uАМ(t) = (Um нес + Um инф cos Ωt) cos !0t: |
(6:23) |
Здесь Um нес, !0 = 2 =Tнес — амплитуда и частота высокочастотного сигнала (несущей); Um инф, Ω = 2 =Tинф — амплитуда и частота низкочастотного (информационного) сигнала.
Вынося в (6.23) Um нес за скобку, получаем |
|
uАМ(t) = Um нес(1 + m cos Ωt) cos !0t; |
(6:24) |
где m = Um инф=Um нес — глубина модуляции.
На рис. 6.33 приведён график сигнала, описываемого выражением (6.24) при m = 0;4.
При 0 6 m < 1 информационный сигнал не искажается. При m > 1 имеет место «перемодуляция», приводящая к искажению передаваемого информационного сигнала.
Выясним, из каких гармонических колебаний состоит АМ-сигнал при отсутствии искажений. Раскроем скобки в (6.24):
uАМ(t) = Um нес cos !0t + Um несm cos Ωt cos !0t =
Спектральный анализ периодических сигналов |
231 |
|||||
= Um нес cos !0t + |
1 |
mUm нес cos(!0 |
+ Ω)t + |
1 |
mUm нес cos(!0 |
Ω)t:(6:25) |
2 |
2 |
|||||
Следовательно, такой амплитудно-модулированный сигнал состоит из трёх гармонических колебаний:
несущей составляющей с частотой !0 и амплитудой Um нес;
верхней боковой составляющей с частотой !0 + Ω и амплитудой 0;5mUm нес;
нижней боковой составляющей с частотой !0 Ω и амплитудой 0;5mUm нес.
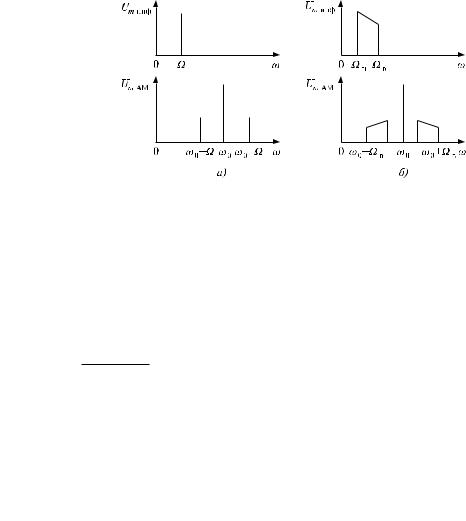
Графики амплитудных спектров гармонического (модулирующего) сигнала и соответствующего АМ-сигнала (при m = 0;75) изображены на рис. 6.34,a .
Рис. 6.34. Амплитудные спектры информационного сигнала и АМ-сигнала
Если спектр информационного (модулирующего) сигнала занимает некоторую полосу частот, то в спектре АМ-сигнала присутствуют две боковые полосы (рис. 6.34,b ). Ширина каждой боковой полосы равна ширине полосы информационного сигнала. Амплитуда и частота несущей составляющей неизменны во времени. Поэтому несущая не содержит передаваемой информации. Передаваемая информация заключена во временных´ изменениях огибающих боковых амплитудных спектров. Ширина всего спектра АМ-сигнала равна удвоенной верхней частоте информационного сигнала.
Отношение частот !0=Ω может выражаться как рациональным, так
ииррациональным числом. В первом случае uАМ(t) является периодическим сигналом, а во втором — квазипериодическим. Однако в обоих случаях спектр АМ-сигнала является дискретным, состоящим из трёх компонент.
Eсли спектр сигнала uинф(t) — дискретный, то спектр сигнала uАМ(t) тоже дискретный, в противном случае спектр сигнала uАМ(t) сплошной в пределах каждой боковой полосы частот.
232 |
Г л а в а 6 |
6.3.3. Задание для предварительного расчёта
6.3.3.1. Рассчитать и занести в табл. 6.5 отношения амплитуд третьей, пятой, седьмой и девятой гармоник к амплитуде первой гармоники в спектрах последовательностей треугольных и прямоугольных импульсов, воспользовавшись выражениями (6.21) и (6.22).
|
|
|
|
Таблица 6.5 |
|
Форма импульсов |
Способ расчёта |
Um3=Um1 |
Um5=Um1 |
Um7=Um1 |
Um9=Um1 |
в последовательности |
|
|
|
|
|
|
Теоретический |
|
|
|
|
Треугольная |
По результатам |
|
|
|
|
|
эксперимента |
|
|
|
|
|
Теоретический |
|
|
|
|
Прямоугольная |
По результатам |
|
|
|
|
|
эксперимента |
|
|
|
|
6.3.3.2. Рассчитать и занести в табл. 6.6 значения коэффициентов гармоник Kг для гармонического сигнала и для последовательностей импульсов треугольной и прямоугольной форм, воспользовавшись выражениями (6.21) и (6.22).
|
|
Таблица 6.6 |
Сигнал |
Способ расчёта |
Коэффициент гармоник Kг |
Гармонический |
Теоретический |
|
По результатам эксперимента |
|
|
|
|
|
Последовательность |
Теоретический |
|
треугольных импульсов |
По результатам эксперимента |
|
Последовательность |
Теоретический |
|
прямоугольных импульсов |
По результатам эксперимента |
|
6.3.3.3. Опираясь на выражение (6.25), рассчитать и занести в табл. 6.7 отношения амплитуд боковых составляющих к амплитуде несущей частоты в спектре АМ-сигнала при следующих значениях глубины модуляции m: 0,2; 0,5; 1,0; 1,5.
|
|
|
|
Таблица 6.7 |
Способ расчёта |
|
Отношение Um бок=Um нес |
||
|
при m = 0;2 |
при m = 0;5 |
при m = 1;0 |
при m = 1;5 |
Теоретический |
|
|
|
|
По результатам эксперимента |
|
|
|
|
6.3.4. Вопросы для самопроверки
1. Чем отличаются друг от друга амплитудные спектры последовательностей треугольных и прямоугольных импульсов?
Спектральный анализ периодических сигналов |
233 |
2.Что такое коэффициент гармоник и какие свойства сигнала он отражает?
3.Как связаны искажения переходной характеристики системы передачи с искажениями фронтов и вершин передаваемых прямоугольных импульсов?
4.Что такое амплитудная модуляция?
5.Какова цель амплитудной модуляции?
6.Что такое глубина амплитудной модуляции?
7.При каких значениях глубины амплитудной модуляции не происходит искажений информационного сигнала?
8.Какова структура и ширина спектра АМ-сигнала?
6.3.5. Задание для самостоятельного выполнения экспериментов на персональном компьютере
6.3.5.1.Провести сравнительное исследование спектров гармонического сигнала и последовательностей импульсов прямоугольной и треугольной форм (т. е. сигналов, изображённых на рис. 6.32).
6.3.5.2.Выяснить, как влияет на форму прямоугольных импульсов исключение из спектра сигнала высокочастотных и низкочастотных составляющих.
6.3.5.3.Изучить временн´ое и частотное представление сигнала амплитудной модуляции, а также выяснить влияние глубины модуляции и ширины спектра информационного сигнала на амплитудный спектр АМ-сигнала.
6.3.6. Порядок выполнения экспериментов
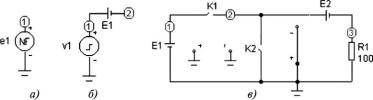
6.3.6.1.Сконструировать на рабочем поле редактора схему, изображённую на рис. 6.35,a, задав ЭДС источника e = 2;5 sin(2 106t) B. Получить и занести в отчёт график временн´ой зависимости гармонического напряжения на выходе источника и графики его амплитудного и фазового спектров. Определить значение коэффициента гармоник Kг и занести его в табл. 6.6.
6.3.6.2.Сконструировать на рабочем поле редактора схему, изображённую на рис. 6.35,b, обеспечив на её выходе напряжение, изменяющееся по закону треугольного сигнала (см. п. 6.3.7.4). Получить и
Рис. 6.35. Схемы, набираемые на рабочем поле редактора
234 |
Г л а в а 6 |
занести в отчёт график временн´ой зависимости напряжения на выходе схемы и графики его амплитудного и фазового спектров. Рассчитать и занести в табл. 6.5 значения отношений амплитуд высших гармоник к амплитуде первой гармоники. Рассчитать и занести в табл. 6.6 коэффициент гармоник. Сравнить полученные значения Umk=Um1 и Kг с соответствующими значениями, полученными в результате предварительного расчёта.
6.3.6.3. Сконструировать на рабочем поле редактора схему, изображённую на рис. 6.35,v, обеспечив на резисторе R1 напряжение, соответствующее одному периоду последовательности биполярных прямоугольных импульсов с максимальным значением 2,5 B и скважностью S = 2 (см. п. 6.3.7.5). Получить и занести в отчёт график временн´ой зависимости упомянутого напряжения и графики его амплитудного и фазового спектров. Рассчитать и занести в табл. 6.5 отношения амплитуд высших гармоник к амплитуде первой гармоники. Рассчитать и занести в табл. 6.6 коэффициент гармоник. Сравнить полученные значения Umk=Um1 и Kг с соответствующими значениями, полученными в результате предварительного расчёта.
Сравнить графики амплитудных спектров, а также значения коэффициента гармоник, полученные при выполнении пп. 6.3.6.1–6.3.6.3. Сделать и записать в отчёт вывод о том, как влияют на амплитудный спектр резкие изменения сигнала во времени.
6.3.6.4.Сконструировать на рабочем поле редактора схему, изображённую на рис. 6.35,a, задав ЭДС источника e = sin(2 106t) B. Получить и занести в отчёт графики амплитудного спектра и временн´ого представления одного периода напряжения на выходе источника.
6.3.6.5.Не меняя схему, повторить эксперимент, описанный в предыдущем пункте, при e = sin(2 106t) + 0;333 sin(2 3 106t) B.
6.3.6.6.Не меняя схему, повторить эксперимент, описанный в
п.6.3.6.4, при e = sin(2 106t) + 0;333 sin(2 3 106t) + 0;2 sin(25 106t) B.
6.3.6.7.Не меняя схему, повторить эксперимент, описанный в
п.6.3.6.4, при e = sin(2 106t) + 0;333 sin(2 3 106t) + 0;2 sin(25 106t) + 0;143 sin(2 7 106t) + 0;111 sin(2 9 106t) + 0;091 sin(2
11 106t) + 0;077 sin(2 13 106t) + 0;067 sin(2 15 106t) В. Сделать и записать в отчёт вывод о том, что в результате добавления высших спектральных составляющих формируются более крутые фронты импульсов.
Продолжая в рассматриваемом примере добавлять высшие гармоники с нулевыми фазами и с амплитудами, значение которых изменяется в соответствии с формулой 4Um=( (2n + 1)), где n = 0;1;2; :::, можно получить импульсы, сколь угодно близкие к прямоугольным.
Спектральный анализ периодических сигналов |
235 |
Исключение высших составляющих приводит к сглаживанию фронтов.
6.3.6.8.Повторить эксперимент, описанный в предыдущем пункте, предварительно исключив из выражения для ЭДС слагаемое sin(2 106t). Сделать и занести в отчёт вывод о том, что устранение первой гармоники искажает плоскую вершину импульса.
6.3.6.9.Сконструировать на рабочем поле редактора схему, изображённую на рис. 6.35,a, задав ЭДС источника e = 10[1 + 0;5 cos(2103t) cos(2 104)] B, т. е. обеспечив на его выходе АМ-сигнал со следующими значениями параметров: Ω = 2 103 рад/с, !0 = 2
104 рад/с, Um нес = 10 В, m = 0;5. Получить и занести в отчёт график временн´ого представления этого сигнала и график его амплитудного спектра. Сделать и занести в отчёт вывод о спектральном составе АМ-сигнала. Измерить амплитуды и частоты несущей и боковых составляющих. Определить ширину спектра АМ-сигнала. Занести полученные значения в отчёт.
6.3.6.10.Повторить эксперимент, описанный в предыдущем пун-
кте, установив предварительно новое значение несущей частоты !0 = 2 2;5 104 рад/с. Сделать и занести в отчёт вывод о том, как влияет на вид амплитудного спектра изменение значения несущей частоты. Определить и занести в табл. 6.7 отношение Um бок=Um нес и сравнить его со значением, полученным в результате предварительного расчёта.
6.3.6.11.Получить и занести в отчёт графики АМ-сигналов и графики соответствующих амплитудных спектров при следующих значениях глубины модуляции: 0,2, 1,0, 1,5. Сделать и занести в отчёт вывод о том, как влияет глубина модуляции на форму сигнала и форму его амплитудного спектра. Определить и занести в табл. 6.7 отношения Um бок=Um нес и сравнить их со значениями, полученными в результате предварительного расчёта. Сделать и занести в отчёт вывод о том, при каких значениях глубины модуляции возникают искажения информационного сигнала.
6.3.6.12.Получить и занести в отчёт график периодического сиг-
нала
uинф(t) = 4 cos(2 2 103t) + 5 sin(2 3 103t) +
+3 sin(2 4 103t) + 2соs(2 5 103t) В
играфик его амплитудного спектра.
6.3.6.13.Получить и занести в отчёт график АМ-сигнала
uАМ(t) = 10(1+0;4 cos(2 2 103t)+0;5 sin(2 3 103t)+0;3 sin(2 4 103t)+ + 0;2соs(2 5 103t)) cos(2 2;5 104t) В;
являющегося результатом амплитудной модуляции гармонического напряжения с амплитудой 10 B и частотой !0 = 2 2;5 104 рад/с
236 |
Г л а в а 6 |
периодическим сигналом, описанным в предыдущем пункте, а также график амплитудного спектра этого АМ-сигнала. Сделать и занести в отчёт вывод о спектральном составе АМ-сигнала. Измерить ширину его спектра и занести результат измерения в отчёт.
6.3.7. Методические указания
6.3.7.1.При выполнении исследований следует снимать опцию Auto Scale Ranges, а требуемые граничные значения диапазонов на полях выдаваемых графиков задавать в полях X Range и Y Range
окна Transient Analysis Limits.
6.3.7.2.При выполнении экспериментов по каждому пункту параметры процедуры анализа следует задавать в соответствии с табл. 6.8.
6.3.7.3.ЭДС источников в схемах, использующихся при выполнении пп. 6.3.6.1 и 6.3.6.4–6.3.6.13, следует описывать в окне Value или VALUE выражениями, составленными в соответствии с нотацией, принятой в алгоритмических языках. Например, при выполнении
п.6.3.6.1 ЭДС источника следует описать так: 2:5 sin(2 pi 1e6 t).
6.3.7.4.Для задания параметра v1 при выполнении п. 6.3.6.2 использовать имя TRIANGLE, а для задания E1 — значение 2.5.
|
|
|
|
|
|
|
Таблица 6.8 |
|
Пункт |
P |
X Exp- |
Y Exp- |
X |
Y |
Time |
Maximum |
|
|
|
ression |
ression |
Range |
Range |
Range |
Time Step |
|
|
|
|
|
|
|
|
|
|
|
1 |
T |
v(1) |
1e-6 |
3, -3 |
|
|
|
6.3.6.1 |
2 |
F |
HARM(v(1)) |
1e7 |
3 |
1u |
0.1u |
|
|
3 |
F |
PHASE(FFT(v(1))) |
1e7 |
180,-180 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
T |
v(2) |
1e-6 |
3, -3 |
|
|
|
6.3.6.2 |
2 |
F |
HARM(v(2)) |
1e7 |
2.5 |
1u |
0.1u |
|
|
3 |
F |
PHASE(FFT(v(2))) |
1e7 |
180,-180 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
T |
v(3) |
1e-6 |
3, -3 |
|
|
|
6.3.6.3 |
2 |
F |
HARM(v(3)) |
1e7 |
3.5 |
1u |
0.1n |
|
|
3 |
F |
PHASE(FFT(v(3))) |
1e7 |
180,-180 |
|
|
|
|
|
|
|
|
|
|
|
|
6.3.6.4 |
|
|
|
|
|
|
|
|
6.3.6.5 |
|
|
|
|
|
|
|
|
6.3.6.6 |
1 |
F |
HARM(v(1)) |
15e6 |
1.2, 0 |
1u |
0.1n |
|
6.3.6.7 |
2 |
T |
v(1) |
1e-6 |
1.3,-1,3 |
|
|
|
6.3.6.8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.3.6.9 |
1 |
T |
v(1) |
3m |
25,-25 |
|
|
|
6.3.6.10 |
5m |
0.1u |
||||||
2 |
F |
HARM(v(1)) |
3.5e4 |
10 |
||||
6.3.6.11 |
|
|
||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
6.3.6.12 |
1 |
T |
v(1) |
3m |
11,-10 |
5m |
0.1u |
|
2 |
F |
HARM(v(1)) |
3.5e4 |
10 |
||||
|
|
|
||||||
|
|
|
|
|
|
|
|
|
6.3.6.13 |
1 |
T |
v(1) |
3m |
25,-25 |
5m |
0.1u |
|
2 |
F |
HARM(v(1)) |
3.5e4 |
10 |
||||
|
|
|
||||||
|
|
|
|
|
|
|
|
Спектральный анализ периодических сигналов |
237 |
6.3.7.5. Функционирование ключа K1 при выполнении п. 6.3.6.3 следует описать так: T,0,0.5u, а ключа K2 так: T,0.5u. Для E1 нужно задать значение 5, а для E2 — значение 2.5.
6.3.8. Графики
В результате выполнения данной работы должны быть получены графики, представленные на рис. 6.36–6.50.
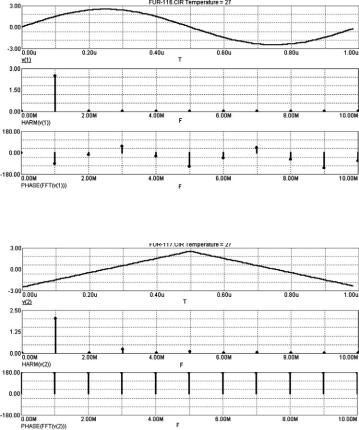
Рис. 6.36. Зависимости, полученные по заданию в п. 6.3.6.1
Рис. 6.37. Зависимости, полученные по заданию в п. 6.3.6.2
238 |
Г л а в а 6 |
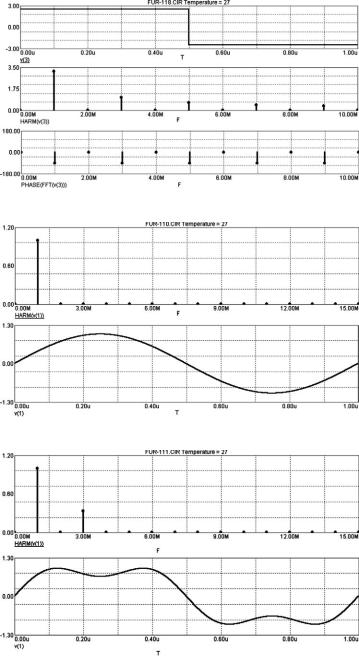
Рис. 6.38. Зависимости, полученные по заданию в п. 6.3.6.3
Рис. 6.39. Зависимости, полученные по заданию в п. 6.3.6.4
Рис. 6.40. Зависимости, полученные по заданию в п. 6.3.6.5
Спектральный анализ периодических сигналов |
239 |
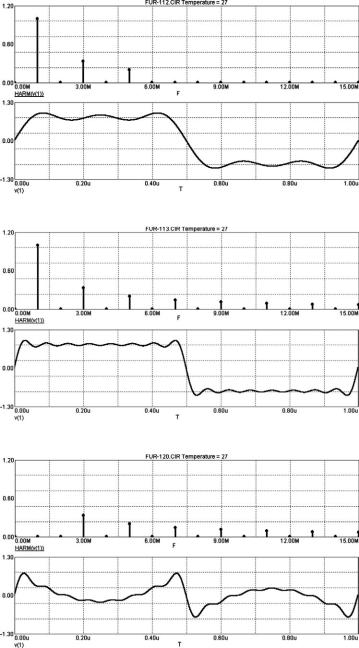
Рис. 6.41. Зависимости, полученные по заданию в п. 6.3.6.6
Рис. 6.42. Зависимости, полученные по заданию в п. 6.3.6.7
Рис. 6.43. Зависимости, полученные по заданию в п. 6.3.6.8
